4. Полигон и гистограмма.

Определение: Полигоном абсолютных частот называют ломаную линию, отрезки которой соединяют точки .

На оси абсцисс откладывают варианты 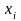, на оси ординат – соответствующие им частоты .

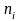Определение: Полигоном относительных частот называют ломаную линию, отрезки которой соединяют точки 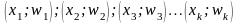. Для построения полигона относительных частот на оси OX откладывают варианты , а на оси ординат соответствующие им относительные частоты 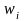. Точки 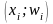соединяют прямыми и получают полигон относительных частот.

Полигон частот, постоенный по дискретному статистич ряду называется многоугольником распределения частот, который является анлогом многокугольника распределения вероятностей.

Заметим, что сумма ординат многоугольника распределения чатсот, как и у многоуг распределения вероятностей -= 1.

Определение: Гистограммой частот называют ступенчатую фигуру, состоящую из прямоугольников, основаниями служат интервалы длиной h, а высотами являются плотности частоты . Площадь гистограммы частот равна сумме всех частот, т. е. объёму выборки.

Определение: Гистограммой относительных частот называют ступенчатую фигуру, состоящую из прямоугольников с основаниями длиной h и высотами (плотность относительных частот). Площадь гистограммы равна сумме всех относительных частот, т. е. 1 служит для изображения интревального ряда.

Замечание: Полигон и гистограмма строятся для того, чтобы получить представление о форме функции плотности распределения.

Кумулята

Кумулята (кумулятивная кривая) –кривая накопленных частот . Для дискретного ряда представляет собой ломаную, соединияющ точку( xi, ni накл) или x I, wi накло) для интервального ряда ломаная начинается с точки асцисса которой равна началу первого интревала, а ордината накопленной чатстоте , равной нулю. Другие точки этой ломаной соответствует концам интревалов.

Рис. 6.3. Кумулята распределения домохозяйств по размеру

4. Рассчитаем накопленные частоты: Наколенная частота первого интервала рассчитывается следующим образом: 0 + 4 = 4, для второго: 4 + 12 = 16; для третьего: 4 + 12 + 8 = 24 и т.д.

Размер заработной платы руб в месяц Xi	Численность работников чел. fi	Накопленные частоты S
до 5000	4	4
5000 — 7000	12	16
7000 — 10000	8	24
10000 — 15000	6	30
Итого:	30	-

При построении кумуляты накопленная частота (частость) соответствующего интервала присваивается его верхней границе:

32. 2.Эмпирическая функция распределения.

Эмпирической функцией распределения (функцией распределения выборки) называют функцию 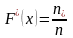, определяющ для каждого значения х относительную частоту события Х<х.

Итак по определунию , где

n – объём выборки

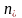– число наблюдений, при которых наблюдалось значение признака меньшее x.

Функцию распределения генеральной совокупности называют теоретической функцией распределения. Разница между ними следующая: Теоретическая функция распределения F(x) определяет вероятность события X<x, а эмпирическая – относительную частоту этого события.

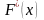- обладает теми же свойствами, что и F(x)

1. неубывающая

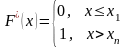
2)

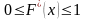
Эмпирическая функция распределения выборки служит для оценки теоретической функции распределения.

Итак, эмпирическая функция распределения выборки служит для оценки теорестич функции распределения генеральной совокупности.

26.Плотностью вероятности непрерывной двумерной СВ (X.Y)-вторая смешанная частная производная ее функции распределения, т.е. свойства:1) f(x.y)> или равно 0-неотрицательная. 2)Вер-сть попадания СВ в область D? P[X.Y]принадлежит D]= 3)F(x.y) может быть выражена через f(x.y) по формуле: F(x.y)= 4) Условные законы:В случае НСВ плотности вер-сти условных распределений f y(x) и f x(y) определяется по фор-ле: f(x/y)=fy(x)=f(x.y)/f₂(y) ,т.е. условная плотность вер-сть одной из одномерных состовляющих двумерной СВ=отношению ее совместной плотности к плотности вер-сти другой составляющей. Плотность совместного наступления f(x.y)=f₁(x)*f_x(y)=f₂(y)*f_y(x).Теорема умноженияплотностей распределения:умножая закон распределения одной из состаляющей на условный закон другой,мы найдем закон распределения системы СВ.

27. Начальным моментом порядка k, s двумерной случайной величины (Х,Y) называется математическое ожидание произведения X^k на Y^s:  α_k,s = M (X^kY^s) Для ДСВ:   для НСВ: , Центральным моментом порядка k, s двумерной случайной величины (Х, Y) называется математическое ожидание произведения (X – M(X))^k на (Y – M(Y))^s: μ_k,s = M((X – M(X))^k(Y – M(Y))^s).Для ДСВ:  Для НСВ: . Корреляционным моментом системы двух случайных величин называется второй смешанный центральный момент:K_xy = μ_1,1 = M((X – M(X))(Y – M(Y))).Для ДСВ   для НСВ:    Случайные величины   и   называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины   и   называются зависимыми.   Cov(x.y)=M[X*Y]-M[X]*M[Y], а коэфициент кореляции это ρ_xy=cov_xy/ σ(x) σ(y). Свойства:

лл

зависимость и независимость. Длч СВ независимых, если из них не зависит от того, какие возможные значения приняла другая СВ.

Теорема: для того, чтобы СВ х и у были независимыми, необходимо и достаточно ,чтобы функция распределения системы СВ (х,у) была равна произведению функции распределения её составляющих.

F(x,y) = F1(x) * F2(y)

В противном случае величины х и у называются зависимыми. Верно и обратное утверждение.

Дифференцируя дважды равенство по х и у :f(x,y)= f1(x)*f2(y)

Независимость двух СВ х и у также означает , то условные плотность вероятности совпадают с соответствующими «безусловными» плотностями.т.е.

f(x) * f(y) и f1(y)* f2(y)

Необходимые и достаточные условия независимости компонент х и у для дискретного и непрерывного случаев.

1. Х и у явл-ся независимыми дискретными СВ тогда и только тогда ,кгда для всех значений индексов I и j выпоняется

P_ij= P(X=x_i) * P(Y=y_j) = P_i*P_J

2. X и У явл-ся независим непрерывными СВ тогда и только тогда, когдпа f(x,y)= f₁(x)* f₂(y).

Переменнвые иногда могут быть связаны либо функциональной, либо статистической зависимостью, либо быть независимыми.

Строгая функц зависимость реализ реко.

Зависимость между двумя СВ наз-ся вероятностной (стохастической или статистической), если каждому значению одной из них соответствует определенное (условное) распределениедругой.

Ковариация и коэф корреляции

Ковариацией cov(х,у) (или корреляц момент)

СВ Х и У называется математич ожидание произведения отклонений этих величин от своих математ ожиданий, т. е.

cov_xy= M( (X – M(X)) (Y-M(Y) ) или cov_xy = M( (X-a_x) (y-a_y) )

из определения следует , что cov _xy= cov_yx

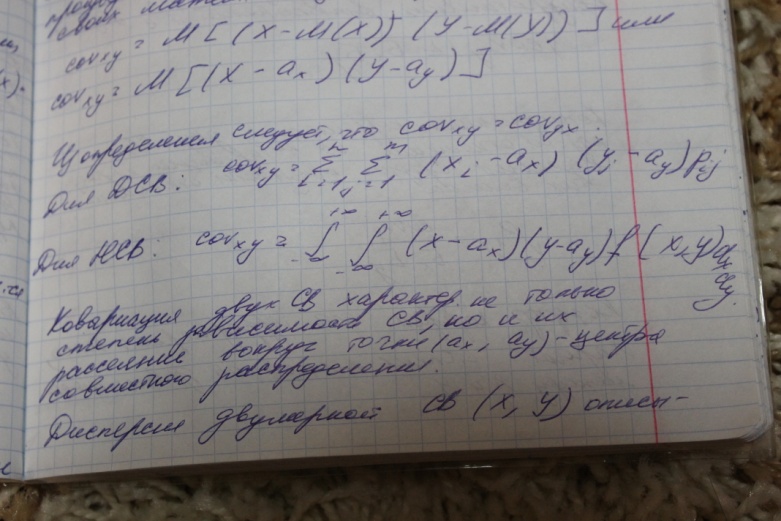
ковариация двух Св характер не толко степень зависимости СВ, но и их рассеяние вокруг точки (а_х, а_у)- центра совместн распределения.

Дисперсия двумерной Св (Х,У)называется ковариационной матрицей

(формула из фотки)

Св-ва ковариации случ величин:

1. Ковар двух независимых СВ= 0.

2. Ковариация двух СВ равна математич ожиданию их произведения произведения математичес ожиданий, т.е. cov _xy= M( XY) – M(X)*M(Y)

3. Ковариация двух СВ по абсолютной величине не происходит произведения их средних квадратических отклон, т.е

(формула из фотки)

Коэффициентомкорреляции двух СВ называется отношение их ковариации к произведению средних квадатич отклонений этих величин

(формула из фотки)

Коэффициент коорел есть безразмерной величин , характ степень линейной зависимостью между Х и У.

Их определения следует, что ρ_ху = ρ_yx= ρ

Свойства коэф корреляции:

1. Коэф корреляции принимает значение на отрезке (-1,+1) ,т.е. -1≤ρ≤+1.

2. Если коэф корреляции двух СВ (по абсол величине) единице, то между этими СВ существует линейная функц зависимость.

3. Если СВ независимы, то их коэф корреляциих = 0, т. е. ρ=0

Две Св наз-ся некореелир, если коэф корреляции = 0.

Таким образом из независим СВ следует их некореллир.

В частности, если Y= aX+ b, то g=±1

Свойства:

1. Для некорр СВ: M(X*Y) = M(X)*M(Y)

2. D(X+Y)= D(X) + D(Y) + 2 cov_xy

3. Для некор Св: D(X+Y) = D(X) + D(Y)

33.Среднеарифметическое-е  , свойства :1.Средняя арифметическая постоянной равна самой постоянной.2. Если все варианты увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз: 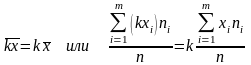3. Если все варианты увеличить (уменьшить) на одно и то же число, то средняя арифметическая увеличится (уменьшится) на то же число: 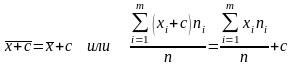.4. Средняя арифметическая отклонений вариантов от средней арифметической равна нулю:

.5. Средняя арифметическая алгебраической суммы нескольких признаков равна такой же сумме средних арифметических этих признаков:

.

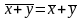
Выборочная дисперсия   – это смещенная оценка генеральной дисперсии; поэтому в качестве оценки генеральной дисперсии берут исправленную выборочную дисперсию  Для оценки среднего квадратичного отклонения -среднее линейное отклонение. -размах вариации. -коэффициент вариации.

Вариационный размах – это разность максимального и минимального значений статистического ряда: R= x_max –x_min.

Наибольший интерес представляют меры вариации (рассеяния) наблюдений вокруг средних величин.

Средним линейным отклонением статистического ряда называется средняя арифметическая абсолютных величин отклонений вариантов от их средней:

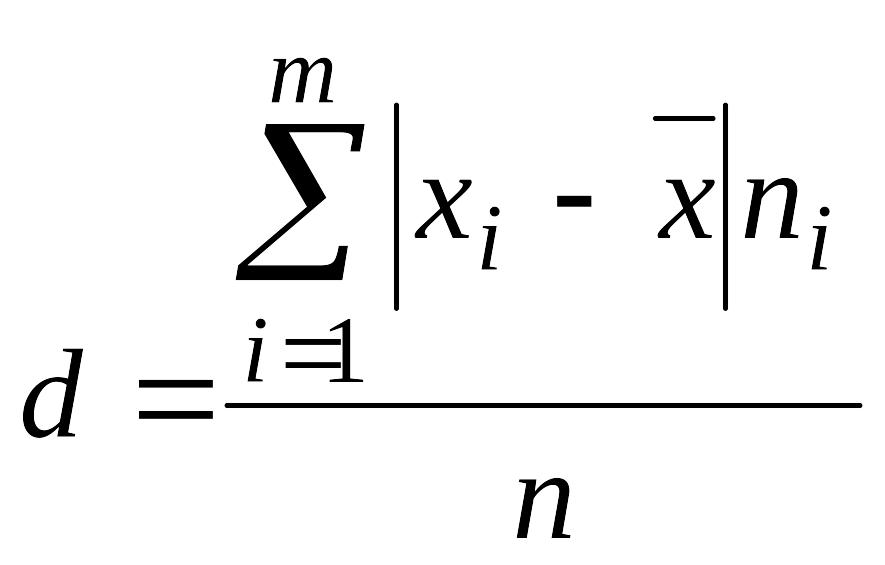
Выборочной дисперсией s² статистического ряда называется средняя арифметическая квадратов отклонений вариантов от их средней арифметической:

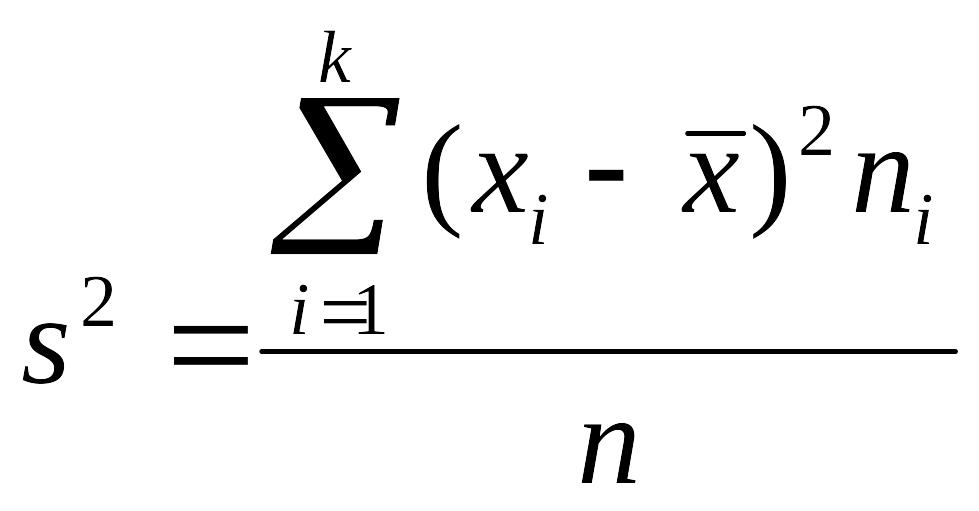или .

Для несгруппированного ряда (n_i=1): .

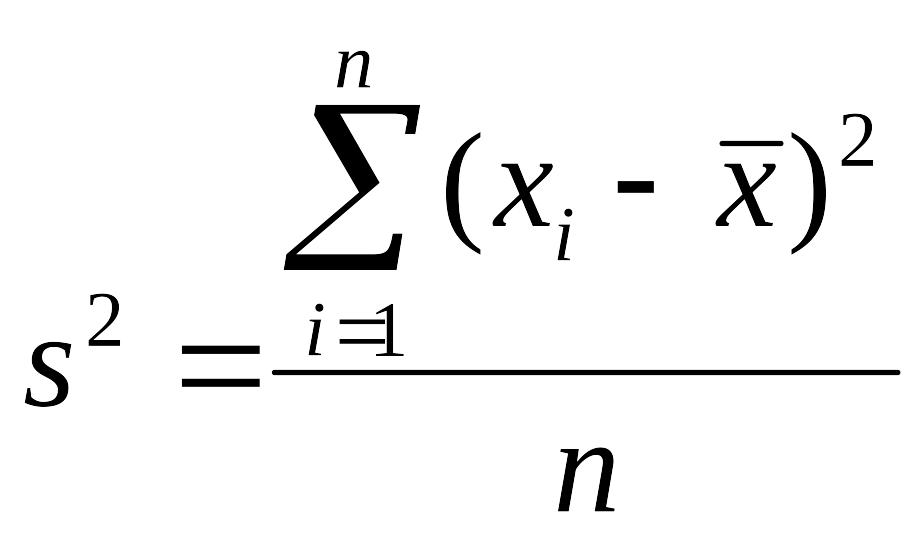Среднее квадратическое отклонение (стандартным отклонением) s статистического ряда – арифметическое значение корня квадратного из выборочной дисперсии:

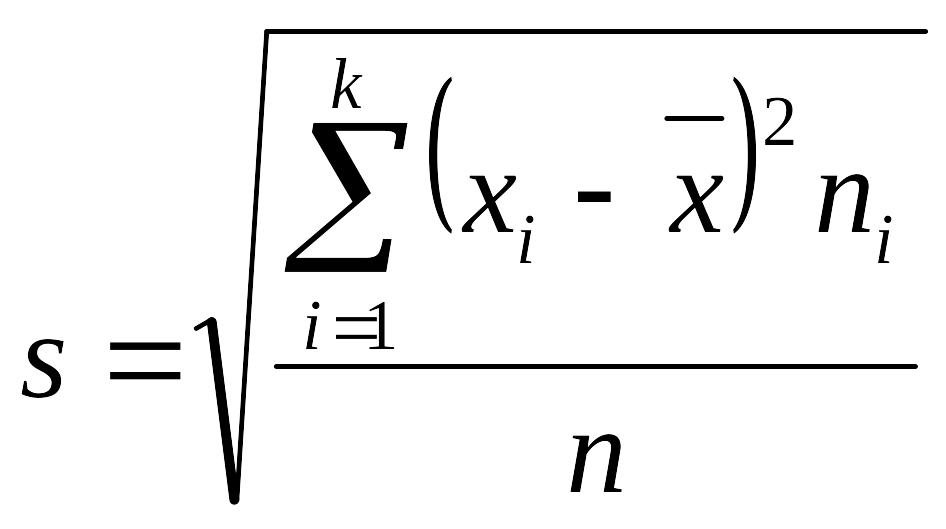или .

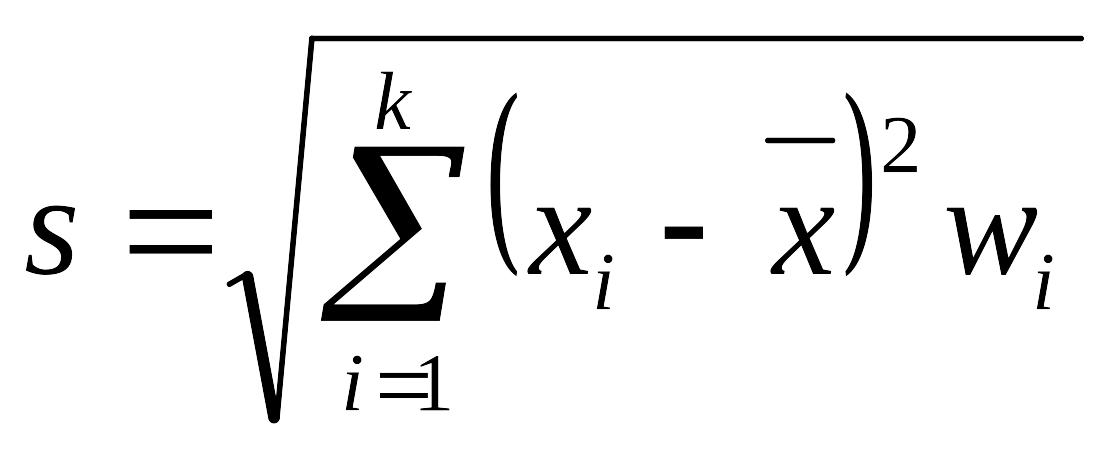Размерность стандартного отклонения в отличие от размерности дисперсии совпадает с единицами измерения варьирующего признака, поэтому в практической статистике для того, чтобы охарактеризовать рассеяние признака используют обычно стандартное отклонение, а не дисперсию.