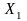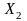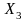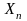28. Линейная регрессия.Пусть X и Y двумерной СВ (Х и У) линейно зависимы и одну из них можно представить как линейную функцию другой y =(волнис) g(X)= α+βX.Для определения параметров α, β применяется метод наименьших квадратов( МНК). Функция g(X) называют среднеквадратичной регрессией Y на X. Она является наилучшим приближением Y в смысле МНК, если М(У- g(Х))² => min. Рассмотрим функцию F(α,β)= M⁽Y – (αX+β))^2. На основании необходимого условия существования экстремум функции 2-ух переменных ( вставка формулы )

Коэффициент вставка формулы называется коэффициент регрессии Y На Х.

Прямая вида вставка формулы

Называется линейной средней квадратич регрессией У на Х.

Подставив координаты стац точки (α,β) в равенство F (α,β) M(Y- (αX +β))²

Получим F (α,β) = ҕ²y( 1 – p²) Эта велична называется остаточной дисперсией У относительно Х и характеризует величину ошибки, допускаемой при замене Х на g(X)= α+βx.Сл-но: при ρ= ±1 У и Х связано линейной функциональной зависимостью.

Аналогично получается прямая среднеквадратичная регрессии Х на У:

И остат дисперсии Х относительно У. При ρ = ±1 обе прямые регрессии совпадают.

Решив систему из уравнений: вставить

Найдем точку пересечения прямых регрессий – точку с координатами а_х a_y – центры совместного распределения величины Х и У.

Двухмерный норм закон распределения.

Двумерный нормальный закон распределения.. Систему случайных величин можно интерпретировать как случайную точку на плоскости. Нормальный закон распределения для системы (Х,У) называется двумерным нормальным законом распределения и имеет плотность вероятности

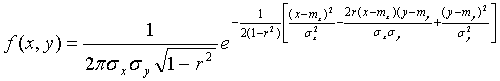
где  - математические ожидания соответственно случайных величин Х и У,  - средние квадратические отклонения этих величин, r – коэффициент корреляции Х и У. поверхность f(x,y) имеет вид

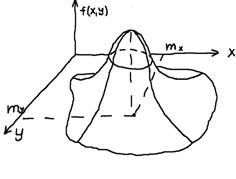
Таким образом, двумерный норм закон распределения определ 5 параметрами: а_х а_у- матем ожидание, - среднее квадратич отклонение, r – коэф коррел Х и У.

Числовые характер СВ Х и У:

1)М(Х)= ∫(вверху +∞, внизу- ∞) ∫(вверху +∞, внизу- ∞) х f_n( х,у) d_xd_{y =} а_х

₂₎ M (Y) ∫(вверху +∞, внизу- ∞) ∫(вверху +∞, внизу- ∞) y f_n( х,у) d_xd_{y =}a_y

Двумерный  нормальный закон распределения имеет, например, точка попадания снаряда из орудия, которое хорошо пристреляно по цели имеющей координаты .

Если случайные величины независимы, то r=0 и функция плотности вероятности f(x,y) имеет вид

 а ,

что соответствует упомянутому нами свойству систем независимых случайных величин (7).

Используя формулу (6) и f(x,y) можно вычислить вероятность попадания ХУ в любую область плотности. Особенно просто это сделать, если Х и У независимы, а область представляет собой прямоугольник со сторонами параллельными осям координат.

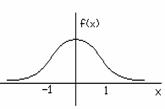
Выводы:

1. Линейная регрессия М_у( X ) и М_х(Y) нормально распределенных СВ и прямые линий, т.е нормальные регрессии У по Х и Х по У всегда линейны.

2. D_y(X) и D_x( У) ҕ_y(X) и ҕ_х(Y) – постоянны и независят от значений Y или Х – гомоскедастичность или равноизменчивость условных нормальных распределений и имеет существенное значение в статист анализе.

29. Сущность закона больших чисел..

Закон больших чисел – это обобщённое название нескольких теорем, из которых следует, что при неограниченном увеличении числа испытаний, среднее значение этих величин стремится к некоторым

2. Неравенство Чебышева.

Неравенство Чебышева справедливо для дискретных и непрерывных случайных величин. Пусть у нас есть дискретная случайная величина, заданная рядом распределения.

X				…
P				…

Требуется оценить вероятность того, что отклонение случайной величины от её математического ожидания не превышает по абсолютной величине положительного числа .

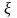Теорема (неравенство Чебышева). Для произвольной случайной величины X с математическим ожиданием a=M(X) и дисперсией 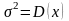, для любого 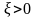справедливо равенство

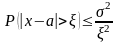(1)

Учитывая, что события 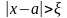и противоположны, неравенство Чебышева можно записать и в другой форме:

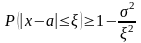(2)

Из неравенства Чебышева следует – чем меньше D(x), тем меньше вероятность отклонения. Неравенство Чебышева применимо для любых случайных величин. В форме (1) оно устанавливает верхнюю границу, а в форме (2) – нижнюю границу вероятности рассматриваемого события.

Запишем неравенство Чебышева в форме (2) для случайной величины Х, имеющей биномиальный закон распределения с математическим ожиданием а=М(Х)=np и дисперсией D(X)=npq.

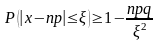
В основном неравенство Чебышева имеет теоретическое значение для теорем.

Пример. Средний расход воды на ферме составляет 1000л. в день, а среднее квадратическое отклонение этой случайной величины не превышает 200л. Оценить вероятность того, что расход воды на ферме в любой выбранный день не превзойдет 2000л.

Решение. Пусть Х – расход воды на ферме. По условию 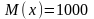. Дисперсия 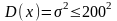. Так как границы интервала симметричны относительно математического ожидания , то для оценки вероятности искомого события применим неравенство Чебышева:

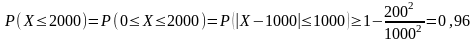, т.е. не менее, чем 0,96.

3.Теоремы Чебышева и Бернулли.

Теорема Чебышева: Пусть имеем достаточно большое число независимых случайных величин 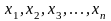дисперсия каждой из которых не превышает одного и того же постоянного числа, то для любого сколь угодно малого положительного , вероятность неравенства будет как угодно близка к 1.

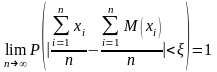
Пусть испытания независимы и проводятся в одинаковых условиях. Для частного случая, когда математические ожидания случайных величин одинаковы

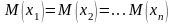,тогда

, тогда

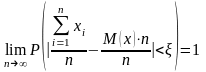
или 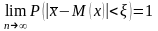, где 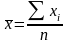- среднее арифметическое.

Смысл этого выражения в том, что начиная с некоторого момента для любого даже сколь угодно малого числа >0 будет верно неравенство 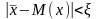т.е. 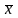обладает свойством устойчивости.

Терема Чебышева имеет большое практическое значение. Она позволяет, используя среднее арифметическое, получить представление о величине математического ожидания и наоборот.

Так, проводя какие-нибудь измерения, можно получить большое число результатов измерения, среднее арифметическое которых по теореме Чебышева будет мало отличаться от истинного значения параметра.