Угол между плоскостями. Условия параллельности и перпендикулярности плоскостей.

 

 Если две плоскости (α₁ и α₂) заданы общими уравнениями вида:

  A₁x+B₁y+C₁z+D₁=0   и   A₂x+B₂y+C₂z+D₂=0,

то очевидно, что угол между ними равен углу между их нормалями, то есть между векторами n₁={A₁,B₁,C₁) и n₂={A₂,B₂,C₂). Из формулы (5.6) получаем, что косинус угла между плоскостями  α₁ и α₂  равен

                                                                  (8.4)

Условие параллельности плоскостей заключается в параллельности нормалей:

                                                                                                         (8.5)

а условие перпендикулярности плоскостей – в перпендикулярности нормалей или равенстве нулю их скалярного произведения:

                    A₁A₂ + B₁B₂ + C₁C₂ = 0.                                                                       (8.6)

 

       Выведем еще несколько уравнений плоскости. Пусть плоскость проходит через точки М₁(х₁, у₁, z₁), M₂(x₂, y₂, z₂) и M₃(x₃, y₃, z₃), не лежащие на одной прямой. Тогда векторы  М₁М₂={x₂ -x₁, y₂ - y₁, z₂ - z₁}, М₁М₃={x₃ - x₁, y₃ - y₁, z₃ - z₁} и М₁М={x - x₁, y - y₁, z - z₁}, где М(x, y, z) – произвольная точка плоскости, компланарны. Следовательно, их смешанное произведение равно нулю. Используя координатную запись смешанного произведения, получаем:

                                                                                  (8.7)

Это уравнение, которому удовлетворяют координаты х, у, z любой точки, лежащей на искомой плоскости, является уравнением плоскости, проходящей через три данные точки.

   Способом, аналогичным изложенному в лекции 7, можно получить нормальное уравнение плоскости:

                                                                                 (8.8)

где р – длина перпендикуляра ОР, опущенного из начала координат на плоскость, а cosα, cosβ, cosγ – направляющие косинусы нормали к этой плоскости. При этом расстояние от любой точки А пространства до данной плоскости определяется по формуле:

                    ,                                                       (8.9)

где x₀,y₀,z₀ – координаты рассматриваемой точки А. Подмодульное выражение в формуле (8.9) называется отклонением точки А от плоскости и принимает положительные значения, если А и начало координат лежат по разные стороны от плоскости, и отрицательные, если эти две точки лежат по одну сторону от плоскости. Нормальное уравнение получается из общего уравнения плоскости в результате деления его на нормирующий множитель  знак которого противоположен знаку D.

Доказательства всех сформулированных утверждений полностью аналогичны исследованию нормального уравнения прямой на плоскости, рассмотренного в лекции 7.

 

                       Прямая в пространстве.

    Первая возможность составить уравнения прямой в пространстве – представить эту прямую как пересечение двух непараллельных плоскостей, заданных уравнениями

A₁x+B₁y+C₁z+D₁=0   и   A₂x+B₂y+C₂z+D₂=0, где коэффициенты A₁,B₁,C₁ и A₂,B₂,C₂ не пропорциональны:

 

                         A₁x+B₁y+C₁z+D₁=0                                                                   (8.10)

                         A₂x+B₂y+C₂z+D₂=0.

Однако при решении многих задач удобнее пользоваться другими уравнениями прямой, содержащими в явной форме некоторые ее геометрические характеристики.

  Составим уравнения прямой, проходящей через точку М₀(x₀,y₀,z₀) параллельно вектору a={l,m,n}.

Определение 8.1. Любой ненулевой вектор, параллельный данной прямой, называется ее направляющим вектором.

   Для любой точки М(x,y,z), лежащей на данной прямой, вектор М₀М = {x - x₀,y - y₀,z - z₀) коллинеарен направляющему вектору а. Поэтому имеют место равенства:

                                                                                         (8.11)

называемые каноническими уравнениями  прямой в пространстве.

В частности, если требуется получить уравнения прямой, проходящей через две точки:

М₁(х₁, у₁, z₁) и M₂(x₂, y₂, z₂), направляющим вектором такой прямой можно считать вектор М₁М₂ = {x₂ – x₁, y₂ - y₁, z₂ - z₁}, и уравнения (8.11) принимают вид:

                       -                                                              (8.12)

-          уравнения прямой, проходящей через две данные точки.

Если же принять каждую из равных дробей в уравнениях (8.11) за некоторый параметр t, можно получить так называемые параметрические уравнения прямой:

                            .                                                                                  (8.13)

     Для того, чтобы перейти от уравнений (8.10) к каноническим или параметрическим уравнениям прямой, требуется найти направляющий вектор этой прямой и координаты любой точки, принадлежащей ей. Направляющий вектор прямой ортогонален нормалям к обеим плоскостям, следовательно, он коллинеарен их векторному произведению. Поэтому в качестве направляющего вектора можно выбрать [n₁n₂] или любой вектор с пропорциональными координатами. Чтобы найти точку, лежащую на данной прямой, можно задать одну ее координату произвольно, а две остальные найти из уравнений (8.10), выбрав их так, чтобы определитель из их коэффициентов не равнялся нулю.

 

      Угол между прямыми. Угол между прямой и плоскостью.

 

Угол между прямыми в пространстве равен углу между их направляющими векторами. Поэтому, если две прямые заданы каноническими уравнениями вида

   и      косинус угла между ними можно найти по формуле:

                  .                                                   (8.14)

Условия параллельности и перпендикулярности прямых тоже сводятся к соответствующим условиям для их направляющих векторов:

   -  условие параллельности прямых,                                     (8.15)

  -   условие перпендикулярности прямых.                (8.16)

   Угол φ между прямой, заданной каноническими уравнениями

                                                                                                                                                           и плоскостью, определяемой общим уравнением 

                            Ax + By + Cz + D = 0,                                                                                                                                                                                                          можно рассматривать как дополнительный к углу ψ между направляющим вектором прямой и нормалью к плоскости. Тогда

                                                        (8.17)   

Условием параллельности прямой и плоскости является при этом условие перпендикулярности векторов n и а:

                     Al + Bm + Cn = 0,                                                                                (8.18)

а условием перпендикулярности прямой и плоскости – условие параллельности этих векторов:   A/l = B/m = C/n.                                                                                       (8.19)

В 38. Понятие линейной зависимости и линейной независимости системы векторов. Линейное пространство. Размерность пространства, базис.

Рассмотрим набор из p n-мерных векторов, обозначим их следующим образом  . Составим линейную комбинацию этих векторов и произвольных чисел   (действительныхили комплексных):  . Отталкиваясь от определения операций над n-мерными векторами, а так же свойств операций сложения векторов и умножения вектора на число, можно утверждать, что записанная линейная комбинация представляет собой некоторый n-мерный вектор  , то есть,  .

Определение.

Если линейная комбинация   может представлять собой нулевой вектор тогда, когда среди чисел   есть хотя бы одно, отличное от нуля, то система векторов   называется линейно зависимой.

Определение.

Если линейная комбинация   представляет собой нулевой вектор только тогда, когда все числа   равны нулю, то система векторов   называется линейно независимой.

На основании данных определений, сформулируем и докажем свойства линейной зависимости и линейной независимости системы векторов.

1. Если к линейно зависимой системе векторов   добавить несколько векторов, то полученная система будет линейно зависимой.

Доказательство.

Так как система векторов   линейно зависима, то равенство   возможно при наличии хотя бы одного ненулевого числа из чисел  . Пусть  .

Добавим к исходной системе векторов еще s векторов  , при этом получим систему  . Так как   и  , то линейная комбинация векторов этой системы вида   представляет собой нулевой вектор, а  . Следовательно, полученная система векторов является линейно зависимой.

2. Если из линейно независимой системы векторов   исключить несколько векторов, то полученная система будет линейно независимой.

Доказательство.

Предположим, что полученная система линейно зависима. Добавив к этой системе векторов все отброшенные векторы, мы получим исходную систему векторов. По условию – она линейно независима, а в силу предыдущего свойства линейной зависимости она должна быть линейно зависимой. Мы пришли к противоречию, следовательно, наше предположение неверно.

3. Если в системе векторов   есть хотя бы один нулевой вектор, то такая система линейно зависимая.

Доказательство.

Пусть вектор   в этой системе векторов является нулевым. Предположим, что исходная система векторов линейно независима. Тогда векторное равенство   возможно только тогда, когда  . Однако, если взять любое  , отличное от нуля, то равенство   все равно будет справедливо, так как  . Следовательно, наше предположение неверно, и исходная система векторов линейно зависима.

4. Если система векторов   линейно зависима, то хотя бы один из ее векторов линейно выражается через остальные. Если система векторов   линейно независима, то ни один из векторов не выражается через остальные.

Доказательство.

Сначала докажем первое утверждение.

Пусть система векторов   линейно зависима, тогда существует хотя бы одно отличное от нуля число   и при этом верно равенство  . Это равенство можно разрешить относительно  , так как  , при этом имеем Следовательно, вектор   линейно выражается через остальные векторы системы  , что и требовалось доказать.

Теперь докажем второе утверждение.

Так как система векторов   линейно независима, то равенство   возможно лишь при  .

Предположим, что какой-нибудь вектор системы   выражается линейно через остальные. Пусть этим вектором является  , тогда  . Это равенство можно переписать как  , в его левой части находится линейная комбинация векторов системы, причем коэффициент перед вектором   отличен от нуля, что указывает на линейную зависимость исходной системы векторов. Так мы пришли к противоречию, значит, свойство доказано.

Из двух последних свойств следует важное утверждение: если система векторов содержит векторы   и  , где   – произвольное число, то она линейно зависима.

Векторное пространство  называется n-мерным, если в нем можно найти n линейно независимых векторов, но больше, чем n линейно независимых векторов оно не содержит.

Размерность пространства – это максимальное число содержащихся в нем линейно независимых векторов.

Размерность пространства  условимся обозначать через dim.

Например, размерность множества всех плоских векторов равна 2, размерность множества пространственных векторов равна 3.

Пространство, имеющее конечную размерность, называется конечномерным. Пространство, в котором можно найти сколь угодно много линейно независимых векторов, называется бесконечномерным.

Совокупность n линейно независимых векторов n- мерного векторного пространства  называется его базисом.

Теорема 1. Каждый вектор  линейного n- мерного пространства  можно представить, и притом единственным способом, в виде линейной комбинации векторов базиса.

Доказательство. Пусть  - произвольный базис пространства  и . Так как любые n+1 векторов пространства  линейно зависимы, то зависимы, в частности, и векторы , т.е. существуют не равные одновременно нулю числа , такие, что

.

При этом , в противном случае хотя бы одно из чисел  было бы отлично от нуля, и вектора  были бы линейно зависимы. Следовательно, .

Полагая , будем иметь .

Это представление  через  единственно. Доказывается от противного. Числа  называются координатами вектора  в базисе .

Теорема 2. Если  - линейно независимые векторы пространства  и любой вектор  линейно выражается через , то эти векторы образуют базис в .

Доказательство. Векторы , по условию, линейно независимы. Покажем, что в пространстве  нет более чем n линейно независимых векторов. Выберем произвольные  векторов из : . По условию, каждый из них можно линейно выразить через :

Рассмотрим матрицу:

.

Так как число строк этой матрицы равно n, то ее ранг не больше, чем n, и значит, среди ее столбцов имеется не более, чем n линейно независимых. Но так как m>n, то m столбцов этой матрицы линейно зависимы. Следовательно, линейно зависимы и векторы . Итак, пространство  n – мерно и  - его базис.

Пусть в пространстве  имеется два базиса:  и .

Первый условимся называть старым базисом, второй – новым. Каждый из векторов нового базиса, по Теореме 5.1, можно линейно выразить через векторы старого базиса:

(5.1)

Новые базисные векторы получаются из старых с помощью матрицы

При этом коэффициенты их разложений по старым базисным векторам образуют столбцы этой матрицы. Матрица  называется матрицей перехода от базиса  к базису .

Определитель матрицы  не равен нулю, так как в противном случае ее столбцы, а следовательно и векторы , были бы линейно зависимы.

Обратно, если , то столбцы матрицы линейно независимы, и следовательно векторы , получающиеся из базисных векторов  с помощью матрицы , линейно независимы и значит образуют некоторый базис. Таким образом, матрицей перехода может служить любая квадратная матрица порядка n с отличным от нуля определителем.

Рассмотрим теперь, как связаны между собой координаты одного и того же вектора в старом и новом базисах. Пусть  в старом базисе и  - в новом. Подставляя в последнее равенство вместо  их выражение из (5.1), получим, что

        Таким образом, старые координаты вектора  получатся из новых его координат с помощью той же матрицы , только коэффициенты соответствующих разложений образуют строки этой матрицы.

В 39. Ранг матриы, методы его вычисления. Базисный минор.

Рангом r(A) матрицы A называется самый большой порядок, для которого существуют отличные от нуля миноры. Если ранг матрицы A равен r, то это означает, что в матрице A имеется отличный от нуля минор порядка r, но всякий минор порядка, большего чем r равен нулю. Имеет место

Теорема о ранге матрицы: Ранг r матрицы A равен максимальному числу линейно независимых столбцов (строк).

Лемма. Максимальное число линейно независимых строк в матрице равно максимальному числу линейно независимых столбцов в этой матрице.

Если каждый элемент матрицы равен нулю, то ранг такой матрицы, по определению, считают равным нулю. Если r(A)=r(B), то матрицы A и B называются эквивалентными. В этом случае пишется: A ~B.

 Ранг матрицы не изменяется от элементарных преобразований.

Под элементарными преобразованиями понимается:

А) замена строк столбцами, а столбцов - соответствующими строками;

Б) перестановка строк (столбцов) матрицы;

В) вычеркивание ряда (строки или столбца), все элементы которого равны нулю;

Г) умножение какого-либо ряда (строки или столбца) на число, отличное от нуля

Д) прибавление к элементам одного ряда соответствующих элементов другого параллельного ряда.

Эквивалентные преобразования не меняют ранга матрицы; переходя от матрицы A к матрице A₁ и т.д., с помощью эквивалентных преобразований, мы получаем, вообще говоря, разные матрицы, но эти матрицы имеют один и тот же ранг. Действительно, сравнивая эквивалентные преобразования матрицы со свойствами определителя видим, что определитель, не равный нулю, и в ходе эквивалентных преобразований остается отличным от нуля.

Если матрица n -го порядка имеет вид верхней треугольной матрицы, то её определитель равен произведению элементов, стоящих на главной диагонали. Это свойство используется при вычислении ранга матрицы: необходимо привести матрицу к верхней треугольной и тогда, выделив соответствующий определитель, найдем, что ранг матрицы равен числу элементов главной диагонали, отличных от нуля (или порядку найденного максимального минора M≠0).

Методы вычисления рангов

1. метод окаймления миноров

2. применение элементарных преобразований матрицы и использование следующих утверждений

а)Ранг ступенчатой матрицы равен количеству её ненулевых строк.

б)Элементарные преобразования матрицы не изменяют её ранг

В 40. Однородные СЛАУ. Условие нетравиальной совместности линейной однородной системы. Фундаментальная система решений однородной системы уравнений

Рассмотрим систему m линейных алгебраических уравнений относительно n неизвестных  x₁ , x₂ , ..., x_n :

Решением системы называется совокупность n значений неизвестных x₁=x'₁ , x₂ =x'₂ , ..., x_n=x'_n , при подстановке которых все уравнения системы обращаются в тождества.

Система линейных уравнений может быть записана в матричном виде:

где A — матрица системы, b — правая часть, x — искомое решение, A_p — расширенная матрица системы:

  .

Система, имеющая хотя бы одно решение, называется совместной; система, не имеющая ни одного решения — несовместной.

Однородной системой линейных уравнений называется система, правая часть которой равна нулю:

Матричный вид однородной системы: Ax=0.

Однородная система в с е г д а  с о в м е с т н а, поскольку любая однородная линейная система имеет по крайней мере одно решение:

x₁=0 , x₂=0 , ..., x_n=0.

Если однородная система имеет единственное решение, то это единственное решение — нулевое, и система называется тривиально совместной.

 Если же однородная система имеет более одного решения, то среди них есть и ненулевые и в этом случае система называетсянетривиально совместной.

Для того чтобы при m=n для нетривиальной совместности системы необходимо и достаточно, чтобы определитель матрицы системы был равен нулю.

 

ПРИМЕР 1. Нетривиальная совместность однородной системы линейных уравнений с квадратной матрицей.

 

Применив к матрице системы алгоритм гауссова исключения, приведем матрицу системы к ступенчатому виду

.

Число r ненулевых строк в ступенчатой форме матрицы называется рангом матрицы,обозначаем  r=rg(A)  или r=Rg(A).

Справедливо следующее утверждение.

Для того, чтобы однородная система была нетривиально совместна, необходимо и достаточно, чтобы ранг r матрицы системы был меньше числа неизвестных n.

 

Если однородная система нетривиально совместна, то она имеет бесконечное множество решений, причем линейная комбинация любых решений системы тоже является ее решением.  Кроме того, среди бесконечного множества решений однородной системы можно выделить ровно n-r линейно независимых решений.  Совокупность n-r линейно независимых решений однородной системы называетсяфундаментальной системой решений. Любое решение системы линейно выражается через фундаментальную систему. Таким образом, если ранг r матрицы A однородной линейной системы Ax=0  меньше числа неизвестных n и векторы e₁ , e₂ , ..., e_n-r  образуют ее фундаментальную систему решений (Ae_i =0, i=1,2, ..., n-r), то любое решение x системы Ax=0 можно записать в виде

x=c₁ e₁ + c₂ e₂ +  ... + c_n-r e_n-r ,

где c₁ , c₂ , ..., c_n-r — произвольные постоянные. Записанное выражение называется общим решением однородной системы.

Исследовать однородную систему   — значит установить, является ли она нетривиально совместной, и если является, то найти фундаментальную систему решений и записать выражение для общего решения системы.

Исследуем однородную систему методом Гаусса.

Пусть

матрица исследуемой однородной системы, ранг которой r< n.

Такая матрица приводится Гауссовым исключением к ступенчатому виду

.

Соответствующая эквивалентная система имеет вид

Отсюда легко получить выражения для переменных x₁ , x₂ , ..., x_r через x_r+1 , x_r+2 , ..., x_n . Переменные  x₁ , x₂ , ..., x_r  называют базисными переменными, а переменные x_r+1 , x_r+2 , ..., x_n —свободными переменными.

Перенеся свободные переменные в правую часть, получим формулы

которые определяют общее решение системы.

Положим последовательно значения свободных переменных равными

и вычислим соответствующие значения базисных переменных. Полученные n-r решений линейно независимы и, следовательно, образуют фундаментальную систему решений исследуемой однородной системы:

В 41. Структура общего решения линейной однородной системы уравнений.

   Общее решение однородной линейной системы.

 

Рассмотрим однородную линейную систему

                         .                                      (4.2)

Отметим, что такая система всегда совместна, поскольку имеет нулевое решение   называемое тривиальным.

    Пусть ранг матрицы системы r<n. Предположим, что в базисный минор входят коэффициенты первых r уравнений. Тогда оставшиеся m – r уравнений  являются линейными комбинациями, то есть следствиями предыдущих. Поэтому можно оставить в системе только первые r уравнений:

. 

Оставим в левой части каждого уравнения неизвестные, коэффициенты при которых входят в базисный минор, а остальные неизвестные перенесем направо:

                               (4.3)

Эта система будет иметь единственное решение относительно неизвестных  выражающее их через остальные неизвестные ( ), которым можно придавать любые произвольные значения. Таким образом, система (4.2) при r<n является неопределенной.

 

Определение 4.7. Неизвестные  коэффициенты при которых входят в базисный минор матрицы системы, называются базисными неизвестными, а остальные ( ) –свободными неизвестными.

 

Определение 4.8. Решения системы (4.2)        (4.4) называются линейно независимыми, если линейная комбинация   дает нулевой столбец только при   

Покажем, что число линейно независимых решений системы (4.2) равно n – r. Действительно, рассмотрим столбцы вида

                                                     (4.5)              содержащие по  n-r  чисел. Очевидно, что эти столбцы линейно независимы, а любой другой столбец той же размерности является их линейной комбинацией. Пусть эти столбцы задают значения свободных неизвестных системы (4.2).

Тогда базисные неизвестные будут однозначно определяться для выбранных свободных неизвестных из системы (4.3) по правилу Крамера, и все решения системы, соответствующие наборам свободных неизвестных (4.5), образуют  n-r линейно независимых столбцов вида (4.4), то есть n-r линейно независимых решений системы (4.2).

 

Определение 4.9. Любые  n – r  линейно независимых решений системы (4.2) называются ее фундаментальной системой решений.

 

Определение 4.10. Фундаментальная система решений линейной однородной системы, в которой свободные неизвестные задаются по формулам (4.5), называется нормальной фундаментальной системой решений.

 

Замечание. Очевидным образом доказываются свойства решений однородной линейной системы (4.2):

Свойство 1. Сумма решений системы (4.2) является ее решением.

Свойство 2. Столбец решений (4.2), умноженный на любое число, тоже есть решение этой системы.

 

Следовательно, любая линейная комбинация фундаментальной системы решений системы (4.2) является ее решением. Можно доказать и обратное утверждение:

 

Теорема 4.3(без доказательства). Любое решение однородной линейной системы (4.2) является линейной комбинацией фундаментальной системы ее решений.

 

Таким образом, любое решение системы (4.2) имеет вид:

           , где  - фундаментальная система решений.

В 42. Неоднородная СЛАУ. Теорема Кронекера-Капелли.

Рассмотрим неоднородную систему m линейных алгебраических уравнений относительно nнеизвестных  x₁ , x₂ , ..., x_n:

В отличие от однородной системы, эта система совместна не всегда. Справедливо следующее утверждение (теорема Кронекера-Капелли).

Для того, чтобы неоднородная система линейных алгебраических уравнений была совместна, необходимо и достаточно, чтобы ранг расширенной матрицы системы совпадал с рангом матрицы системы.

Теорема: Система совместна (имеет хотя бы одно решение) тогда и только тогда, когда ранг матрицы системы равен рангу расширенной матрицы.

r(A) = r(A^*).

 

            Очевидно, что система (1) может быть записана в виде:

x₁  + x₂ + … + x_n

 

            Доказательство.

            1) Если решение существует, то столбец свободных членов есть линейная комбинация столбцов матрицы А, а значит добавление этого столбца в матрицу, т.е. переход А®А^* не изменяют ранга.

            2) Если r(A) = r(A^*), то это означает, что они имеют один и тот же базисный минор. Столбец свободных членов – линейная комбинация столбцов базисного минора, те верна запись, приведенная выше.

В 43. Структура общего решения неоднородной СЛАУ

Рассмотрим неоднородную линейную систему (2.2):

               .

Докажем следующие свойства ее решений:

Свойство 1. Сумма любого решения системы (2.2) и любого решения соответствующей однородной системы (4.2) является решением системы (2.2).

 

Доказательство.

Пусть с₁, с₂,…,с_n – решение системы (2.2), а d₁, d₂,…,d_n – решение системы (4.2) с теми же коэффициентами при неизвестных. Подставим в систему (2.2) x_i=c_i+d_i:

              .

После перегруппировки слагаемых получим:

            .

Но  Следовательно, x_i=c_i+d_i является решением системы (2.2).

 

Свойство 2. Разность любых двух решений неоднородной системы (2.2) является решением соответствующей однородной системы (4.2).

 

Доказательство.

Пусть   и  - решения системы (2.2). Тогда

Утверждение доказано.

 

Следствие. Общее решение неоднородной системы (2.2) представляет собой сумму общего решения соответствующей однородной системы (4.2) и частного решения системы (2.2).

 

Пример.

Общее решение системы   можно записать в виде:

, где  - частное решение данной системы.

 

В 44. Правило Крамера

Рассмотрим систему m линейных уравнений с n неизвестными

i=1,…..,m; j=1,…..,n,        

Коэффициенты и свободные члены СЛАУ запишем в виде матриц и назовем их: A - матрица системы, а A₁ - расширенная матрица системы.

,

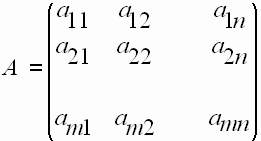(8.1)

Число уравнений СЛАУ равно числу неизвестных: m=n.

Теорема (правило Крамера): Система из n линейных алгебраических уравнений с n неизвестными в случае, когда определитель матрицы системы отличен от нуля

совместна и имеет единственное решение: для всех j: j = 1, 2, 3,…,n.

Здесь через D_j обозначен определитель матрицы, получаемой из матрицы c заменой j-го столбца (т.е. столбца коэффициентов при определяемом неизвестном) столбцом свободных членов, т.е.

В 45. Линейный оператор, его матрица в заданном базисе. Изменение координат вектора и матрицы линейного оператора при переходе к новому базису.

Пусть

, A — линейный оператор в Rⁿ.

Это означает, что в некотором базисе  в Rⁿ имют место разложения:

.

Поскольку A — линейный оператор, то

Но  следовательно,  т.е.  — вектор из Rⁿ, компоненты которого — координаты образа базисного вектора 

Продолжим вычисления:

Обозначим

.

Тогда    т.е.  .

Формула  связывает вектор-столбец  координат образа с вектором-столбцом  координат прообраза.

Определение. Матрица, столбцами которой являются координаты образов соответствующих базисных векторов некоторого базиса в Rⁿ —

• называется матрицей линейного оператора A в данном базисе.

Обратите внимание, теперь и в дальнейшем A (полужирная) — обозначение линейного оператора, A(светлая) или A_e —обозначение матрицы оператора A в некотором базисе или в базисе  .

Таким образом, доказана следующая теорема.

Теорема (связь координат образа и прообраза). Если в пространстве Rⁿ определен некоторый базис,  и  — векторы (столбцы) из Rⁿ и  , то векторы-столбцы их координат в этом базисе связаны соотношением  , где A — матрица оператора A в этом же базисе.

Между множеством линейных операторов, действующих в Rⁿ и множеством квадратных матриц порядка n можно установить взаимно однозначное соответствие.

Матрица нулевого оператора: поскольку  то   и, следовательно матрица нулевого оператора — нулевая матрица;

матрица тождественного (единичного) оператора:поскольку  , то  (единица на i-м месте), и, следовательно матрица тождественного оператора — единичная матрица;

матрица оператора проектирования пространства Rⁿ на подпространство R^n-1 параллельно вектору  : поскольку  , то   и, следовательно у матрицы A оператора проектирования последний столбец нулевой и она имеет вид:

матрица оператора поворота пространства R³ против часовой стрелки на угол ? относительно оси вектора  : поскольку  , то   и, следовательно у матрицы A оператора пооворота имеет вид:

Преобразование матрицы линейного оператора при изменении базиса

Как уже отмечалось, в пространстве Rⁿ существует множество различных базисов.

Пусть  и  — два базиса в Rⁿ.

Обозначим   и  координаты векторов  и  из Rⁿ и матрицу оператора A соответственно в базисах  и  , а  — матрица перехода от базиса   к базису  , т.е.

,

,

Тогда

откуда имеем

— формулы преобразования матрицы линейного оператора при изменении базиса.

В. 46 собственные значения и собственные векторы линейного оператора

Пусть задана квадратная матрица  , X – некоторая матрица–столбец, высота которой совпадает с порядком матрицы A.  .

Во многих задачах приходится рассматривать уравнение относительно X

,

где λ – некоторое число. Понятно, что при любом λ это уравнение имеет нулевое решение  .

Число λ, при котором это уравнение имеет ненулевые решения, называется собственным значением матрицы A, а X при таком λ называется собственным вектором матрицы A.

Найдём собственный вектор матрицы A. Поскольку E∙X = X, то матричное уравнение можно переписать в виде   или  . В развёрнутом виде это уравнение можно переписать в виде системы линейных уравнений. Действительно  .

И, следовательно, 

Итак, получили систему однородных линейных уравнений для определения координат x₁, x₂, x₃ вектора X. Чтобы система имела ненулевые решения необходимо и достаточно, чтобы определитель системы был равен нулю, т.е.

Это уравнение 3-ей степени относительно λ. Оно называется характеристическим уравнением матрицы A и служит для определения собственных значений λ.

Каждому собственному значению λ соответствует собственный вектор X, координаты которого определяются из системы при соответствующем значении λ.

В 47. Кривые второго порядка

                                Эллипс.        

 

Определение 11.2. Эллипсом  называется множество точек плоскости, для которых сумма расстояний до двух фиксированных точек F₁ и F₂ этой плоскости, называемых фокусами, есть величина постоянная.

 

Замечание. При совпадении точек F₁ и F₂ эллипс превращается в окружность.

    Выведем уравнение эллипса, выбрав декартову систему координат так, чтобы ось Ох совпала с прямой F₁F₂, начало     

    координат – с серединой отрезка F₁F₂. Пусть длина этого   отрезка равна 2с, тогда в выбранной системе координат

    F₁(-c, 0), F₂(c, 0). Пусть точка М(х, у) лежит на эллипсе, и сумма расстояний от нее до F₁ и F₂ равна 2а.

                                       Тогда r₁ + r₂ = 2a, но   ,

поэтому   Введя обозначение b² = a²-c² и проведя несложные алгебраические преобразования, получим каноническое уравнение эллипса:                                                                               

 

Определение 11.3. Эксцентриситетом эллипса называется величина е=с/а    (11.2)

 

Определение 11.4. Директрисой D_i эллипса, отвечающей фокусу F_i, называется прямая, расположенная в одной полуплоскости с F_i относительно оси Оу перпендикулярно оси Ох на расстоянии а/е от начала координат.

 

Замечание. При ином выборе системы координат эллипс может задаваться не каноническим уравнением (11.1), а уравнением второй степени другого вида.

 

                         Свойства эллипса:

1)       Эллипс имеет две взаимно перпендикулярные оси симметрии (главные оси эллипса) и центр симметрии (центр эллипса). Если эллипс задан каноническим уравнением, то его главными осями являются оси координат, а центром – начало координат. Поскольку длины отрезков, образованных пересечением эллипса с главными осями, равны 2а и 2b(2a>2b), то главная ось, проходящая через фокусы, называется большой осью эллипса, а вторая главная ось – малой осью.

2)       Весь эллипс содержится внутри прямоугольника 

3)       Эксцентриситет эллипса e < 1.                                                           

Действительно, 

4) Директрисы эллипса расположены вне эллипса (так как расстояние от центра эллипса до директрисы равно а/е, а е<1, следовательно, а/е>a, а весь эллипс лежит в прямоугольнике  )

5) Отношение расстояния r_i от точки эллипса до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету эллипса.

Доказательство.

Расстояния от точки М(х, у) до фокусов эллипса можно представить так:

 Составим уравнения директрис:

  (D₁),    (D₂). Тогда    Отсюда r_i / d_i = e, что и требовалось доказать.

Определение 11.5. Гиперболой  называется множество точек плоскости, для которых модуль разности расстояний до двух фиксированных точек F₁ и F₂ этой плоскости, называемыхфокусами, есть величина постоянная.

 

Выведем каноническое уравнение гиперболы по аналогии с выводом уравнения эллипса, пользуясь теми же обозначениями.

|r₁ - r₂| = 2a, откуда   Если обозначить b² = c² - a², отсюда можно получить

                    

                  - каноническое уравнение гиперболы.             (11.3)

 

 Определение 11.6. Эксцентриситетом гиперболы называется величина е = с / а.

 

Определение 11.7. Директрисой D_i гиперболы, отвечающей фокусу F_i, называется прямая, расположенная в одной полуплоскости с F_i относительно оси Оу перпендикулярно оси Ох на расстоянии а / е от начала координат.

 

                        Свойства гиперболы:

1)        Гипербола имеет две оси симметрии (главные оси гиперболы) и центр симметрии (центр гиперболы). При этом одна из этих осей пересекается с гиперболой в двух точках, называемых вершинами гиперболы. Она называется действительной осью гиперболы (ось Ох для канонического выбора координатной системы). Другая ось не имеет общих точек с гиперболой и называется ее мнимой осью (в канонических координатах – ось Оу). По обе стороны от нее расположены правая и левая ветви гиперболы. Фокусы гиперболы располагаются на ее действительной оси.

2)        Ветви гиперболы имеют две асимптоты, определяемые уравнениями

                                     и    .

3) Наряду с гиперболой (11.3) можно рассмотреть так называемую сопряженную гиперболу, определяемую каноническим уравнением

                    ,                                                                      (11.3`) 

для которой меняются местами действительная и мнимая ось с сохранением тех же асимптот.

4) Эксцентриситет гиперболы e > 1.

5)   Отношение расстояния r_i от точки гиперболы до фокуса F_i к расстоянию d_i от этой точки до отвечающей фокусу директрисы равно эксцентриситету гиперболы.

Доказательство можно провести так же, как и для эллипса.

Определение 11.8. Параболой называется множество точек плоскости, для которых расстояние до некоторой фиксированной точки F этой плоскости равно расстоянию до некоторой фиксированной прямой. Точка F называется фокусом параболы, а прямая – ее директрисой.

Для вывода уравнения параболы выберем декартову систему координат так, чтобы ее началом была середина перпендикуляра FD, опущенного из фокуса на директрису, а координатные оси располагались параллельно и перпендикулярно директрисе. Пусть длина отрезка FD равна р. Тогда из равенства r = d следует, что

                                                          поскольку

 

Алгебраическими преобразованиями это уравнение можно привести к виду:    y² = 2px , называемому каноническим уравнением параболы. Величина р называется параметром параболы.

 

                       Свойства параболы:

1)       Парабола имеет ось симметрии (ось параболы). Точка пересечения параболы с осью называется вершиной параболы. Если парабола задана каноническим уравнением, то ее осью является ось Ох, а вершиной – начало координат.

2)       Вся парабола расположена в правой полуплоскости плоскости Оху.

 

Замечание. Используя свойства директрис эллипса и гиперболы и определение параболы, можно доказать следующее утверждение:

Множество точек плоскости, для которых отношение е расстояния до некоторой фиксированной точки к расстоянию до некоторой прямой есть величина постоянная, представляет собой эллипс (при e<1), гиперболу (при e>1) или параболу (при е=1).

 

В. 48 Поверхности второго порядка

Поверхности второго порядка – это поверхности, которые в прямоугольной системе координат определяются алгебраическими уравнениями второй степени.    Эллипсоид        Эллипсоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением :                                                         (1)     Уравнение (1) называется каноническим уравнением эллипсоида.     Установим геометрический вид эллипсоида. Для этого рассмотрим сечения данного эллипсоида плоскостями, параллельными плоскости Oxy. Каждая из таких плоскостей определяется уравнением вида z=h, где h – любое число, а линия, которая получается в сечении, определяется двумя уравнениями                                                 (2) Исследуем уравнения (2) при различных значениях h. 1)     Если  > c (c>0), то    и уравнения (2) определяют мнимый эллипс, т. е. точек пересечения плоскости z=h с данным эллипсоидом не существует. 2)     Если  , то   и линия (2) вырождается в точки (0; 0; + c) и (0; 0; - c)(плоскости   касаются эллипсоида). 3)     Если  , то уравнения (2) можно представить в виде откуда следует, что плоскость z=h пересекает эллипсоид по эллипсу с полуосями   и  . При уменьшении   значения  и  увеличиваются и достигают своих наибольших значений при  , т. е. в с ечении эллипсоида координатной плоскостью Oxy получается  самый большой эллипс с полуосями   и  . Аналогичная картина получается и при пересечении данной поверхности плоскостями, параллельными координатным плоскостям Oxz и Oyz. Таким образом, рассмотренные сечения позволяют изобразить эллипсоид как замкнутую овальную поверхность (рис. 156). Величины a, b, c называются полуосямиэллипсоида. В случае a=b=c эллипсоид является сферой Однополосный гиперболоид       Однополосным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением             (3)     Уравнение (3) называется каноническим уравнением однополосного гиперболоида.    Установим вид поверхности (3). Для этого рассмотрим сечение ее координатными плоскостями Oxy (y=0) и Oyx (x=0). Получаем соответственно уравнения                                      и         из которых следует, что в сечениях получаются гиперболы.    Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy . Линия, получающаяся в сечении, определяется уравнениями                            или          (4) из которых следует, что плоскость z=h пересекает гиперболоид по эллипсу с полуосями      и   , достигающими своих наименьших значений при h=0, т.е. в сечении данного гиперболоида координатной осью Oxy получается самый маленький эллипс с полуосями a*=a и b*=b. При бесконечном возрастании   величины a* и b* возрастают бесконечно. Таким образом, рассмотренные сечения позволяют изобразить однополосный гиперболоид в виде бесконечной трубки, бесконечно расширяющейся по мере удаления (по обе стороны) от плоскости Oxy. Величины a, b, c называются полуосями однополосного гиперболоида. Двуполостный гиперболоид.      Двуполостным гиперболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением                             (5)     Уравнение (5) называется каноническим уравнением двуполостного гиперболоида.    Установим геометрический вид поверхности (5). Для этого рассмотрим его сечения координатными плоскостями Oxy и Oyz. Получаем соответственно уравнения                                 и    из которых следует, что в сечениях получаются гиперболы.      Теперь рассмотрим сечения данного гиперболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, полученная в сечении, определяется уравнениями                                   или             (6)  из которых следует, что при   >c (c>0) плоскость z=h пересекает гиперболоид по эллипсу с полуосями     и   . При увеличении   величины a* и b*тоже увеличиваются При      уравнениям (6) удовлетворяют координаты только двух точек: (0;0;+с) и (0;0;-с)  (плоскости    касаются данной поверхности). При    уравнения (6) определяют мнимый эллипс, т.е. точек пересечения плоскостиz=h с данным гиперболоидом не существует. Величина a, b и c называются полуосями двуполостного гиперболоида.  Эллиптический параболоид.     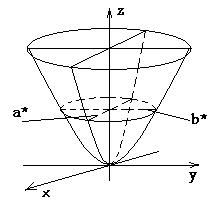Эллиптическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением   (7) где p>0 и q>0.    Уравнение (7) называется каноническим уравнением эллиптического параболоида.    Рассмотрим сечения данной поверхности координатными плоскостями  Oxy и Oyz. Получаем соответственно уравнения                                              и   из которых следует, что в сечениях получаются параболы, симметричные относительно оси Oz, с вершинами в начале координат. Теперь рассмотрим сечения данного параболоида плоскостями z=h, параллельными координатной плоскости Oxy. Линия, получающаяся в сечении, определяется уравнениями                                      или            (8) из которых следует, что при   плоскость z=h пересекает эллиптический параболоид по эллипсу с полуосями    и  . При увеличении h величины a и b тоже увеличиваются; при h=0 эллипс вырождается в точку (плоскость z=0 касается данного гиперболоида). При h<0 уравнения (8) определяют мнимый эллипс, т.е. точек пересечения плоскости z=h с данным гиперболоидом нет. Таким образом, рассмотренные сечения позволяют изобразить эллиптический параболоид в виде бесконечно выпуклой чаши. Точка (0;0;0) называется вершиной параболоида; числа p и q – его параметрами. В случае p=q уравнение (8) определяет окружность с центром на оси Oz, т.е. эллиптический параболоид можно рассматривать как поверхность, образованную вращением параболы вокруг её оси (параболоид вращения). Гиперболический параболоид Гиперболическим параболоидом называется поверхность, которая в некоторой прямоугольной системе координат, определяется уравнением        (9)                  где p>0, q>0.      Уравнение (9) называется каноническим уравнением гиперболического параболоида.      Рассмотрим сечение параболоида плоскостью Oxz (y=0). Получаем уравнение                                                 (10) из которых следует, что в сечении получается парабола, направленная вверх, симметричная относительно оси Oz, с вершиной в начале координат. В сечениях поверхности плоскостями, параллельными плоскости Oxz (y=h), получаются так же направленные вверх параболы.                                             рассмотрим сечение данного параболоида плоскостью Oyz (x=0). Получаем уравнение                                                  из которых следует, что и в этом случае в сечении получается парабола, но теперь направленная вниз, симметричная относительно оси Oz, с вершиной в начале координат. Рассмотрев сечения параболоида плоскостями, параллельными плоскости Oyz (x=h), получим уравнения                                           из которых следует, что при любом h в сечении получается парабола, направленная вниз, а вершина её лежит на параболе, определённой уравнениями (10). Рассмотрим сечения параболоида плоскостями z=h, параллельными плоскости Oxy . получим уравнения                            или   из которых следует, что при h>0 в сечении получаются гиперболы, пересекающие плоскость Oxy; при h<0 – гиперболы, пересекающие плоскости Oyz; при h=0 – гипербола вырождается в пару пересекающихся прямых                                 и   точка (0;0;0) называется вершиной параболоида; числа p и q – его  параметрами.   6.   Конус второго порядка .       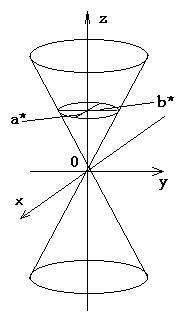Конусом второго порядка называется поверхность, которая в некоторой прямоугольной системе координат определяется уравнением                              (11)  Рассмотрим геометрические свойства конуса. В сечение этой поверхности плоскостью Oxy (y=0) получаем линию                                    распадающуюся на две пересекающиеся прямые                              и   Аналогично, в сечении конуса плоскостью Oyz (x=0) также  получаются две пересекающиеся прямые                                                      и   Рассмотрим сечения поверхности плоскостями z=h, параллельными плоскости Oxy. Получим                                               или   из которых следует, что при h>0 и h<0 в сечениях получаются эллипсы с полуосями     . При  увеличении абсолютной величины h полуоси a* и b* также увеличиваются. При h=0 линия пересечения поверхности с плоскостью z=h вырождается в точку (0;0;0).