2. Теорема Лагранжа

Результаты теоремы Ролля используются при рассмотрении следующей теоремы о среднем, принадлежащей Лагранжу (1736–1813).

Теорема. Если функция непрерывна на отрезке и дифференцируема во всех его внутренних точках, то существует, по крайней мере, одна точка , в которой .

Доказательство. Рассмотрим график функции (рис. 2.1).

Проведем хорду, соединяющую точки и , и запишем ее уравнение. Воспользовавшись уравнением прямой, проходящей через две точки на плоскости, получим:

,

откуда:

Рис. 2.1

и .

Составим теперь вспомогательную функцию, вычтя из уравнения кривой уравнение хорды:

.

Полученная функция непрерывна на отрезке и дифференцируема во всех его внутренних точках. Кроме того, вычисление в точках и показывает, что . Значит, функция на отрезке удовлетворяет требованиям теоремы Ролля. Но в этом случае существует такая точка , в которой .

Вычислим производную функции :

.Согласно теореме Ролля в точке производная , то есть и ,

что и требовалось доказать.

Геометрический смысл теоремы Лагранжа следующий: внутри отрезка существует, по крайней мере, одна точка, в которой касательная параллельна хорде, стягивающей кривую на данном отрезке. В частности, при теорема переходит в теорему Ролля.

Теорему Лагранжа часто записывают в следующем виде:

,

то есть приращение функции равно приращению аргумента, умноженному на производную функции в некоторой внутренней точке. В связи с этим теорему Лагранжа называют также теоремой о конечных приращениях.

3. Теорема Коши

Рассмотрим, наконец, третью теорему о среднем, принадлежащей Коши (1789–1859), которая является обобщением теоремы Лагранжа.

Теорема. Если функции и непрерывны на отрезке и дифференцируемы во всех его внутренних точках, причем не обращается в ноль ни в одной из указанных точек, то существует, по крайней мере, одна точка , в которой .

В. 34 Матрицы. Действия над матрицами. Определители 2, 3-го и более высокого порядка. Свойства определителей. Обратная матрица.

Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество п столбцов. Числа т и п называются порядками матрицы. В случае, если т = п, матрица называется квадратной, а число m = n — ее порядком.

Для краткого обозначения матрицы часто будет использоваться либо одна большая латинская буква (например, A), либо символ || a _ij || , а иногда с разъяснением: А = || a _ij || = ( a _ij ), где (i = 1, 2, ..., т, j=1, 2, ..., n).

Числа a _ij , входящие в состав данной матрицы, называются ее элементами. В записи a _ij первый индекс і означает номер строки, а второй индекс j — номер столбца. В случае квадратной матрицы

(1.1)

вводятся понятия главной и побочной диагоналей. Главной диагональю матрицы (1.1) называется диагональ а₁₁ а₁₂ … a_nn идущая из левого верхнего угла этой матрицы в правый нижний ее угол. Побочной диагональю той же матрицы называ­ется диагональ а_n1 а_(n-1)2 … a_1n , идущая из левого нижнего угла в правый верхний угол.

Две матрицы   и   одинакового размера m на n называются равными, если   , i = 1,2,…,m, j=1,2,…,n.

Если матрицы A и B равны, то будем писать A=B.

Линейные операции. Суммой двух матриц A и B размера m на n называется матрица C размера m на n, элементы которой определяются равенством

Сумму матриц A и B будем обозначать C=A+B.

Матрица   называется противоположной к матрице   .

Теорема 2.1 Операция сложения матриц обладает следующими свойствами: для любых матриц   и нулевой матрицы 

1) A+B=B+A; (перестановочность или коммутативность операции сложения

2) (A+B)+C = A+(B+C); (ассоциативность или сочетательное свойство)

3) A+O = O+A =A;

4) A+(-A)=(-A)+A=O.

Перечисленные выше свойства непосредственно вытекают из определения и доказываются по единой схеме.

Разностью матриц   и   называется матрица A+(-B).

Разность матриц A и B будем обозначать A-B.

Произведением матрицы   на число   называется матрица  , элементы которой определены равенством

Произведение матрицы A на число   будем обозначать   .

Теорема 2.2 Операция умножения матрицы на число обладает следующими свойствами:

1)   ;

2)   ;

3)   (Распределительное свойство относительно сложения матриц);

4)   (Распределительное свойство относительно сложения чисел);

5) -A=(-1)A.

Все перечисленные свойства непосредственно вытекают из определения.

Операции сложения матриц и умножения матрицы на число позволяют для произвольных матриц   одинакового размера   и произвольных чисел  однозначно определить матрицу   , называемуюлинейной комбинацией матриц   с коэффициентами   .

Умножение матриц. Произведением матриц   и  называется матрица   , элементы которой определены равенством

Произведение матриц A и B будем обозначать C=AB.

Из определения следует, что произведение AB определено лишь в том случае, когда число столбцов матрицы A совпадает с числом строк матрицы B. Это означает, что оба произведения AB и BA определены тогда и только тогда, когда матрицы A и B имеют размеры   и   соответственно. Следовательно равенство AB=BA возможно лишь для квадратных матриц одинакового порядка. Однако и в этом случае произведение матриц, вообще говоря, зависит от порядка сомножителей.

Матрицы A и B называются перестановочными или коммутирующими, если AB=BA.

Теорема 2.3 Операция умножения матриц обладает следующими свойствами:

1) (AB)C=A(BC); (Свойство ассоциативности)

2)   , для любого действительного числа 

3) A(B+C)=AB+AC, (A+B)C=AC+BC (Свойство дистрибутивности), для любых матриц A, B, C,для которых левые части равенств имеют смысл.

Справедливость свойств 2) и 3) доказываются непосредственно.

В качестве иллюстрации приведём доказательство первого равенства свойства 3). Пусть  ,   ,   . Матрицы A(B+C) и AB+ACимеют одинаковый размер -   . Пусть   - элемент матрицы A(B+C) в позиции (i,j),  - элемент матрицы AB+AC в позиции (i,j), тогда

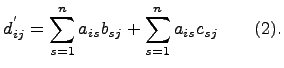
Из равенств (1) и (2) следует, что   , что доказывает первое равенство свойства 3).

Определение: Транспонированием матрицы называется замена строк матрицы на её столбцы с сохранением их номеров. Полученная матрица обозначается А^T. Т.е., если исходная матрица имеет вид

то

Транспонированная матрица обладает следующими свойствами:

• дважды транспонированная матрица равна исходной матрице, т.е. (А^T)^T=A;

• при транспонировании квадратных матриц элементы, находящиеся на главной диагонали, не меняют своих позиций;

• симметрическая матрица не изменяется при транспонировании.

Определители второго и третьего ранга.

В приложениях часто встречаются определители второго и третьего порядков. Рассмотрим основные правила их вычисления.

Определитель второго порядка вычисляется по следующему правилу:

или схематично

(4.1)

Соответствующее правило вычисления для определителя третьего порядка имеет вид:

(4.2)

При его вычислении часто удобно пользоваться мнемоническим правилом Саррюса:

(4.3)

приписать к определителю справа два первых столбца, не меняя их порядка, и составить сумму произведений элементов главной диагонали и элементов, параллельных ей, из которой затем вычесть сумму произведений элементов побочной диагонали и элементов параллельных ей.

В общем случае для вычисления определителя n - го порядка справедлива.

Теорема о разложении: Определитель равен сумме парных произведений элементов какого-либо ряда (строки или столбца) его на их алгебраические дополнения.

Таким образом, для определителя (3.1) справедливы следующие разложения:

разложение по i-ой строке

(4.4)

разложение по j -ому столбцу

Миноры матрицы

Пусть дана квадратная матрица А, n - ого порядка. Минором некоторого элемента а_ij , определителя матрицы n - ого порядка называется определитель (n - 1) - ого порядка, полученный из исходного путем вычеркивания строки и столбца, на пересечении которых находится выбранный элемент а_ij. Обозначается М_ij.

Рассмотрим на примере определителя матрицы 3 - его порядка:

тогда согласно определению минора, минором М₁₂, соответствующим элементу а₁₂, будет определитель:

При этом, с помощью миноров можно облегчать задачу вычисления определителя матрицы. Надо разложить определитель матрицы по некоторой строке и тогда определитель будет равен сумме всех элементов этой строки на их миноры. Разложение определителя матрицы 3 - его порядка будет выглядеть так:

знак перед произведением равен (-1)ⁿ, где n = i + j.

Алгебраические дополнения:

Алгебраическим дополнением элемента а_ij называется его минор, взятый со знаком "+", если сумма (i + j) четное число, и со знаком "-", если эта сумма нечетное число. Обозначается А_ij.

А_ij = (-1)^i+j × М_ij.

Тогда можно переформулировать изложенное выше свойство. Определитель матрицы равен сумме произведений элементов некторого ряда (строки или столбца) матрицы на соответствующие им алгебраические дополнения.

Свойство № 1: Определитель матрицы не изменится, если его строки заменить столбцами, причем каждую строку столбцом с тем же номером, и наоборот (Транспонирование). |А| = |А|^Т

Следствие:

Столбцы и строки определителя матрицы равноправны, следовательно, свойства присущие строкам выполняются и для столбцов.

Свойство № 2: При перестановке 2-х строк или столбцов определитель матрицы изменит знак на противоположный, сохраняя абсолютную величину, т.е.:

Свойство № 3: Определитель матрицы, имеющий два одинаковых ряда, равен нулю.

Свойство № 4: Общий множитель элементов какого-либо ряда определителя матрицы можно вынести за знак определителя.

Следствия из свойств № 3 и № 4: Если все элементы некоторого ряда (строки или столбца) пропорциональны соответствующим элементам параллельного ряда, то такой определитель матрицы равен нулю.

Свойство № 5: Если все элементы какой–либо строки или столбца определителя матрицы равны нулю, то сам определитель матрицы равен нулю.

Свойство № 6: Если все элементы какой–либо строки или столбца определителя представлены в виде суммы 2-х слагаемых, то определитель матрицы можно представить в виде суммы 2-х определителей по формуле:

Свойство № 7: Если к какой–либо строке (или столбцу) определителя прибавить соответствующие элементы другой строки (или столбца), умноженные на одно и тоже число, то определитель матрицы не изменит своей величины.

Теорема. Всякая невырожденная (т.е. определитель которой отличен от нуля) квадратная матрица A имеет обратную матрицу A^-1, которая находится по формуле:

при этом A٠A^-1=A^-1٠A=E.

Правило (алгоритм) нахождения обратной матрицы

Пусть дана квадратная матрица .

Шаг 1-ый. Вычислим det(A) и убедимся при этом, что det(A)≠0 , то есть матрица A - невырожденная.

Шаг 2-ой. Подсчитаем алгебраические дополнения A_ij для всех элементов a_ij матрицы A и составляем матрицу

.

Шаг 3-ий. Транспонируем матрицу и образуем присоединенную матрицу

Шаг 4-ый. Составляем обратную матрицу по следующему правилу:

(5.2)

Алгоритм вычисления обратной матрицы.

1. Находим определитель матрицы, т.е. .

2. Находим транспонированную матрицу, т.е. .

3. Находим присоединенную матрицу, т.е (матрица, состоящая из алгебраических дополнений к элементам транспонированной матрицы).

4. Вычисляем обратную матрицу по формуле .

5. Проверяем правильность вычисления, исходя из определения обратной матрицы.

В 35. Геометрические векторы, линейные оперции с ними.

Вектором, или геометрическим вектором,  называется направленный отрезок. (Перемещение, сила, скорость)

Длина вектора AB называется расстояние между точками А и В, и обозначается символом |a¯|=|AB¯¯|. Вектор нулевой длины называется нулевым вектором и обозначается символом 0¯.

Векторы, расположенные на параллельных прямых или на одной прямой называются коллинеарными. Если два коллинеарных вектора имеют одинаковое направление, то они называются сонаправленными, в противном случае – противоположно направленными.

Два вектора считаются равными, если они сонаправлены и равны по модулю.

Вектор называется единичным, если его длина равна 1.

Ортом вектора а называется вектор единичной длины, сонаправленный с вектором а.

Суммой   двух векторов   и   называется вектор, который идет из начала вектора   в конец вектора   при условии, что вектор   приложен к концу вектора   (правильно треугольника). Построение суммы   изображено на рис. 1.

Наряду с правилом треугольника часто пользуются (равносильным ему) правилом параллелограма: если векторы   и  приведены к общему началу и на них построен параллелограмм, то сумма   есть вектор, совпадающий с диагональю этого паралеллограмма, идущей из общего начала   и   (рис. 2). Отсюда сразу следует, что  .

Разность   двух векторов   и   называется вектор, который в сумме с вектором   составляет вектор  . Если два вектора   и   приведены к общему началу, то разность их   есть вектор, идущий из конца   («вычитаемого») к концу  («уменьшаемого»).

Два вектора равной длины, лежащие на одной прямой и направленные в противоположные стороны, называются противоположными: если один из них обозначен символом  , то другой обозначается символом  .

Легко видеть, что  .

Таким образом, построение разности равносильно прибавлению к «уменьшаемому» вектора, обратного «вычитаемого».

Произведением вектора a¯ на действительное число λ называется вектор, обозначаемый λa¯¯ такой, что:

1) |λa¯|=|λ|⋅|a¯|;

 

2) векторы a¯ и λa¯ сонаправлены при λ>0 и противоположно направлены при λ<0.

 Свойства сложения, произведения вектора на число.

1^о.   +   =   +   (переместительный закон).

2^о.   + (  +  ) = (  +  ) +   = (  +  ) +   (сочетательный закон).

3^о.   + (– ) +  .

4^о. (k + l)  = k  + l .

 k(  +  ) = k  + k .

5^o. k(l ) = (kl) .

6^o. 1×  =  , (–1) ×  = –  , 0 ×  =  .

Говорят, что вектор а является линейной комбинацией векторов a₁, a₂, a₃, ..., a_n, если он представим в виде

а = x₁a₁+ x₂a₂+ x₃a₃+ ...+ x_na_n,

где x₁ , x₂ ,..., x_n — некоторые числа.

Так, вектор а = 3a₁ — 5a₂ + ¹/₂ a₃ есть линейная комбинация векторов a₁, a₂ и a₃.

В системе координат Оxyz числа x, y, z называются координатами точки М , соответственно абсциссой, ординатой и аппликатой, и записываются в виде упорядоченной точки чисел: M (x; y; z) (рис.3). В ектор единичной длины, направление которого совпадает с направлением оси, называют единичным вектором(или ортом) оси. Обозначим через

Соответственно орты координатных осей Ox, Oy, Oz

Теорема. Всякий вектор может быть разложен по ортам координатных осей.

Доказательство. Пусть  - произвольный вектор пространства  , а x, y, z – его проекции на координатные оси. Так как мы рассматриваем свободные векторы, то совместим начало вектора  с началом координат и получим вектор  с теми же координатами x, y, z (рис.4).

С огласно правилу сложения векторов, имеем

Но

значит,

На основании правила умножения вектора на скаляр можно выразить составляющие вектора  через его проекции и орты осей:

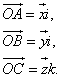Тогда предыдущее векторное равенство примет вид

        (2)

Докажем единственность такого представления. Пусть a = x₁i  + у₁j +z₁k  и   a = x₂i  + у₂j+z₂k. из первого равенства вычтем второе 0= (x₁-x₂)i +(y₁-y₂)j + (z₁-z₂)k

Но так как векторы i, J, k неколлинеарны, то равенство возможно только при x₁ = x₂ и у₁ = у₂ z₁=z₂. Единственность доказана.

Равенство (2) называется разложением вектора по координатным осям. Коэффициентами этого разложения являются проекции вектора на координатные оси. Таким образом, коэффициентами разложения (2) вектора по координатным осям являются координаты вектора.

Пусть в заданной системе координат начало вектора  находится в точке

а конец – в точке

(рис.5).

Т огда

Из равенства

следует, что

Отсюда

или в координатной форме

         

Следовательно, координаты вектора равны разностям одноимённых координат конца и начала вектора. 

Условие коллинеарности векторов

необходимому и достаточному условию коллинеарности двух ненулевых векторов: для коллинеарности двух векторов   и   необходимо и достаточно, чтобы они были связаны равенствами   , т.е. координаты векторов пропориональны.

В 36. Векторное, смешанное и скалярное произведения векторов.

Определение: Под скалярным произведением двух векторов   и 

понимается число, равное произведению длин этих векторов на косинус угла между ними, т.е.  = ,    - угол между векторами   и  . 

 Свойства скалярного произведения:

1.    a b =  

2.     (  +   )  =

3.     

4.     

5.      , где    – скаляры.

6.     два вектора перпендикулярны (ортогональны), если   .

7.      тогда и только тогда, когда  .

Теорема: Скалярное произведение в координатной форме имеет вид:  , где   и  .

Доказательство

Чтобы выразить скалярное произведение

в координатной форме, предварительно найдём скалярные произведение ортов (cвойство 3).

Так как векторы

попарно перпендикулярны, то

Теперь выполним умножение векторных многочленов:

 

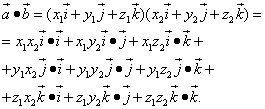
Подставляя в правую часть равенства значения соответствующих скалярных произведений ортов, получим

              

Пример: Найти скалярное произведение векторов   и 

Решение: 

Определение: Под векторным произведением двух векторов   и   понимается вектор,   для которого:

1) , где  угол между векторами   и 

2) 

3) вектор с направлен так, что от его конца, кратчайший поворот от а к b виден против часовой стрелки, то есть они (a,b,c) образуют правую тройку векторов.

Геометрический смысл векторного произведения

модуль вектора c =[ab]равен площади параллелограмма, построенного на данных векторах a и b, т.е. 

 Свойства векторного произведения:

1.При изменении порядка сомножителей векторное произведение меняет свой знак на обратный, сохраняя модуль, т.е. 

2.Векторный квадрат равен нуль-вектору, т.е. 

3.Скалярный множитель можно выносить за знак векторного произведения, т.е. 

4.Для любых трех векторов    справедливо равенство 

5.Необходимое и достаточное условие коллинеарности двух векторов   и  : 

 Векторное произведение в координатной форме.

 Если известны координаты векторов   и  , то их векторное произведение находится по формуле:

   .

Векторы a,b, c называются компланарными, если они лежат в одной плоскости или параллельных плоскостях.

Определение: Смешанным (векторно-скалярным) произведением векторов   называется число, определяемое по формуле:  .

 Свойства смешанного произведения:

1.Смешанное произведение не меняется при циклической  перестановке его сомножителей, т.е.  .

2.При перестановке двух соседних сомножителей смешанное произведение меняет свой знак на противоположный, т.е.  .

3.Необходимое и достаточное условие компланарности трех векторов  :  =0.

4.Смешанное произведение трех векторов равно объему параллелепипеда, построенного на этих векторах, взятому со знаком плюс, если эти векторы образуют правую тройку, и со знаком минус, если они образуют левую тройку, т.е.  .

 Если известны координаты векторов  , то смешанное произведение находится по формуле: 

В 37. Плоскость и прямая в пространстве 

                          Плоскость в пространстве. 

   Получим сначала уравнение плоскости, проходящей через точку М₀(х₀ ,у₀ ,z₀) перпендикулярно вектору n = {A,B,C},называемому нормалью к плоскости. Для любой точки плоскости М(х, у,z) вектор М₀М = {x - x₀ , y - y_{0 ,} z - z₀) ортогонален вектору n, следовательно, их скалярное произведение равно нулю:

                    A(x - x₀) + B(y - y₀) + C(z - z₀) = 0.                                                 (8.1)

Получено уравнение, которому удовлетворяет любая точка заданной плоскости – уравнение плоскости, проходящей через данную точку перпендикулярно данному вектору.

    После приведения подобных можно записать уравнение (8.1) в виде:

                    Ax + By + Cz + D = 0,                                                                (8.2)

где D = -Ax₀ - By₀ - Cz₀. Это линейное уравнение относительно трех переменных называют общим уравнением плоскости.

 

                         Неполные уравнения плоскости.

   Если хотя бы одно из чисел А, В, С, D равно нулю, уравнение (8.2) называют неполным.

Рассмотрим возможные виды неполных уравнений:

1)       D = 0 – плоскость Ax + By + Cz = 0 проходит через начало координат.

2)       А = 0 – n = {0,B,C} Ox, следовательно, плоскость By + Cz + D = 0 параллельна оси Ох.

3)       В = 0 – плоскость Ax + Cz +D = 0 параллельна оси Оу.

4)       С = 0 – плоскость Ax + By + D = 0 параллельна оси Оz.

5)       А = В = 0 – плоскость Cz + D = 0 параллельна координатной плоскости Оху (так как она параллельна осям Ох и Оу).

6)       А = С = 0 – плоскость Ву + D = 0 параллельна координатной плоскости Охz.

7)       B = C = 0 – плоскость Ax + D = 0 параллельна координатной плоскости Оуz.

8)       А = D = 0 – плоскость By + Cz = 0 проходит через ось Ох.

9)       B = D = 0 – плоскость Ах + Сz = 0 проходит через ось Оу.

10)    C = D = 0 -  плоскость Ax + By = 0 проходит через ось Oz.

11)    A = B = D = 0 – уравнение Сz = 0 задает координатную плоскость Оху.

12)    A = C = D = 0 – получаем Ву = 0 – уравнение координатной плоскости Охz.

13)    B = C = D = 0 – плоскость Ах = 0 является координатной плоскостью Оуz.

Если же общее уравнение плоскости является полным ( то есть ни один из коэффициентов не равен нулю), его можно привести к виду:

                                                                                                          (8.3)

называемому уравнением плоскости в отрезках. Параметры а, b и с равны величинам отрезков, отсекаемых плоскостью на координатных осях.