4.3. Наборы растровых данных. Расширения растров.

Наборы растровых данных

Растровые данные представляют собой географические объекты путем деления территории на дискретные квадратные или прямоугольные ячейки, вложенные в сетку. Каждая ячейка имеет значение, которое используется для представления некоторых характеристик для этого места.

Растровые данные обычно используются для управления и представления изображений, цифровых моделей рельефа, а также ряда других явлений. Нередко растры используются как способ представления точечных, линейных и полигональных пространственных объектов.

Расширения растров

Растры интенсивно используются в Г ИС приложениях. База геоданных может управлять растрами для многих целей:

- в качестве индивидуальных наборов данных,

- в качестве логической коллекции наборов данных,

- атрибуты изображений в таблицах.

База геоданных содержит следующие элементы, которые образуют расширения растров:

1) Набор растровых данных – управляет очень большими непрерывными наборами данных изображений и мозаиками изображений.

2) Каталоги растров– используются для ряда целей: управлять слоем листов изображений, где каждый лист есть изображение; управлять серией изображений в СУ БД; управлять серией временных растров.

3) Колонки атрибутов растров в таблицах – хранит изображения или сканированные документы как атрибуты в таблице.

4) Определение сервиса изображения– сервисы публикации изображений для коллекции растровых данных в поле на диске, в ката логе изображений и базе геоданных.

13 Пространственный анализ векторных моделей

1.Алгоритмы вычислительной геометрии

1.1. Пересечение линий

Операция нахождения точки пересечения линий является одной из базовых в ГИС–анализе, так как она используется в ряде операций геопроцессинга и в оверлейных операциях.

Исходным является уравнение прямой, известное из аналитической геометрии:

y = kx + b ( 5.2.1) где:

b – отрезок, отсекаемый прямой на оси OY;

k – угловой коэффициент прямой k = tgb;

β – угол между положительным направлением оси OХ и прямой.

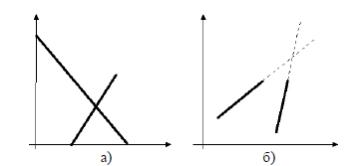
Рис. 5.2.1 – Точка пересечения: а) внутри отрезков прямых; б) снаружиотрезков прямых.

Две линии задаются уравнениями

Совместное решение этих двух уравнений позволяет найти координаты точки пересечения этих двух линий:

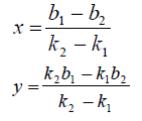
В оверлейных операциях при определении принадлежности точки полигону учитывается специальный случай, когда одна линия параллельна выбранной оси, например, оси ОХ. В этом случае k = 0, а координаты точки пересечения таких двух линий будут равны:

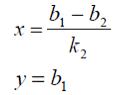
Для определения пересечения двух полилиний с n1 и n2 сегментами разработано несколько способов. Самым простым способом нахождения их точек пересечения

является последовательная проверка пересечения каждого сегмента первой линии с каждым сегментом второй линии. Сложность э того алгоритма пропорциональна произведению n1 * n2. Она может быть уменьшена, если предварительно проверять на пересечение экстенты (Extent – минимальный ограничивающий прямоугольник) сегментов и полилиний, представленные на рис.5.2.2.

Рис. 5.2.2 - Экстенты сегментов и полилинии

Второй метод, использованный в ГИС ArcInfo, основан на разбиении полилинии на секции, в которых линия монотонно возрастает или убывает по x и по y. Разбиение происходит в точках локального минимума или максимума по x или по y. Горизонтальная или вертикальная линия пересекает такую секцию только в одной точке.