Питання до мкр №2 з дисципліни «Основи теорії кіл, сигнали та процеси в електроніці »

1. Сигнали з обмеженим спектром. Ідеальний низькочастотний сигнал. Ортогональні сигнали з обмеженим спектром.

Любой ограниченный во времени сигнал обладает бесконечно широким спектром. Однако работа с бесконечно широким спектром в реальных условиях невозможна. Реальные РТ устройства обладают ограниченной полосой пропускания.

(сигнал с ограниченным спектром)

Ограниченному по частоте спектру соответствует временная функция в бесконечно широком интервале времени.

Рассмотрим конкретную задачу, когда в пределах частот среза спектральная плотность есть величина постоянная.

-верхняя частота.

Определим вид сигнала, имеющего ограниченный по оси частот спектр.

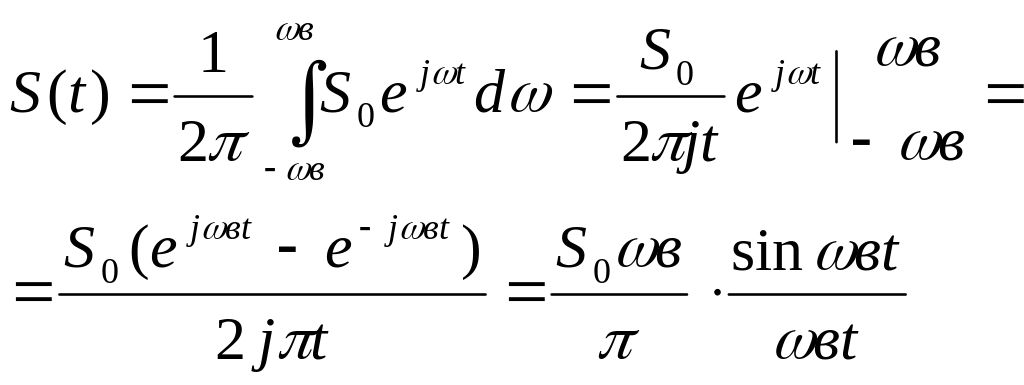
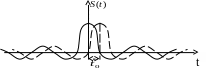
В результате вычислений получена функция в виде арочного синуса.

Согласно последнему выражению с ростом возрастает и значение самого сигнала и при достигает своего максимального значения. При очень узком спектре, когда , идеальный низкочастотный сигнал превратится в протяженную функцию. В свою очередь, когда ширина спектра сигнала очень велика и стремится , сигнал вырождается в δ – функцию.

Семейство сигналов этого типа можно обобщить, вводя временную задержку на оси времени.

Обозначим такой сигнал, как .

Тогда:

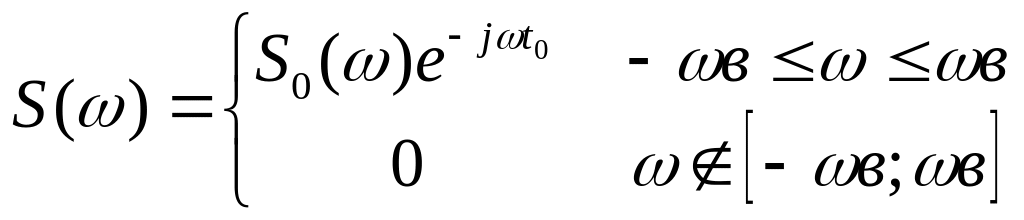
Свойства сигналов с ограниченным спектром позволяет найти новый интересный класс ортогональных сигналов. Данный класс идеально подходит для представления сигналов с ограниченным спектром.

Простейший пример таких сигналов это два идеальных низкочастотных сигнала смещенных во времени друг относительно друга на время , таким образом, чтоб их скалярное произведение равнялось нулю.

Рассмотрим два идеальных НЧ-сигнала и . Они оба имеют спектральную плотность , и ограничены по верхней частоте . Однако сигнал запаздывает на время относительно сигнала , так, что

Обратное преобразование Фурье от скалярного произведения этих сигналов вычисляется через их спектральные плотности.

Скалярное произведение этих двух сигналов в чистом виде будет выглядеть так.

Скалярное произведение обращается в ноль и два НЧ – сигнала становятся ортогональными друг к другу при условии .

где

Данное условие означает,то = .

Минимальный дискретный сдвиг между двумя идеальными НЧ- сигналами будет равен

Таким образом, путем задержки во времени ряда сигналов друг относительно друга удалось добится не просто скалярного произведения, а создать семейство ортогональных функций, которое можно использовать для разложения сигналов в обобщенный ряд Фурье, при условии, что данные сигналы имеют ограниченный по частоте спектр.

Полученный результат формулирует основное положение Теоремы Котельникова, которая доказывает, непрерывный сигнал практически точно восстанавливается на основе его дискретных отсчетов, при условии, что дискретизация происходит с определенным шагом .