1.Определители, свойства, вычисление.

Определитель (детерминант), матрица (А) = =a1b2-a2b1, называется число равное разности произведений элементов, лежащих на главной и побочной диагоналях.

Обозн: ▲, IAI, D.

Определ-ль 3го порядка.

= + +

1)Существует удобная схема для вычисления определителя третьего порядка:

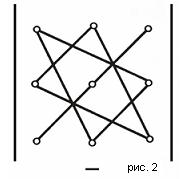
2)правило Саррюса:

Дописывание двух первых строк или столбцов.

В этом случае считаем так: a11*а22*а33 + а12*а23*31+а13*а21*а32 — а13*а22*а31 — а11*а23*а32 — а12*а21*а33.

3) разложение по строке:

, ,

Определ-ль n-го порядка им n строк и n столбцов.

Свойства определителей: 1)если у опред-ля произвольная строка (столбец) состоит только из нулей, то опред-ль =0; 2)если производные 2 строки (столбца) опред-ля пропорциональны, то опред-ль = 0; 3)если произ строку (столбец) опред-ля умножить на производное число, то и весь опред-ль умн-ся на это число; 4)если 2 строки (столбца) опред-ля поменять местами, то опред-ль изменит знак;5)если к произв строке (столбцу) опред-ля прибавить любую другую строку (столбец), умноженную на проиводн число, то опр-ль не изм-ся; 6)опред-ль произведение матриц = произведению их опред-лей.

Матрица, опред-ль котор =0,назыв вырожденной; опред-ль котор 0,назыв невырожденной.

2.Матрицы. Виды матриц. Действия над матрицами. Вычисление обратной матрицы. Ранг и его вычисление.

Матрица - -ная табл чисел, содержащая m-строк и n-столбцов.

А= , A =(aij), i=1,2,3…m- № строки, j=1,2,3…, j - № столбца.

Числа aijназыв эл-тами матрицы А. Элементы, стоящие на диаг-ли, идущ из левого верхн угла, образ главнуюd.

Матрицы равны м/усобой, если все соотв-щие эл-ты этих матриц=. А=В, aij=bij.

Матрица, у котор число строк =числу столбцов, назывквадратной.

Квадратная матрица, у котор все эл-ты, кроме эл-товглd, =0, назывдиагональной.

Диагональная матрица, у которкажд эл-т глd=1, назывединичной.

Квадратная матрица назывтреуг-ной, если все эл-ты, располож по одну сторону от глd, =0.

Матрица, все эл-ты котор =0,назыв нулевой.

Матрица, содержащая 1 столбец или строку, назыввектором.

Матрицаполуч из данной заменен производной ее строки столбцом с тем же №, назыв транспонированной.

Пример: А= , = .

Св-во: ( )Т = А.

Действия над матрицами.

1)суммой матриц А и В одинакового размера назыв М. С того же размера, причем сij=aij+bij.

1.коммуникативность:.А+В=В+А.

2.ассоциативность: ( А+В)+С=А+(В+С)=А+В+С.

2)произведением М. А на число λназыв М. В того же размера, что и М. А, причем эл-ты М. bij=λaij,Ɏλ, Ɏij.

1.λ(µА)=(λµ)А (ассоц-ть)

2.λ(А+В)=λА+λВ (дистрибутимость)

3.(λ+µ)А=λА+µА.

3)линейной комбинацией матриц А и В одного размера назыв выражение вида αА+βА, где α и β –любые числа.

4)произвед-ем м-ц А и В р-ров (мхn и nxr) назыв М. С такая что Сij=ai1*b1j+ai2*b2j+…aik*bkj+…+ain*bnj

Элементарные преобразования.

1)перемена местами 2х строк(столбцов)

2)умножение строки(столбца) на число, отлично от 0.

3)прибавление к элементам одной строки (столбца) соотв эл др строки(столбца).

Матрица Вназыв эквивалентной М.А. В .

Обратная матрица.

Обр м-ца -такая м-ца, котор в произв с данной м-цей А дает единицу и наоборот. А* =Е.

Если опред-ль =0, то квадр м-ца не им обратной и назыв вырожденной.

Если опред-ль ≠0, то обр м-ца не им обратной , Aij-м-ца алгебр дополнений, соотв эл-тов М.А.

Схема нахождения обр. мат-цы:

1)вычисляем опред-ль М.А, опред-ль≠0

2)находим м алгебр-ких дополнений Аij

3)транспонир-ть м.Aij и получить ij

4)находим м по формуле: ,

5)проверка: *А=Е, А* =Е.

Ранг матрицы.

Минором некоторого эл-та aijопред-ляn-го порядка назывопредел-ль (n-1) порядка, которполуч из исходного путем вычеркивания строки и столбца, на пересечение которых находится выбран эл-т

Mij – минор для эл.

, М22= , М13= , M23= .

Опред-ние

Алгебраич дополнением будет назыв-сяпроизв-ние i-№ строки, j-№ столбца.

Наиб из порядков миноров данной м-цы, отличных от 0, назыврангом м-цы.

Обозн: r, r(A), rang (A)

Минор, порядок которопредел-ет ранг м-цы, назывбазисным.