5.Введение мерак по измерению величин. Моделирование величин отрезками. Измерение отрезков меркой и появление последовательности целых неотрицательных чисел..
. . . . . . . . . . . мерка
0 1 2 3 4 5
Уменьшим мерку в 2 раза: новая мерка
6. Переход к меньшей мерке и введение действия умножения.
. . . . . . . . . . .
0 1 2 3 4 5 6 7 8 9 10 5•2=10
7. Переход от меньшей к большей мерк и введение действия ДЕЛЕНИЯ : 10 : 2 = 5.
8. С помощью моделирования и перехода к меркам в 10 раз больших (меньших) за данную вводятся также десятичные дроби, проценты и действия над ними.
Теперь рассмотрии учебные задачи по программе 2100
Сначала выделяется всеобщее отношение. Такими отношениями для математик может быть отношение: «часть – целое». Оно является исход-ной «клеточкой» построения системы учебных задач. Вначале изучаются свойства предметов: цвет, форма, размер. Учащиеся выполняют самостоятельные задания на выделение указанных свойств предметов, на установление сходства и различия предметов по определён-ному свойству, на обобщение, аналогию и классификацию предме-тов по этому свойству.
Затем учащиеся рассматривают совокупности предметов, обладающих общими признаками, на основе объединения предметов и выделения части их из целой совокупности по определённому свой-ству.
Наконец, решается учебная задача: Как по представленным множествам, а затем и по их мо-делям найти соотношения «целого и его частей»? Из множества-модели выделяются операции, служащие основой для введения понятий сложе-ние и вычитания целых чисел и вводятся услов-ные обозначения: квадрат -- К, прямоугольник – П, геометрическая фигура -Ф, «+» плюс – прибавить. « - » минус -вычесть, «=» равно.
К + П = Ф 4 + 2 = 6 По
П + К = Ф 2 + 4 = 6 фор-
Ф - К = П 6 - 4 = 2 ме
Ф - П = К 6 - 2 = 4
Делаются выводы: 5 + 1 = 6 По
- ЦЕЛОЕ ЕСТЬ СУММА ЧАСТЕЙ 1 + 5 = 6 раз-
- ЧТОБЫ НАЙТИ ЧАСТЬ, НАДО 6 - 1 = 5 ме-
ИЗ ЦЕЛОГО ВЫЧЕСТЬ ДРУГУЮ ЧАСТЬ 6 - 5 = 1 рам
- ЦЕЛОЕ – это сумма , уменьшаемое. 3 + 3 = 6 По
ЧАСТЬ –это 1-ое или 2-ое слагаемое, разность 6-3=3 цвету Одновременно с этим эти действия показывают на числовом луче.
! ----!---!--- !----!---!----!---!----!--------------------
0 1 2 3 4 5 6 7 8
В водится понятие о задаче и оформляется структура её на схеме
У СЛОВИЕ: У Тани , у Саши .
ВОПРОС: Сколько грибов у Тани и Саши вместе?
С ХЕМА: Т = 4 С= 2
Т и С ?
ВЫРАЖЕНИЕ: 4 + 2
РЕШЕНИЕ: 4 + 2 = 6 ( гр.)
ОТВЕТ: У Тани и Саши было 6 грибов.
По другим схемам ученикам предлагается сос-тавить задачи, обратные данной.
Т ?
С= 2 Т = 4 С ?
Т и С 6 Т и С 6
После решения простых предлагается самос-тоятельно решить по схемам составные задачи: У Маши, Тани и Кати 8 марок. У Маши 2 марки, а у Тани 3 марки. Сколько марок у Кати?
? 8 8
М Т К М Т К М Т К М Т К !-----!-------!------! !------!-------!------! !-------!------!-------! !-------!-------!----
2 3 ? 2 3 3 2 ? 3 ? 3 3
При изучении операций умножения и деления используется модель - прямоугольник. По ней на-ходится площадь (П) по длине (а) и ширине (в).
а
а · в = П 6 · 3 = 18
3см П в в · а = П 3 · 6 = 18
П : а = в 18 : 6 = 3
6 см П : в = а 18 : 3 = 6
В дальнейшем найденный общий способ реше-ния задачи применяется при решении других задач данного класса на действия умножения и деления.
Рассмотрим теперь теоретико-множествен-ный подход к решению простых залач, принадлежащий СтоляруА.А.
Теоретико-множественной основой ЗАДАЧ НА СЛОЖЕНИЕ целых неотрицательных чисел (ЦНЧ) чвлчется операция объединения А В=С конечных непересе-кающихся множеств. Пусть количество элементов множеств
п(А)=п{х,х,х}=3, п(В)=п{о,о}=2, тогда
п(С)=5, п(А В)=п{х,х,х,о,о}=3+2=5. Теоретико-множественной основой ЗАДАЧ НА ВЫЧИТАНИЕ является операция разности множеств С\А или С\В, где А С и В С.Тогда п(С\А)=5-3=2 и п(С\В)=5-2=3. . Теоретико-множественной основой ЗАДАЧ НА УМНОЖЕНИЕ ЦНЧ является произ-ведение: 1) а•в=а+а+а+...+а (в раз), 2) а•1=а, 3)а•0=0.
Теоретико-множественной основой ЗАДАЧ НА ДЕЛЕНИЕ ЦНЧ является разбиение множества А={х,х, о,о, *,*}, где п(А)=6,
на равночисленные подмножества:
--если получим равное количество элемен-тов каждого подмножества 6:3=2, то это будет ДЕЛЕНИЕ НА РАВНЫЕ ЧАСТИ
если получим количество частей 6:2=3, то это будет ДЕЛЕНИЕ ПО СОДЕРЖА-НИЮ.
ОСНОВНЫЕ ЭТАПЫ
КОНСТРУИРОВАНИЯ ТЕСТОВ
1. Определить цели тестирования, выбор подхода
к созданию и проверке теста.
2. Анализ содержания учебной дисциплины.
3. Определение структуры теста,форм
заданий, расположения заданий в нём.
4. Выбор длины теста и времени его выполнения.
5. Создание тестовых заданий.
6. Ранжирование заданий в тесте.
7. Экспертиза содержания и формы
тестовых заданий.
9. Переработка содержания и формы заданий
теста по результатам экспертизы.
10. Разработка методики апробационного
тестирования.
11. Разработка инструкций для учеников и для
преподавателей по процедуре тестирования.
12. Проведение апробационного исследования.
13. Сбор эмпирических материалов.
14. Статистическая обработка результатов
выполнения теста.
15. Интерпретация результатов обработки
предтеста в целях улучшения его качества.
16. Коррекция содержания и формы заданий.
17. Создание шкалы для оценки результатов испытуемых по тесту, перевода баллов теста в школьные отметки.
ТРЕБОВАНИЯ К ЗАДАНИЯМ С
МНОЖЕСТВЕННЫМИ ОТВЕТАМИ
1. Избегать неопределённости, двусмысленности и
неясности в формулировках заданий теста.
2. Задания формулировать кратко в виде
предложений с не более, чем 7-8-ью словами.
3. В предложение задания включать не более
одного придаточного предложения.
4. Ответы должны быть предельно краткими.
Повторяющиеся в них слова следует включать
в основную часть теста.
5. Все ответы должны иметь приблизительно
одинаковое количество слов. Правильный
ответ может быть короче неправильных.
6. Номера правильных и неправильных ответов
(дистракторов) следует часто менять.
7. Все дистракторы должны быть правдоподоб-
ными, равнопривлекательными, не подсказы-
вающими ответ по ассоциации с другими.
8. Дистракторы и правильные ответы не должны
быть частично правильными, неработающими.
9. Ответ на задание не должен служить ключом к
правильным ответам на другие задания.
10. Исключать из заданий оценочные суждения,
чьи-либо мнения, слова некоторые,не всегда.
Практикуются также фасетные, т.е. многова-риантные задания, которые могут выбираться учениками по их желанию или желанию учителя. Трудность каждого задания определяется по количеству ошибок, допущенных учащимися. Задание считается тем труднее, чем большее количество ошибок по нему допускают школьники. В тесте должно быть не менее 10-15 заданий.
Сначала тесты проверяются высококва-лифицированными специалистами-экспертами, затем они проходят опытную проверку в разного типа школах. Результаты тестирования тщательно анализируются с применением мето-дов математической статистики. С учётом соб-ранных замечаний тесты совершенствуются, стандартизируются.
Таблица результатов тестирования 1
Номер ис- пытуемого і |
Н о м е р з а д а н и я j |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
1 |
0 |
0 |
0 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
4 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
5 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
6 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
7 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
8 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
10 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
12 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
С предтеста часто снимают задания: с 11 строчки таблицы как очень лёгкие и с 12 строчки как очень трудные. Проводится ранжирование данных таблицы.
Проранжированная и скорректированная таблица 2
№ исп. І |
Н о м е р з а д а н и я j |
Инд.балл хі |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
2 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
5 |
1 |
0 |
1 |
0 |
1 |
1 |
0 |
0 |
0 |
0 |
4 |
6 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
4 |
8 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
7 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
5 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
6 |
10 |
1 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
6 |
9 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
9 |
4 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
9 |
Пр.отв. |
9 |
8 |
7 |
6 |
5 |
5 |
4 |
3 |
2 |
1 |
50 |
Таблица несгруппированного ряда 3
№ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
Балл |
6 |
2 |
1 |
9 |
4 |
4 |
5 |
4 |
9 |
6 |
Таблица ранжированного ряда 4
Ранг |
1 |
2 |
3 |
3 |
3 |
4 |
5 |
5 |
6 |
6 |
№ |
3 |
2 |
5 |
6 |
8 |
7 |
1 |
10 |
4 |
9 |
Балл |
1 |
2 |
4 |
4 |
4 |
5 |
6 |
6 |
9 |
9 |
Таблица частотного распределения 5
Балл |
1 |
2 |
4 |
5 |
6 |
9 |
Частота |
1 |
1 |
3 |
1 |
2 |
2 |
Машинописный график 6
-
---------------------------------------------------------------------
Баллы ! 1 2 3 4 5 6 7 8 9
----------------------------------------------------------------------
График ! Х ХХ ХХХ Х ХХ ХХ
Таблица сгруппированного частотного распределения 7
Интервалы баллов |
Частота |
1 - 3 |
2 |
4 - 6 |
6 |
7 - 9 |
2 |
Таблица 8 перевода полученных баллов по тесту с Т- шкалы в школьные отметки по 10-балльной системе
№ От- Метка |
Н о м е р з а д а н и я j |
хі |
хі-Х |
Zі |
|||||||||
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
||||
3 ! 3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
0 |
0 |
1 |
- 4 |
-1,54 |
2 ! 4 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
- 3 |
-1,14 |
5 ! 5 |
1 |
0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
0 |
4 |
- 1 |
- 0,38 |
6 ! 5 |
1 |
1 |
1 |
0 |
0 |
0 |
1 |
0 |
0 |
0 |
4 |
- 1 |
- 0,38 |
8 ! 5 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
- 1 |
-0,38 |
7 ! 6 |
1 |
1 |
1 |
1 |
0 |
1 |
0 |
0 |
0 |
0 |
5 |
0 |
0 |
1 ! 7 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
0 |
0 |
6 |
1 |
+0,38 |
10 ! 7 |
1 |
1 |
1 |
1 |
1 |
0 |
0 |
1 |
0 |
0 |
6 |
1 |
+0,38 |
9 ! 9 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
0 |
9 |
4 |
+1,54 |
4 ! 9 |
1 |
1 |
0 |
1 |
1 |
1 |
1 |
1 |
1 |
1 |
9 |
4 |
+1,54 |
в 10-б. |
9 |
8 |
7 |
6 |
5 |
5 |
4 |
3 |
2 |
1 |
50 |
0 |
Z= 0 |
Для
оценки качества предтеста применяются
методы математической статистики. В
частности, используются меры центральной
тенденции: среднее арифметическое, мода
и медиана. Среднее
арифметическое
получен-ных баллов:
=
(1+2+4+4+4+5+6+6+9+9):10=50:10=5.
Наиболее часто встречающийся балл (мода): Мо = 5.
Середина упорядоченного ряда баллов, которые стоят на 5 и 6-ом месте (медиана) : Ме = (5+6):2 = 5,5.
Определяют также отклонение каждого балла от Х. Вычитают из каждого балла Х , а затем каждую раз-ность возводят в квадрат и результаты складывают.
(1-5), (2-5), (4-5), (4-5), (4-5) (5-5), (6-5), (6-5) ,(9-5) (9-5).
-4, -3, -1, -1, -1, 0, +1, +1, +4, +4.
16, 9, 1, 1, 1, 0, 1, 1, 16, 16.
16 + 9 + 1 + 1 + 1 + 0 + 1 + 1 + 16 +16=
= 62. Эту сумму полученных квадратов делим на 10-1=9. Получаем σ2 = 62 :9 ≈ 6,89 - среднее квадра-тичное отклонение или дисперсию. Более подробно: (1-5)2 + (2-5)2 + (4-5)2 + (4-5)2+ (4-5)2 + + (5-5)2+ (6-5)2 + (6-5)2 + (9-5)2+ (9-5)2 = 62. σ2 = 62 : 9 ≈ 6,89.
Извлекая квадратный корень из дисперсии 6,8,получаем приблизительно σ = 2,6.Это стандартное отклонение.
Размах определяется как разность между наиболь-
шим и наименьшим баллом: 9-1= 8.
Формулы среднего арифметического Х, отклонений от него числовых данных хі::
-
среднее арифметическое
-
дисперсия
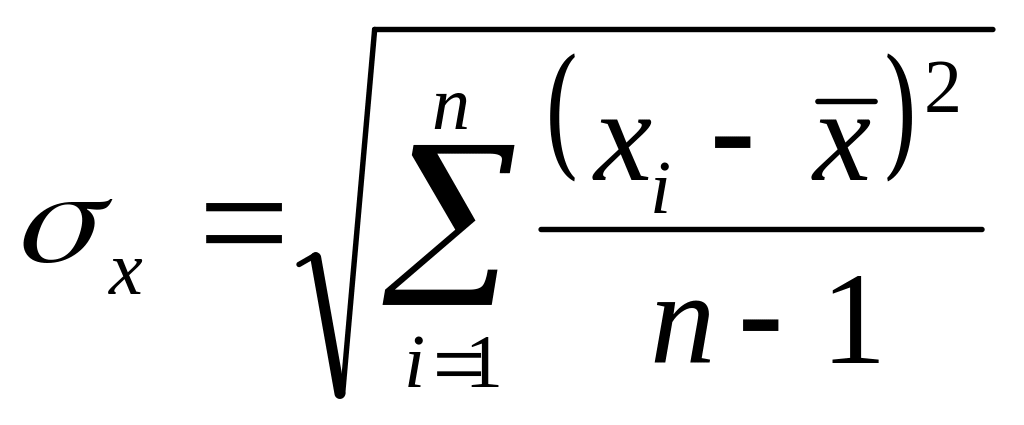n
- количество числовых данных
Если среднее арифметическое, мода и медиана рав-ны или приблизительно равны, то распределение (про-ранжированный ряд баллов теста с указанием количес-тва каждого балла) называют нормальным распределе- нием. Его график имеет вид колоколобразной кривой.
При корректировке результатов предтестов приходится их графическое представление всё время сравнивать
с
этой кривой График 1.
Нормальное нулевая ассиметрия
распределение
График
2
График
3
у
отрицательная
положительная
ассимметрия
Таким образом степень отклонения распределения от нормального распределения оценивается с помощью ассиметрии. Визуально это можно проследить : на графике 1- нормальное распределение с нулевой, на графике 2 - распределение с отрицательной и на графике 3 - с положительной ассиметрией.
С помощью эксцесса на графике в виде полигона или гистограммы можно проследить его островершин-ность (положительный эксцесс) или его пологость - ( отрицательный эксцесс)
Т Е С Т
Что вы знаете о задачах? Умеете ли их решать?
1. Подчеркните условие задачи одной чертой, а вопрос
двумя чертами: Когда отцу было 37 лет, сыну было 3
года, а сейчас сыну в 3 раза меньше, чем отцу.
Сколько лет отцу?
2. Допишите слова. Задача - это цель в______ ______ .
3.Соедините нужные выражения столбцов стрелками
Предметная область 37 лет
Величина задачи настоящий возраст отца
Известные значения время
Неизвестные значения в 3 раза меньше
Отношение задачи настоящий возраст сына
Искомое значение 3 г
4. Дополните по тесту задачи её:
краткую запись…………………………………………
чертёж……………………………………………………
5. Запишите слова начала разбора задачи способом :
аналитическим ……………………………………………… синтетическим…………………………………………......
6. Запишите ответ и решение задачи :
по действиям ………………………………………………
.составлением выражения............................................
7. Сделайте проверку решения разными способами........
8. Решите задачу другими способами...............................
9. Начертите граф-схему разбора задачи.......................
10.Запишите аналогичную задачу...............