2.5. Умовна ентропія

Припустимо, що повідомлення а зустрічалося у довгому лан­цюзі з N = 1000 повідомлень І_х = 200 разів, повідомлення Ь у цьому самому ланцюзі — /₂ = 200 разів, а разом вони зустрілися лише /₃ = 50 разів. Скориставшись теорією математичної ста­тистики, можна встановити, що ймовірність появи повідомлення а в цьому ланцюзі р (а) = l_xIN = 0,25, а повідомлення b-p(b) = = l₂IN = 0,2. Крім того,/? (ab) - l₃/N = 0,05. При цьому/? (ab) =

34

*■ р (а)р Ф) = 0,25 • 0,2 = 0,05, що є явною ознакою статистичної иешлсжності повідомлень а та Ь. Саме для таких повідомлень {смуг безумовна ентропія, про яку йшлося вище.

Коли б у цьому прикладі пара ab зустрілася /₃ = 30 разів, то ииянилося б, що р (ab) = l₃IN = 0,03 < р (а) р (Ь). Це є ознакою порушення статистичної незалежності повідомлень а та Ь, яка відбиває той факт, що вони не «прагнуть» зустрічатися разом у послідовностях повідомлень, тобто поява одного з них дає підставу з більшою впевненістю не очікувати появи іншого, ніж не було б до появи першого повідомлення. Це означає, що ймо­вірність появи, скажімо, повідомлення b в послідовності відра-іу після появи повідомлення а трохи зменшується, і навпаки, хоча взагалі безумовна ймовірність/? (а) чи/? (Ь) по всій послі-доііпості в цілому є сталою.

і іншого боку, при /₃ = 100 маємо/? (ab) = l/N = 0,1 >/? (а)р (b), ₍|цо даг підставу підозрювати взаємне «тяжіння» а до Ь, і навпа­ки. Ту і теж проглядається порушення статистичної незалеж­ності, тобто відношення «байдужості» між повідомленнями а Ті Ь. Поява в послідовності одного з них, наприклад а, трохи 'іґшімнуг ймовірність появи повідомлення b відразу за повідом­ленням а_% і навпаки. Проте безумовні ймовірності/? (а) тар (Ь) по послідовності в цілому теж є сталими.

Мірою порушення статистичної незалежності (стану «бай­ дужості») між повідомленнями а та £ є умовна ймовірність по­ ний повідомлення а за умови, що вже з'явилося повідомлення b p {alb), або умовна ймовірність появи повідомлення Ь, коли »«• нїлося повідомлення а: р (Ь/а), причому взагалі/? (alb) Ф

і і математичної статистики визначає умовну ймовір-

«• м .-и | >сз безумовні ймовірності/? (а),р (Ь) та сумісну безумов-и і імовірність/? (ab) за законом множення ймовірностей:

р (ab) =p(a)p (bla) =p(b)p (alb). (2.13)

Звідси випливає, що

р (bla) = p (ab) /p (a); p (alb) = p (ab) Ip (b). (2.14)

Зокрема, для статистично незалежних повідомлень а та b (див. вище) маємо

р (bla) = 0,05 / 0,25 = 0,2 = /? (b);

р (alb) = 0,05 / 0,2 = 0,25 = р (а),

міно умовні ймовірності появи повідомлень вироджуються в

І" і УМОВНІ.

35

Тоді для /₃ = ЗО згідно з (2.14) знаходимо

р (Ь/а)= 0,03/0,25 = 0,12;/? (alb) = 0,03/0,2 = 0,15, (2.15)

тобто встановлений факт появи повідомлення а зменшує безу­мовну ймовірність р (Ь) = 0,2 до умовної ймовірності р (Ыа) = = 0,12 появи повідомлення b за умови наявного вже повідом­лення а. І навпаки, факт появи повідомлення b зменшує безу­мовну ймовірністьр (а) = 0,25 до умовної ймовірності/? (alb) = = 0,15 появи повідомлення а за умови наявності повідомлення Ь. Як бачимо, ймовірність появи повідомлення b зменшується на 0,08, а повідомлення а — на 0,1 кожного разу, як інше з них з'явиться в послідовності.

Аналогічно стосовно наведеного вище прикладу з /₃ = 100 відповідно до (2.14) маємо

р (Ыа) = 0,1/0,25 = 0,4; р (alb) = 0,1/0,2 = 0,5, (2.16)

що підкреслює згадане вище «тяжіння» а та b одне до одного через підсилення ймовірностей появи їх.

Насправді, при безумовній імовірності, скажімо,/? (Ь) = 0,2 (саме з такою ймовірністю джерело вибирає b серед інших мож­ливих повідомлень у довгому їх ланцюзі), як тільки буде виб­рано а₉ ймовірність вибору b слідом різко (вдвічі в розглядува­ному прикладі) підсилюється до значення умовної ймовірності /? (Ыа) = 0,4 появи повідомлення b за умови наявності повідом­лення а. І навпаки, при/? (а) = 0,25 взагалі, як тільки буде виявле­но повідомлення b , ймовірність появи повідомлення а слідом або поряд з b різко підсилиться до значення умовної ймовірності /? (alb) = 0,5 згідно з (2.16). Отже, при виявленні одного повідом­лення ймовірність появи слідом або поряд із ним статистично зумовленого, зв'язаного повідомлення збільшується [для умов (2.16)] або зменшується [для умов (2.15)].

Ці локальні порушення ймовірностей при статистичній залеж­ності повідомлень не можуть бути непоміченими джерелом. І воно на них реагує відповідним зменшенням або збільшенням кількості інформації в кожному такому повідомленні згідно з (2.5). Звісно й ентропія такого джерела має змінюватися належним чином, причому називається вона умовною, визначається виразом (2.6), але з урахуванням умовних імовірностей повідомлень.

Розрізняють два різновиди умовної ентропії: часткову та загальну. Першу знаходять так:

H(Albj) = ^p(a_ilbj)\ogp(a_ilb_J)J = \.J; (2.17)

^{z rf/}H(Bla_i) = -Zp(bjla_i)\ogp(bjla_i)J = l...k, (2.18)

J 36

пс А = {a_]9a₂₉...₉a_i9...₉a_k}₉B = {b_{9b₂₉ ...₉b_j9 ...,£,} —алфавіти повідомлень; а_і — конкретне повідомлення, відносно якого ви-іначається часткова умовна ентропія Н (ВІа) алфавіту В за умови вибору попереднього повідомлення а;₉ bj — конкретне повідомлення, відносно якого обчислюється часткова умовна ентропія Н (А/Ьр алфавіту А за умови вибору попереднього повідомлення b»•; / — номер повідомлення з алфавіту A;j— но­мер повідомлення з алфавіту В; р (alb), р (Ыа) — умовні ймовір­ності.

Термін «вибір попереднього» досить умовний, оскільки по­відомлення а та b можуть бути рознесені в часі, але знаходити­ся разом у просторі (як записано вище alb чи Ыа), або бути од­ночасними чи майже одночасними та рознесеними в просторі (як на рис. 2.1). Ніякі обмеження на алфавіти А та В не накла­даються. Вони можуть навіть збігатися (А = В). Тому можна аналізувати і враховувати взаємозв'язок між повідомленнями одного й того самого джерела в одному й тому самому алфавіті повідомлень, рознесеними в часі, але не в просторі (наприклад, на виході джерела А чи В згідно з рис. 2.1). Такі послідовності іумовлених повідомлень називаються ланцюгами Маркова [38, 46, 49].

З іншого боку, алфавіти А та В можуть не збігатися (А Ф В), хоча між елементами їх може бути й відповідність. Цю ситуа­цію відбито на рис. 2.1, де джерело А має свою модель — ан­самбль Атг.Р_А. Оскільки воно може мати к дискретних станів, джерело А виступає як об'єкт спостерігача В і разом із ним утво­рює нове джерело В, яке має свою модель — ансамбль В та Р_в. Між джерелом А та спостерігачем В існує канал зв'язку, в яко­му діють, умовно кажучи, завади, що порушують процес вибору спостерігачем В повідомлень Ь- є В. Це, в свою чергу, порушує відповідність між повідомленнями а_і є А та 6. є В.

Алфавіти АтаВ можуть бути однакового (к = І) і неоднако­вого (к Ф І) обсягів. Звичайно розглядають ситуації, коли к - І ибо к < І. Система спостереження зк = 1 має природне пояснен­ня. Тут спостерігач В повинен реагувати своїм повідомленням b_f (і = 1 ... І) на кожний стан джерела А, висловлений повддомлен-нмм а. (і = 1 ... к). При цьому діє принцип перетворення а_{ —> Ь_[9 <h ~» Ь₂, ..., а і —> Ь_і9 ..., а_к —> Ь_к, коли кожному повідомленню а_і джерела А відповідає повідомлення b₍ джерела В. Цю модель юбражено на рис. 2.4, за винятком елемента b_l із В, де / = к + 1. Ma рисунку виділено напрямки взаємооднозначної відповідно-і\\А<=>В.

Як вгадувалося вище, завади порушують вибір повідомлень h_f джерелом В. За цих обставин, якщо джерелом А вибрано пев-мг повідомлення а_і9 якому має відповідати повідомлення Ь- при

37

Завади j = /, TO ДЖЄрЄЛО В МОЖЄ Вибрати

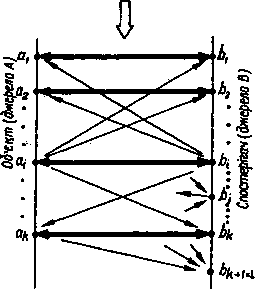
будь-яке повідомлення bj при j = = 1 ... А:з імовірністю/? (bj/a), при­чому умовна ймовірність правиль­ного вибору (тут воно має смисл перетворення а_і -> Ь) дорівнює р (b_tla). Решта виборів будуть по­милковими з умовними ймовір­ностями р (bj/a) при j Ф і. Це дає змогу дослідити систему спостере­ження, передачі, перетворення, збирання, збереження інформації з боку спостерігача В.

Рис. 2.4

Водночас таку систему можна дослідити з позицій спостерігача В. Для цього потрібно знати факт вибору джерелом В певного повідомлення bj. Після встанов­лення такого факту можна з умовною ймовірністю/? (я/6) ска­зати, що об'єкт А знаходиться в стані а_г Це твердження може бути правильним при / =j або неправильним при / Ф].

Існують певні ситуації, за яких систему доводиться ускладню­вати, вибираючи / > к (частіше / = к + 1, див. рис. 2.4). При цьому повідомлення Ь[ не відповідає ніякому повідомленню а_і (і ФІ),з.є ознакою та повідомленням про особливий стан спостерігача В, який відмовляється від вибору якогось певного повідомлення bj (j = 1 ... к) у відповідь на повідомлення я,- (і = 1 ... к). Цей стан спостерігача називається стиранням повідомлення. Відбувається воно з умовною ймовірністю/? (Ь^а), якщо стан я_;. джерела А ві­домо. Якщо ж, навпаки, відомим є стан стирання повідомлення bf джерела В, то з умовною ймовірністю/? (я/6/) можна вважати, що джерело А знаходилося в стані я.. Коли ж / = 1 ... к тау' = 1 ... ... к, все відбувається аналогічно вищерозглянутій моделі без Ь_{ = = Ь_к+Х у складі джерела В, тобто коли / = к.

Згадаємо ще також про те, що крім статистичного зв'язку між парами повідомлень у довгих послідовностях (рознесення в часі) або в складених системах (рознесення в просторі) часто спостерігається статистичний зв'язок між трьома, чотирма й більше повідомленнями, що зумовлює наявність умовної ентро­пії більш високого порядку [3, 42].

Тепер повернемося знову до часткової умовної ентропії і будемо дотримуватися моделі системи спостереження, показаної на рис. 2.4 без стирання, тобто коли / = к. Звернемося до фізичного змісту умовної ентропії. Як і при визначенні безумовної ентропії, часткова умовна ентропія є математичним сподіванням значення р (а₍/Ьр або/? (bj/a). Це поняття відбиває середню за повним алфа-

вітом кількість інформації, що припадає на одне повідомлення цього алфавіту (джерела). Тому Н (АІЬр в (2.17) є питомою кіль­кістю інформації джерела А за умови, що вже встановлено, факт вибору джерелом В певного повідомлення bj, H (В/а) в (2.18) — питомою кількістю інформації джерела В за умови, що вже відо­мо стан джерела А. Іншими словами, Н (Alb) — це середня кіль­кість інформації, яка містилася в будь-якому повідомленні дже­рела А, якщо джерело В вибрало повідомлення bj (j = 1 ... к), а Н (В/а) — середня кількість інформації, здобутої після вибору джерелом В будь-якого свого повідомлення, коли відомо, що дже­рело А знаходилося в стані я_; (/ = 1 ... к). Часткова умовна ентро­пія визначається як статистичне усереднення за методом зваже­ної суми (2.17), (2.18) по індексу і= 1 ... А:абоу= 1 ...& відповідно. Ураховуючи викладене вище, загальну умовну ентропію можна визначити так: якщо часткова умовна ентропія джерела А відносно конкретного повідомлення bj дорівнює Н (Alb), a розподіл імовірностей Р_в джерела В задано ансамблем Візг_в = = {р (Ь\\ .-,/? (Ь), ...,/? (Ь_к)}, то цілком природно обчислити середнє по j значення Н (A/bj) за всіма у як статистичне усеред­нення методом зваженої суми, тобто

H(A/B) = Zp(bj)H(A/bj), (2.19)

J де Я (А І В) — загальна умовна ентропія джерела А відносно

джерела В. Це питома (середньостатична) кількість інформа­ції, що припадає на будь-яке повідомлення джерела А, якщо відомо його статистичну взаємозалежність із джерелом В.

Аналогічно (2.19) загальна умовна ентропія джерела В від­носно джерела А визначається виразом

Н(ВІА) = ^р(а_і)Н(В/а_і), (2.20)

і

що є питомою (середньостатичною) кількістю інформації, яка припадає на будь-яке повідомлення джерела В, якщо відомо його статистичну взаємозалежність із джерелом А.

Вирази (2.19) і (2.20) є операціями згортки за індексом, внаслі­док якої операція (2.19) «поглинає» індексу, а операція (2.20) — Індекс і.

З урахуванням (2.13), (2.17), (2.18) вирази (2.19) і (2.20) набу­вають вигляду

H(A/B) = -Zp(bj)Zp(a_i/bj)\ogp(a_i/b_J) =

j і

= -2 S P(bj)P(<*i I bj) log p(a • /bj)= (2.21)

= -llp(a_i/bj)\ogp(a_i/b_j);

J і

38

39

р(а_хІЬ_х) р(а_х/Ь₂) ... p(a_x/bj) ... р(а_х/Ь_к)

■ . р(а₂ІЬ_к)

(2.22)

(2.23)

ЩВІА) = -ЇРІа^рЩ la_t)togp{bj Ч,) =

• J

^-TLPifiilbnbgpibjIa,).

' J

Р(В/А) =

Загалом статистична залежність джерела В від джерела А від­бивається матрицею прямих переходів повідомлень а_і (і = 1 ... к) джерела А в повідомлення Ь- (/ = 1 ... А:) джерела В:

А	"~ в
	Ь\ 1 *>2 І"- | bj 1-І 6*
в, \а2 \аі	р(Ьх1а^ р(Ь2Іа{) ... pibjla^ ... /> (Vai)|
	р (6,/а2) pjfij/a^ ... p(bjla2) ... р(ЬкІа2)\ рф./а) рЩа) ... р (bj/a,) ... РФкШ РФМ) рФ21ак) ... р(Ь/ак) ... р (Ьк1ак)\

На головній діагоналі цієї матриці розміщено умовні ймовір­ності прямої відповідності типу а_х —> 6,, ..., а_к —> Ь_к, які харак­теризують правильний вибір джерелом В своїх повідомлень (тобто відповідно до повідомлень джерела А). Решта ймовір­ностей відповідають неправильному вибору повідомлень дже­релом В.

Матриця (2.23) відбиває вплив завад у каналі між джерелом А та спостерігачем В (див. рис. 2.1). Якщо завади непомітні або зовсім відсутні, то маємо однозначну відповідність а₍ —> Ь_{ з умов­ної ймовірності р (Ь^а,) = 1 для / = 1 ... к. Решта ймовірностей р (bJaj) = 0 для всіх j Ф і.

Кожний рядок у (2.23) є спотвореним розподілом імовірнос­тей Р_в появи повідомлення bj є В. Джерело В має розподіл без­умовних імовірностей Р_в. Врахування статистичного впливу повідомлення а і є А спотворює цей розподіл (або уточнює його) і дає новий розподіл імовірностей Р (2?/д,) для /-го рядка матри­ці. Саме тому виконується закон нормування

j Статистична залежність джерела А від джерела В відбива­ється матрицею зворотних переходів типу а_{ <— Ьр складеною з умовних імовірностей р (ctj/b):

40

Р(А/В) =

р(а,/Ь_к) . р(а_кІЬ_к)

p(a₂/b_x) p(a₂/b₂) ... p(a₂/bj) р{а])ь_х) p(a_i)b₁) ... Piajbj)

(2.25)

[р(а_к lb_x) p{a_klb₂) ... р(а_к /bj) . = P(Albj),i=l...k.

Вона відображає к розміщених стовпцями варіантів спотво­рених первинних розподілів імовірностей ансамблю А:, які відчу­вають на собі статистичний вплив повідомлень b_} (J' - 1 ... к), вибраних джерелом В. Саме тому для кожного такого розподілу

(2.26)

lp(a_i/b_j)^\J=l...k.

Таким чином, якщо задано ансамбль А та матрицю прямих переходів (2.23), то, враховуючи (2.13), можна знайти сумісні безумовні ймовірності р (я,, Ь) = р ф_р я,), взявши з ансамблю А безумовні ймовірності Р_А = {р (а,)}, і = 1 ... к. Виконавши згорт­ку по і, дістанемо такий розподіл безумовних імовірностей P_B=ip(bp}J=l...k:

(2.27)

p(b_J) = Yp(a_ib_jlJ=l...k.

Звідси за формулою, подібною до (2.8), визначаємо безумов­ну ентропію

Н(В) = -tpibjVogpibj). (2.28)

Звичайно, цю ентропію можна знайти безпосередньо за (2.8), скориставшись значенням/? (я,) з ансамблю А. У мовні ентропії як часткові, так і загальні можна визначити за наявними дани­ми {р (д.)}, {р (bJa)} та/?(яД). Взагалі треба виділити розподіл сумісних імовірностей Р(А,В)=[р (я,, *,)}, за яким можна діс­тати розподіл Р_в згорткою по і (2.27), або розподіл Р_А згорт­кою за j:

p(a_i)=ip(a_ib_J),i=l...k, (2.29)

7=1

після чого легко знайти розподіли умовних імовірностей для матриць (2.23) та (2.25) на підставі (2.14). Маючи ці дані, мож­на визначити всі розглянуті різновиди ентропії: Я (А) за (2.8), // (В) за (2.28), Я (АІЬ) за (2.17), Я (ВІа) за (2.18), Я (А/В) за (2.21)іЯ(/3/Л)за(2.22).

41

(2.30)

На завершення розглянемо конкретний приклад.

Нехай задано таку матрицю Р (а._у bp сумісних імовірностей появи по­відомлень двох джерел А та В (див. рис. 2.1) з алфавітами а. та Ь, де / = 1,2, Зтау=1,2,3(А; = /=3):

ОД 0

0 0,1 ОД 0,1

J 1

2. З

P(a_hbj)=

0,1 0,1 ОД

1 2 З

Оскільки р (ab) -нормування

- безумовні ймовірності, для них виконується закон

X !>(*/*/) = 1. /=іу=1

0 + | + | = | = l = p(^/6₂) + /?(a₂/6₂) + /?(a₃/^2) приу = 2;

0,25 + 0,25 + 0,5 = | = 1 = /?(д₁/6₃) + /?(а₂^з) ⁺ /⁷(^а3^/^з) ^ПР^ИУ ^{= 3}-Отже, кожний рядок (2.33) є розподілом повідомлень я., спотвореним Через статистичний вплив повідомлень be В [пор. із (2.32)]:

ОД 0 0,1

J 1

\² =

з

"2/3 0 0,25

0 2/3 0,25

1/3 1/3 0,5

0,3 0,3 0,4

p(b_j/a_i) =

(2.34)

J)_ ОД ^1_

0,3 0,3 0,4

0,1 0_?j_ ОД

L0,3 0,3 0,4 J

1 2 З

(2.31)

(2.33)

Окрема розгортка по рядках (по і) без змінну «поглинає» алфавіт а. і дає безумовну ймовірність/? (Ь), тобто ймовірнісну міру для джерела В:

0,2 + 0 + 0,1 = 0,3 = /? (£,) приу = 1; 0 + 0,2 + 0,1 = 0,3 = р ф₂) приу = 2; 0,1 + 0,1 + 0,2 = 0,4 = /? (6₃) приу = 3.

Перевіримо нормування:

р (Ь_})+р(Ь₂) +p(b₃) = 0,3 + 0,3 + 0,4 = 1.

Окрема згортка по стовпцях (за у) без зміни / «поглинає» алфавіт Ь і дає безумовну ймовірність/? (я.), тобто ймовірнісну міру для джерела А:

(2.32)

0,2 + 0 + 0,1 =0,3=/? (а,) при /= 1; 0 + 0,2 + 0,1 = 0,3 =/? (а₂) при і = 2;

0,1 + 0,1 + 0,2 = 0,4 =/? (я₃) при /: Перевіряємо нормування:

/? (а_х) + /? (я₂) + р (а₃) = 0,3 + 0,3 + 0,4 = 1. З урахуванням (2.14) на підставі (2.30) дістаємо таку матрицю умов-

них імовірностей:

0,2 0 0,1

2/3 0 1/3'	У 1
0 2/3 1/3	2
0,25 0,25 0,5	3

ojojoj

м-/^)=

0,3 0,3 0,3

од_^од

L0,4 0,4 0,4. 1 2 З

Перевірка на виконання закону нормування (2.26) дає позитивну від­повідь, тобто

І⁺⁰⁺з" ⁼ І = ¹ = Р(^а\^,ьО⁺Р(^а2^/ьО + Р(^аз^/ьО приу= 1; ,

Перевірка виконання закону нормування (2.24) дає позитивну відпо­відь, тобто

2/3 + 0 + 1/3 = З/З = 1 = р (bja) + p (b₂la_x) + p (bja) при і =1; 0 + 2/3+1/3 = 3/3 = 1=/? (bja₂) + /? (b₂/a₂) + p (b₃la₂) при і =2; 0,25 + 0,25 + 0,5 = 1 = р (Z?,/a₃) + p (bja₃) + /? ф₃/а_ъ) при і =3.

Таким чином, кожний стовпець (2.34) є розподілом повідомлень Ь., спотвореним через статистичний вплив повідомлень а. є А [пор. із (2.31)]. Тепер, маючи дані (2.32), за (2.8) розрахуємо безумовну ентропію дже­рела А:

Я (А)= -(0,3 log 0,3 + 0,3 log 0,3 + 0,4 log 0,4)= = 1,57095 біт/повідомлення.

Аналогічно, маючи дані (2.31), за (2.28) обчислимо безумовну ентро­пію джерела В:

Я (В) = -(0,3 log 0,3 + 0,3 log 0,3 + 0,4 log 0,4) = = 1,57095 біт/повідомлення.

У розглядуваному прикладі Я (В) = Н (А) тому, що збігаються розпо­діли безумовних імовірностей. До речі, максимального значення Я (А) та И (В) досягли б при рівноймовірному розподілі ймовірностей, тобто при р (а) = 1/3 та/? (/?.) = 1/3 для і J є {1, 2, 3}.

Тоді було б

"шах И) = "_max (*) = -lOg (1/*) = lOg к = log 3 =

= 1,58496 біт/повідомлення.

Як бачимо, максимальна ентропія перевищує значення безумовної ентропії при нерівномірному розподілі ймовірностей.

Часткова умовна ентропія джерела А за (2.17) з урахуванням (2.33) становитиме

Я {АІЬ_Х) = -[(2/3) log (2/3) + 0 log 0 + (1/3) log (1/3)] = 0,91829 біт/повідомлення;

42

43

H (A/b₂) = -[0 log 0 + (2/3) log (2/3) + (1/3) log (1/3)] = = 0,91829 біт/повідомлення;

H (A/b₂) = -(0,25 log 0,25 + 0,25 log 0,25 + 0,5 log 0,5) =

= 1,5 біт/повідомлення.

Загальна умовна ентропія джерела А відносно джерела В згідно з (2.19) або (2.21)

Н (А/В) = 0,3 Н (Afb_x) + *0,3 Я (А/Ь₂) + 0,4 Я (А1Ъ_Ъ) = = 2-0,3 0,91829 + 0,4 ■ 1,5 = 1,15097 біт/повідомлення.

Часткова умовна ентропія джерела В за (2.18) з урахуванням (2.34) становитиме

Я (В/е,) = -[(2/3) log (2/3) + 0 log 0 + (1/3) log (1/3)] =

= 0,91829 біт/повідомлення;

Я (В/а₂) = -[0 log 0 + (2/3) log (2/3) + (1/3) log (1/3)] =

= 0,91829 біт/повідомлення;

Я\ВІа_г) = -(0,25 log 0,25 + 0,25 log 0,25 + 0,5 log 0,5) =

= 1,5 біт/ повідомлення.

Загальна умовна ентропія джерела В відносно джерела А згідно з (2.20) або (2.22)

Н\ВІА) = 0,3 • 2 • 0,91829 + 0,4 • 1,5 = 1,15097 біт/повідомлення.

Відзначимо окремо такі властивості умовної ентропії:

1. Якщо джерела повідомлень Атз.В статистично незалежні, то умовна ентропія джерела А відносно джерела В дорівнює безумовній ентропії джерела А й навпаки:

Н(А/В) = Н(А);Н(В/А) = Н(В).

2. Якщо джерела повідомлень А та. В настільки статистично взаємозв'язані, що виникнення одного з повідомлень спричи­ нює безумовну появу іншого, то умовні ентропії їх дорівнюють нулю:

Н(А/В) = Н(В/А) = 0.

3. Ентропія джерела взаємозалежних повідомлень (умовна ентропія) менша від ентропії джерела незалежних повідомлень (безумовна ентропія).

4. Максимальну ентропію мають джерела взаємонезалежних рівноимовірних повідомлень, умовна ентропія яких дорівнює нулю, а ймовірність появи символів алфавіту р = \/к, де к — кількість повідомлень в алфавіті.