1.4. Предмет теорії інформації та кодування

Теорія інформації— це розділ кібернетики, в якому за допо­могою математичних методів вивчаються способи вимірювання кількості інформації, що міститься в будь-яких повідомленнях, способи кодування для економічного подання повідомлень і на­дійної передачі їх по каналах зв'язку з завадами.

Курс теорії інформації об'єднує такі теоретичні напрями, як кількісна оцінка інформації, кодування повідомлень, їх стис­нення, оцінка ефективності та завадостійкості передачі кодо­ваних повідомлень.

Одним з головних завдань теорії інформації є максимальне використання потенційних можливостей каналів зв'язку на ос­нові оптимального кодування джерела повідомлення та його дальшого завадостійкого кодування. Це збігається з завданням теорії кодування — здобуттям ефективних алгоритмів кодуван­ня для джерел повідомлень і передачі даних по каналах зв'язку.

18

19

Теорія інформації та кодування за своєю природою дуже близька до математичних дисциплін; тому як апарат досліджен­ня в ній застосовуються теорія скінченних полів, лінійна алгеб­ра, комбінаторика, теорія матриць, теорія ймовірностей та ма­тематична статистика.

Без розвитку теорії інформації та кодування і впровадження її в життя практично неможливо створення складних систем керування супутниками Землі та ракетами, систем і мереж зв'яз­ку та передачі даних, складних ЕОМ і комплексів тощо.

Засвоєння матеріалу курсу теорії інформації та кодування є не­обхідним для дальшого оволодіння знаннями в галузі збирання, передавання, перетворення, оброблення, накопичення та зберігання інформації, проектування та розроблення інформаційних систем і засобів автоматики та інформатики будь-якого призначення.

Інтерес до теорії інформації та кодування, а також до техніч­них засобів реалізації її положень зростатиме зі збільшенням об­сягів потоків обміну інформацією. Ця тенденція прослідковуєть-ся в усіх галузях науки та техніки. Провадиться багато досліджень щодо розробки нових класів кодів, способів захисту інформації від несанкціонованих втручань у потоки інформації, вдоскона­лення способів і засобів її кодування та декодування.

КОНТРОЛЬНІ ЗАПИТАННЯ

1. Що таке повідомлення?

2. У чому полягає різниця між даними, повідомленнями та інформацією?

3. Що таке сигнал?

4. Які бувають сигнали?

5. Якими параметрами характеризуються сигнали?

6. Як узгодити ємність каналу та обсяг сигналу?

7. Чим характеризуються неперервні та дискретні повідомлення?

8. Які основні вузли систем передачі інформації та яке призначення їх?

9. Що таке лінія та канал зв'язку?

10. У чому полягає різниця між лінією та каналом зв'язку?

11. У чому полягають операції перетворення сигналу на повідомлення при передачі інформації?

12. Які відмінності багатоканальної системи передачі інформації від одноканальної?

13. Які бувають математичні моделі каналів зв'язку?

14. Що таке ідеальний канал зв'язку без завад?

15. У чому полягає особливість каналу зв'язку з адитивним гауссовим шумом?

16. Яка різниця між одно- та багатопроменевим каналами зв'язку?

17. Які особливості каналу зв'язку з невизначеною фазою сигналу?

18. Які відмінності між симетричним і несиметричним каналами зв'язку?

19. Що таке симетричний канал зв'язку без пам'яті?

20. Які математичні моделі дискретних каналів зв'язку застосовуються при моделюванні реальних каналів?

21. Що вивчається в дисципліні «Теорія інформації та кодування»?

КІЛЬКІСНІ

ХАРАКТЕРИСТИКИ

ІНФОРМАЦІЇ

РОЗДІЛ

Обговорюючи кількісні характеристики будь-якого досліджуваного об'єкта, мають на увазі насамперед можливість і вміння вимірювати ту чи іншу характеристику. Ця можливість визначається доступнії* тю об'єкта та наявністю вимірювального пристрою, а вміння нанп* ністю та знанням кількісної міри і процедур чи методик її шетосуттн*

Звісно, вибір міри є актом довільним. Можна вибрати тгачьно-прийняту міру, скажімо, метр для вимірювання довжини деякого об «•*• та. А можна вибрати й щось інше, як у відомому мультиплікаційному фільмі, де герої вимірювали довжину удава в папугах, діставши J ft minyi.

У теорії інформації поряд з іншими вирішуються питання вимірні вання кількості інформації. При цьому потребують свого виточений об 'єкти дослідження — джерела повідомлень і моделі їх, ижре \т tmvtiM* блі повідомлень. Нижче описуються особливості джерел повідомлень, дається оцінка кількості інформації в повідомленнях, наводяться шли* стивості ентропії та її різновиди.

2.1. АНСАМБЛІ ТА ДЖЕРЕЛА ПОВІДОМЛЕНЬ

Матеріальному світові, що оточує людину, притаманна без­ліч фізичних явищ, багато з яких змінюються в часі, маючи форму фізичних процесів, тобто таких явищ, фізичні показни­ки яких не є миттєвими, а розподіленими в часі, які можна спо­стерігати кожної миті.

Будь-який матеріальний об'єкт разом із спостерігачем у і їм» рює систему, яка називається джерелом повідомлень [15,44]. 11.1 рис. 2.1 зображено схему системи взаємозв'язаних об'єктін і спостерігачів, вкладених одне в одне, стосовно передачі відо­мостей про певний фізичний об'єкт певному одержувачеві. Дим кожної стрілки на рис. 2.1 частина системи, розміщена ліворуч, може розглядатися, як спостережуваний об'єкт, а розташова­на праворуч — як спостерігач. При цьому не має значення ііри-рода спостерігача: чи це людина, чи це якийсь прилад. Його головне завдання полягає в перетворенні відомостей про стан

21

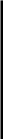
а_ьа₂ а_к

Канал, або спостерігач В

а,єА

-1

	Об'єкт	Фізичний процес		Слотерігач А
				Джерело А і

b,,b₂,...,b_n

Джерело В

Одержувач С (спостерігач С)

Ь&В

Джерело С

CjEC

Спостерігач

Рис. 2.1

спостережуваного об'єкта на форму, зручну для прийняття ін­шими людиною або приладом.

Стан матеріального об'єкта, а отже, і його фізичні показни­ки можуть набувати значення з певного дискретного набору значень. Джерело повідомлень з таким об'єктом є дискретним. Якщо стан матеріального об'єкта, відбитий у його фізичних показниках, набуває значення з нескінченної множини можли­вих значень, то таке джерело повідомлень є неперервним. Прин­ципово воно може бути зведене до дискретного, якщо прийняти допустимий рівень похибки та за її допомогою з нескінченної множини можливих значень повідомлень вибрати певний дискретний набір. Саме тут у наявності похибки та її допусти­мому рівні криється принципова різниця між дискретним і не­перервним джерелами повідомлень. Докладніше це питання роз­глядається в розд. 4.

Якщо під час деякого часового проміжку дискретним дже­релом вибрано деяке повідомлення я_/5 яке ніяк не зумовлене повідомленням а_м, вибраним у попередній проміжок часу, то таке джерело є дискретним джерелом без пам 'яті.

Якщо в деякому часовому проміжку дискретним джерелом вибрано повідомлення а₀ пов'язане з попереднім повідомлен­ням д_м і статистично зумовлене ним, то таке джерело назива­ється дискретним джерелом із пам'яттю.

Крім дискретних, можуть бути також неперервні джерела повідомлень із пам яттю та без пам 'яті (див. п. 4.4). Перелічени­ми тут типами не вичерпуються всі відомі джерела повідомлень. Специфічні джерела повідомлень, в яких враховано статистич­ні якості фізичних параметрів, розглядаються в [3, 35, 44].

Якщо кожного проміжку часу дискретне джерело повідом­лень вибирає одне з k можливих повідомлень a_v я₂, ...,%, то кажуть, що А = {а_{9 ..., а_к} є дискретною множиною повідом­лень, або просто множиною повідомлень А. Як правило, для повнішого опису джерела повідомлень на множині А визнача­ють її ймовірнісну міру, тобто з кожним дискретним повідом­ленням а_і пов'язують ймовірність р. його вибору джерелом. Таким чином, множині А-{а_х,..., а_к} зіставляється ймовірнісна міра у вигляді множини Р_к = {p_v ...,р_к}, на яку накладено обме-

к ження у вигляді YjPi ~ 1 • 1=1

Дві множини А та Р дають достатньо повний опис дискрет­ного джерела повідомлень у вигляді його ймовірнісної моделі, а тому разом вони утворюють ансамбль повідомлень дискрет­ного джерела. Це означає, що кожного проміжку часу дискрет­ним джерелом вибирається певне повідомлення а_х є А з імовір­ністю p(a_t) = p_t є P. Наведене вище обмеження є природною умовою включення до складу множини А повної групи подій, якими виступають дискретні повідомлення. Ця вимога з'явля­ється тут тому, що надалі треба скористатися апаратом мате­матичної статистики, звідки й походить цей термін. Це дає змогу врахувати при розгляді всі обговорювані події-повідомлення. За своїм розсудом можна змінити склад можливих повідомлень в А, але слід пронормувати їх ймовірності так, щоб сума ймовір­ностей дорівнювала одиниці.