3. Потенциальное поле вида

Р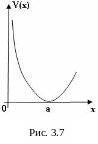 ассмотрим одномерное движение в потенциальном поле вида

(3.3.1)

(см. рис.3.7). Стационарное уравнение Шредингера при этом имеет вид

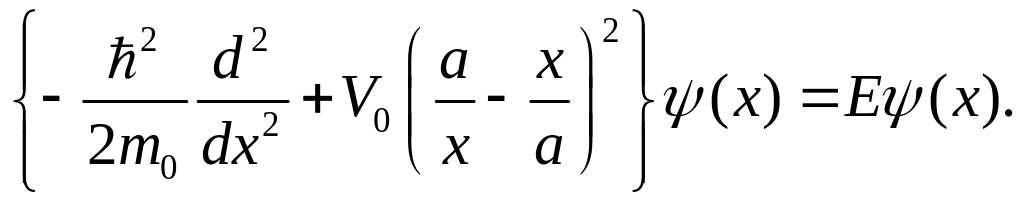(3.3.2)

Рассмотрим асимптотическое поведение функции при больших значениях аргумента . Тогда вместо уравнения (3.3.2), оставляя лишь существенные для больших величины, имеем

(3.3.3)

Перейдем к новой переменной :

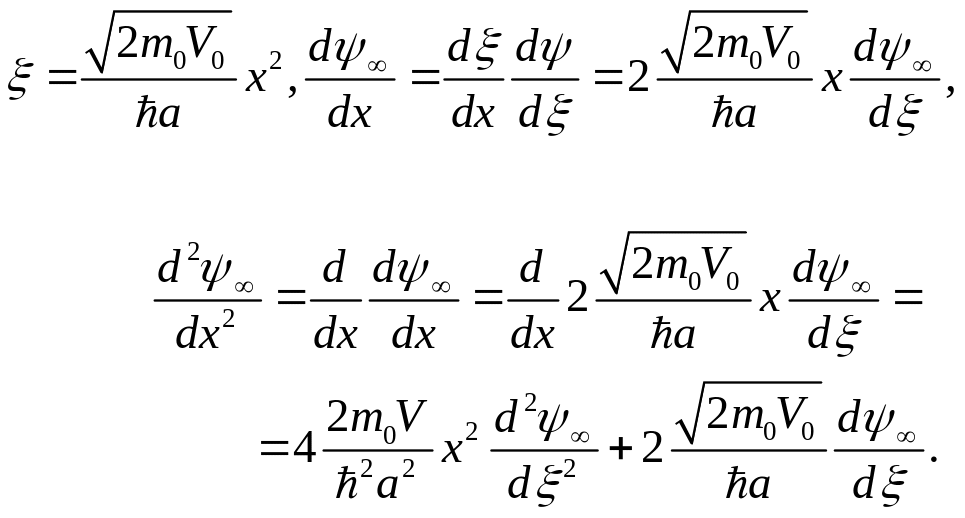(3.3.4)

Учитывая это, а также, что соответствует , вместо (3.3.3) получаем

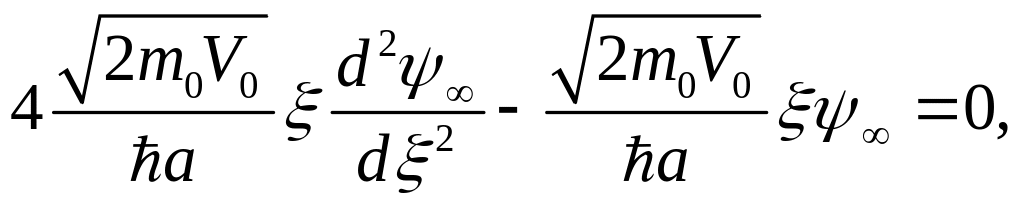(3.3.5)

или

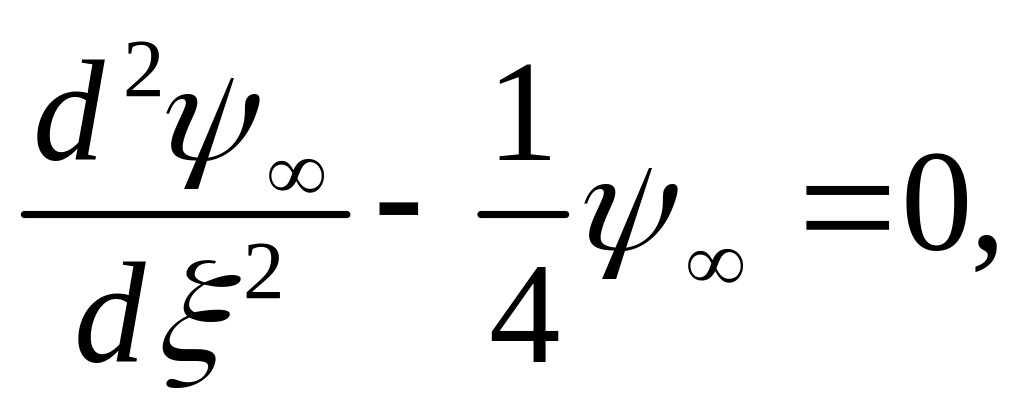(3.3.6)

откуда для общего решения дифференциального уравнения можно записать

(3.3.7)

Из требования ограниченности волновой функции необходимо положить C₂ = 0. Поскольку волновая функция еще не нормирована, полагаем C₁ = 1, т.е.

(3.3.8)

Для определения поведения волновой функции в нуле от уравнения (3.3.2) переходим к уравнению

(3.3.9)

или в переменных , согласно (3.3.4),

(3.3.10)

Ищем функцию в виде

(3.3.11)

Подставляя частное решение (3.3.11) в уравнение (3.3.12), получаем

(3.3.12)

откуда

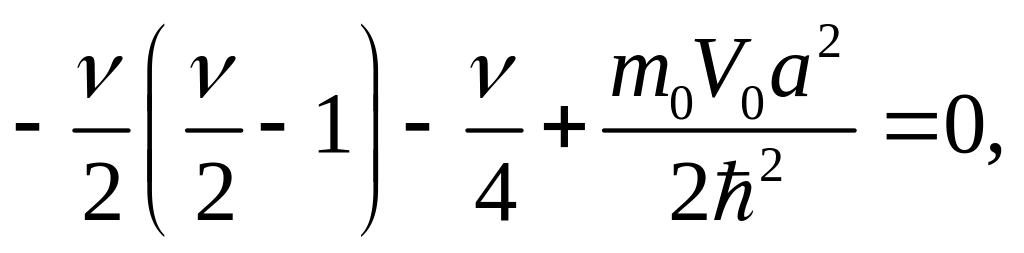(3.3.13)

или

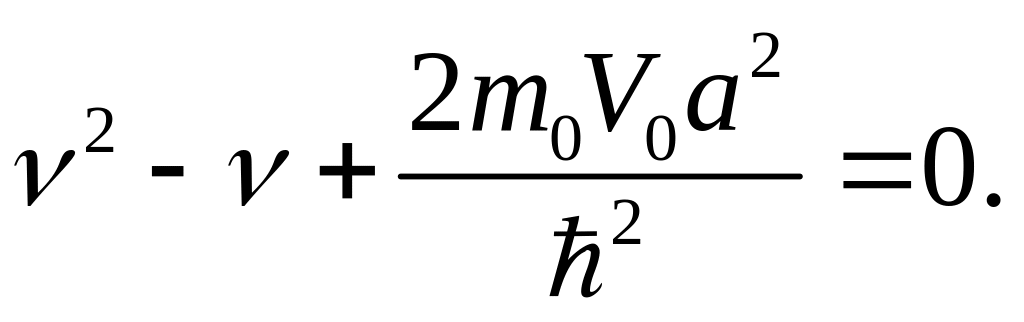(3.3.14)

Корни этого уравнения

(3.3.15)

Из соображений ограниченности волновой функции в нуле принимаем

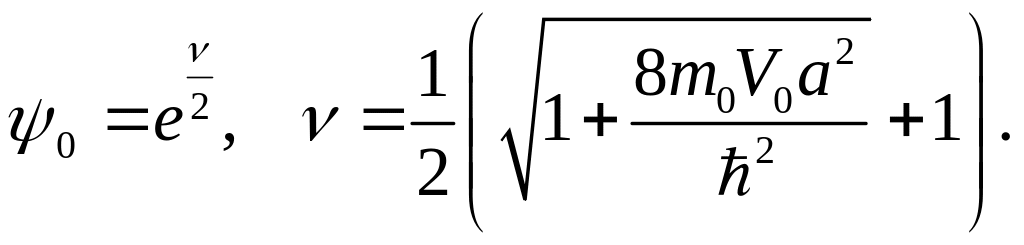(3.3.16)

Учитывая сведения о поведении волновой функции в нуле и на бесконечности (см. функции (3.3.8) и (3.3.16)), ищем волновую функцию в виде

(3.3.17)

Из (3.3.17) следует, что

(3.3.18 a)

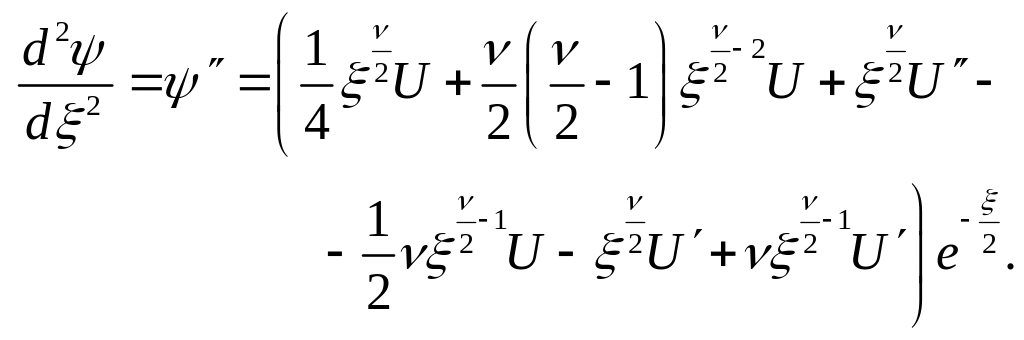(3.3.18 b)

Подставляя (3.3.17), (3.3.18) с учетом (3.3.4) в (3.3.2), после сокращения на экспоненту получаем следующее уравнение :

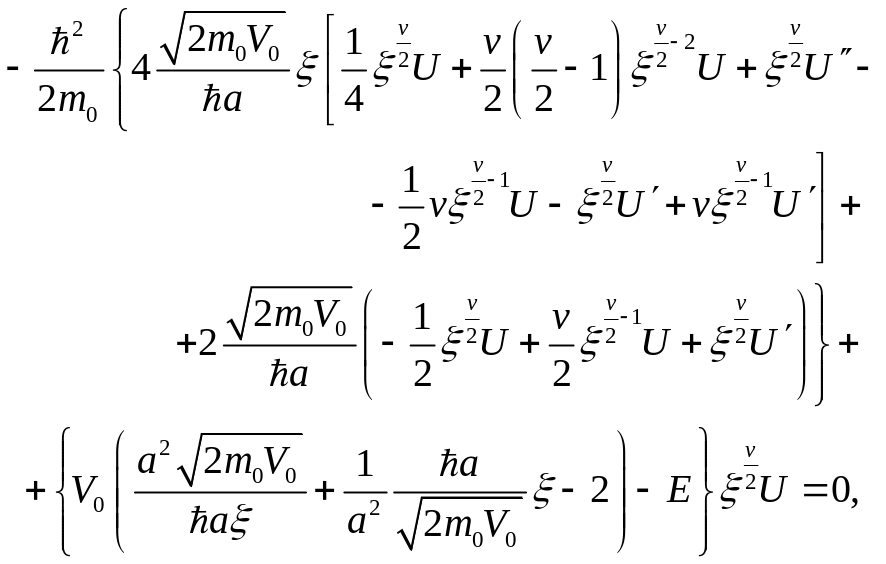(3.3.19)

откуда после перегруппировки членов и сокращения на и постоянный множитель при старшей производной, имеем

(3.3.20)

Поскольку выделенные слагаемые в соответствии с (3.3.13) взаимно компенсируются, получаем окончательно следующее уравнение для неизвестной функции :

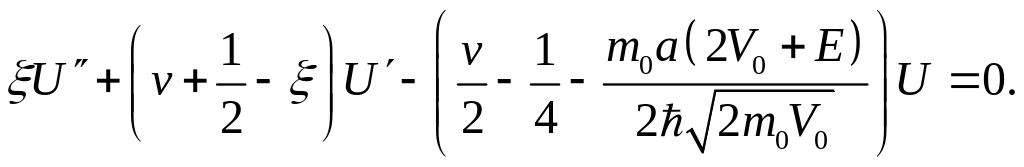(3.3.21)

Уравнение (3.3.21) представляет собой уравнение для вырожденной гипергеометрической функции. Стандартная форма последнего имеет вид

(3.3.22)

Общее решение этого уравнения есть суперпозиция

(3.3.24)

где

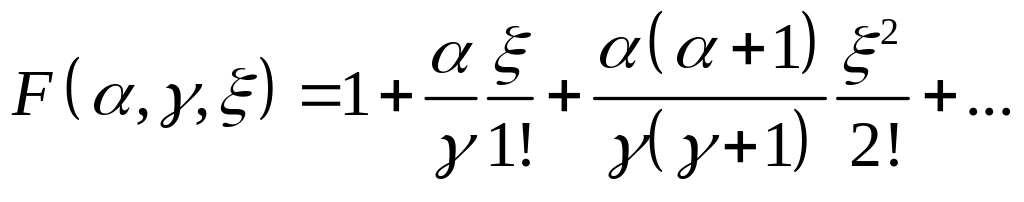(3.3.24)

Очевидно, что для ограниченности волновой функции необходимо потребовать Второе слагаемое в (3.3.23) имеет особую точку при .

Сравнивая уравнения (3.3.21) и (3.3.22), для искомой функции можно записать

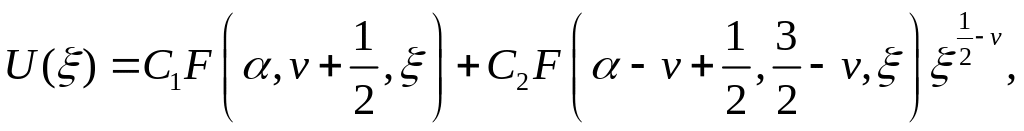(3.3.25)

где

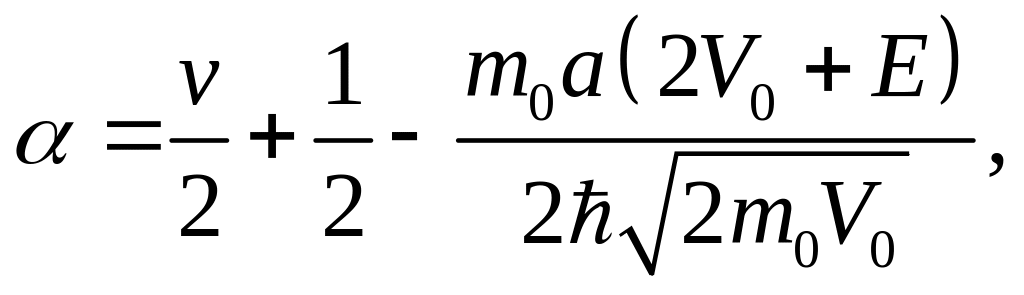(3.3.26)

поскольку , из требования ограниченности волновой функции в

нуле C₂ = 0. Кроме того, в соответствии с асимптотикой функции , необходимо потребовать, чтобы волновая функция при убывала, т.е. чтобы функция сводилась к полиномам. Этого можно добиться, полагая

(3.3.27)

откуда приходим к квантованию энергетических уровней

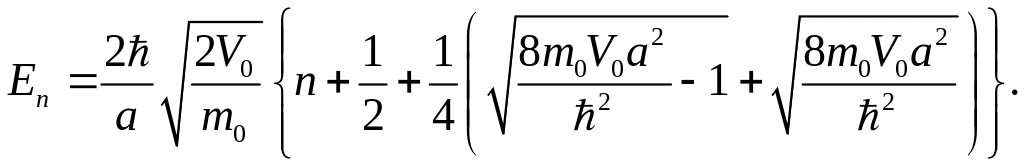(3.3.28)

Таким образом, энергетический спектр, с точностью до выбора начала отсчета энергии, оказывается таким же, как у гармонического осциллятора с циклической частотой 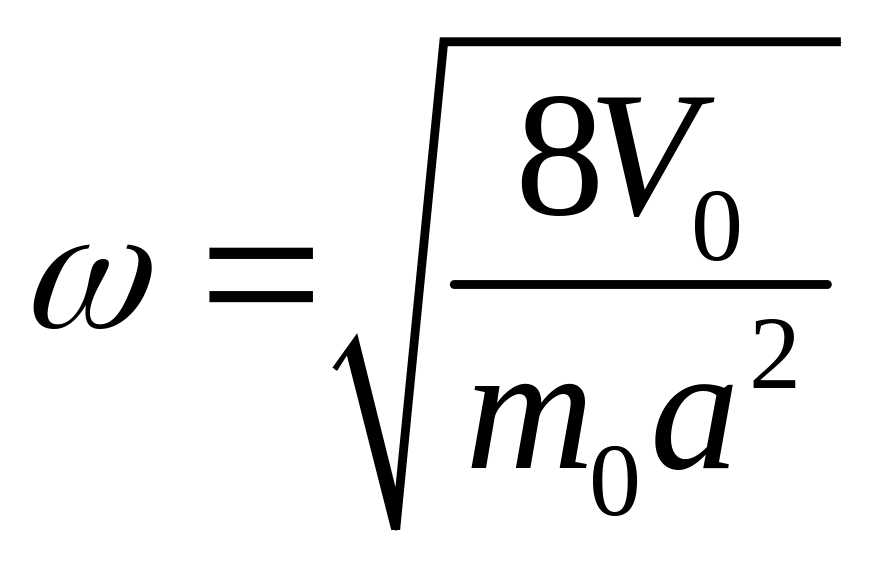. При этом нулевая энергия микрочастицы в поле 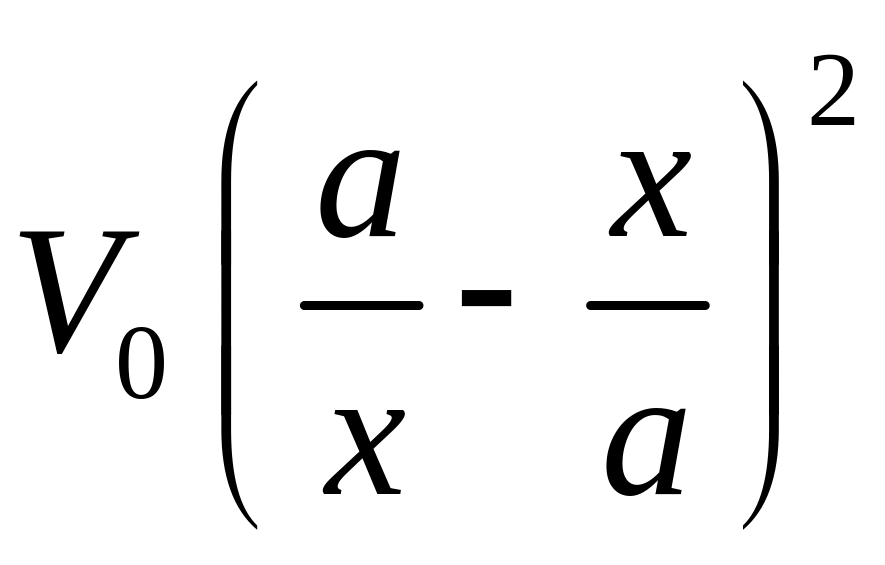всегда превышает энергию соответствующего осциллятора.

Для волновой функции частицы в рассматриваемом поле, согласно (3.3.17), имеем

(3.3.29)

где ν определено формулой (3.3.16), а константа может быть найдена из условия нормировки.