Глава 3. Движение микрочастиц в поле потенциальных сил

3.1 Частица в поле потенциальной ямы

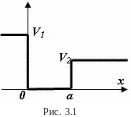
Р ассмотрим дозволенные значения энергии и волновые функции частицы с одной степенью свободы в потенциальном поле вида

(3.1.1)

Такое поле называют одномерной потенциальной ямой. В общем случае яма несимметрична, т.е. (см. рис. (3.1)).

Поскольку гамильтониан системы не зависит явно от времени

, (3.1.2)

задача сводится к изучению стационарных состояний, т.е. волновая функция имеет вид

(3.1.3)

а и определяются стационарным уравнением Шредингера

(3.1.4)

Запишем это уравнение для областей , , :

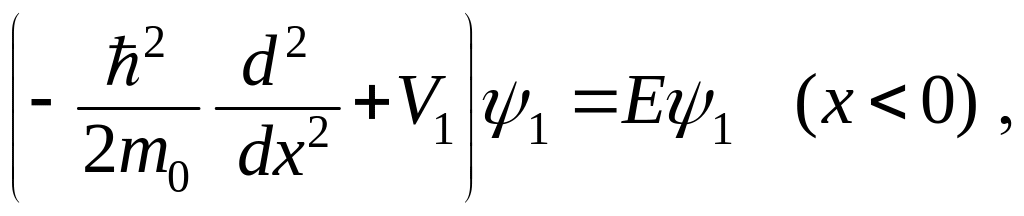(3.1.5a)

(3.1.5b)

(3.1.5c)

Поскольку речь идет о некоторых конкретных стационарных состояниях с определенными значениями , необходимо искать решение уравнений (3.1.5) при одном и том же значении , а , , рассматривать как части одной и той же волновой функции, определенное в соответствующих областях изменения .

Преобразуем уравнения (3.1.5):

(3.1.6a)

(3.1.6b)

(3.1.6c)

Вводя величины

(3.1.7)

вместо (3.1.6) имеем

(3.1.8)

Сначала рассмотрим связанные состояния, т.е. состояния, когда частица не уходит на бесконечность. В этом случае . Кроме того, в выбранной системе координат энергия частицы , поэтому и , , . Решения уравнений (3.1.8) очевидны

(3.1.9a)

(3.1.9b)

(3.1.9c)

Для того чтобы найти коэффициенты в уравнениях (3.1.9), необходимо вспомнить об условиях, накладываемых на волновую функцию. Она должна быть непрерывной и однозначной, что дает два условия при и при . Непрерывной и однозначной должна быть и первая производная волновой функции – это еще два условия. Требования ограниченности волновой функции в данном случае приводят еще к двум условиям при и при . Итого, шесть неизвестных коэффициентов и шесть условий (шесть уравнений). На первый взгляд, кажется, что определяются все коэффициенты (число уравнений равно числу неизвестных), что противоречит определению волновой функции. Последняя всегда определена с точностью до произвольного множителя, который впоследствии может быть использован для нормировки. Таким образом, если задача решена правильно, в нашем распоряжении всегда должен остаться произвольный коэффициент для нормировки, если эта нормировка не была принята где-либо в процессе решения. На примере данной задачи мы впоследствии в этом убедимся.

Итак, полагая, в силу требования конечности волновой функции, , , для оставшихся коэффициентов запишем явно условия

(3.1.10)

имеем

(3.1.11)

Перенося все величины в левую часть, получаем следующую систему уравнений:

(3.1.12)

(3.1.12) представляет собой однородную систему алгебраических уравнений относительно неизвестных , , , . Заметим, однако, что через величины , , здесь имеется еще одно неизвестное – энергия . Для того чтобы система (3.1.12) имела нетривиальные решения, необходимо потребовать обращения в нуль ее определителя:

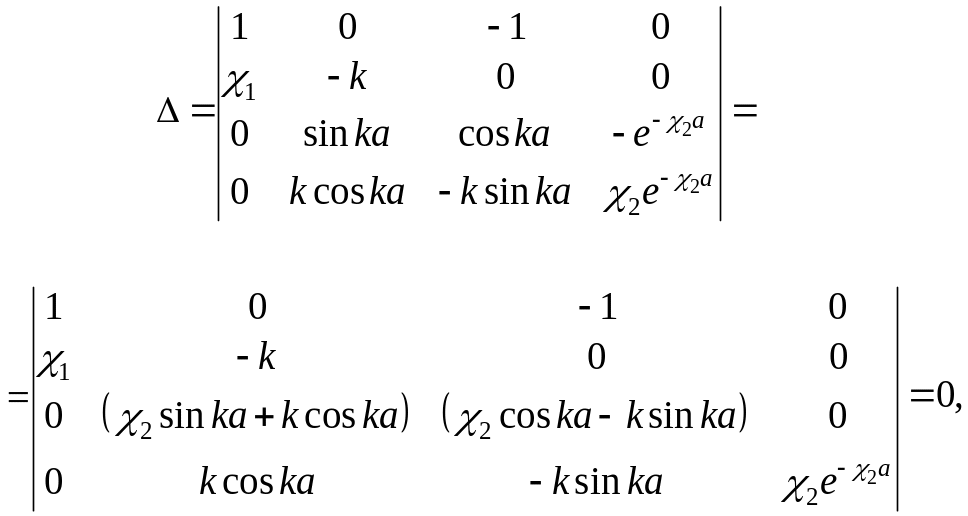(3.1.13)

откуда получаем

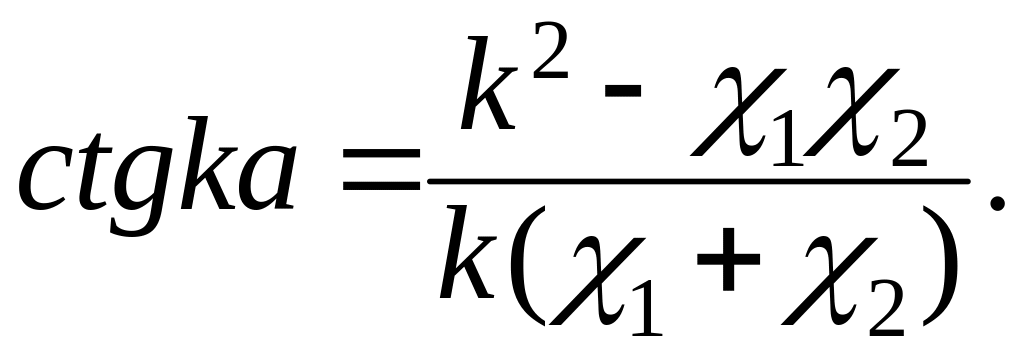(3.1.14)

Далее воспользуемся известной формулой тригонометрии

(3.1.15)

и тем фактом, что является периодической функцией с периодом . Получаем решение уравнения (3.1.14)

(3.1.16)

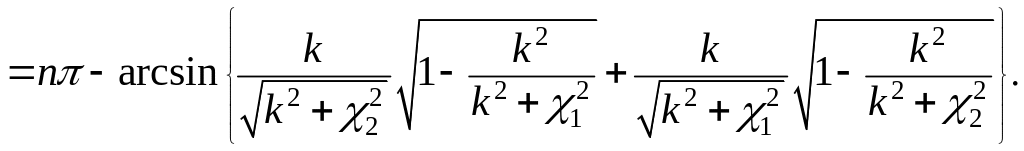
Далее воспользуемся соотношением

(3.1.17)

В результате, вспоминая определение параметров , , , получаем

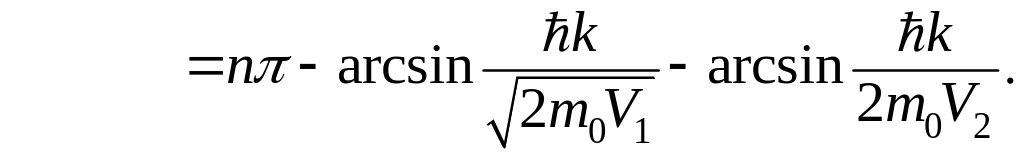(3.1.18)

В этом уравнении лишь одна неизвестная величина, подлежащая определению: это , связанная, в свою очередь, с энергией частицы, согласно (3.1.7),

(3.1.19)

Таким образом, решая трансцендентное уравнение (3.1.18), определяем дозволенные значения энергии для связанных состояний в потенциальной яме (3.1.1). Значения , удовлетворяющие уравнению (3.1.18), удобно находить графически. Эти значения лежат на пересечении прямой

(3.1.20)

и кривых

(3.1.21)

См. рис. 3.2. Естественно, что, ввиду финитности движения, энергия проквантовалась и ее значения можно пронумеровать

(3.1.22)

Для того чтобы найти соответствующие волновые функции, поступим следующим образом. Подставляем конкретные значения в систему однородных алгебраических уравнений (3.1.12). Поскольку найдены из требования (3.1.13), определитель системы уравнений (3.1.12) при этом равен нулю, и, следовательно, не все уравнения системы являются линейно независимыми; одно из них является следствием остальных. Таким образом, число уравнений оказывается на единицу меньше, чем число определяемых неизвестных констант. Поэтому одну из постоянных можно задать произвольно, например, , а остальные выразить через нее. впоследствии можно использовать для нормировки функции. Как и предполагалось выше, одна из констант оказалась в нашем распоряжении (для нормировки), так как волновая функция определена с точностью до произвольного постоянного множителя. Нормировка функции не меняет физического содержания, позволяя лишь работать в привычных категориях теории вероятностей.

О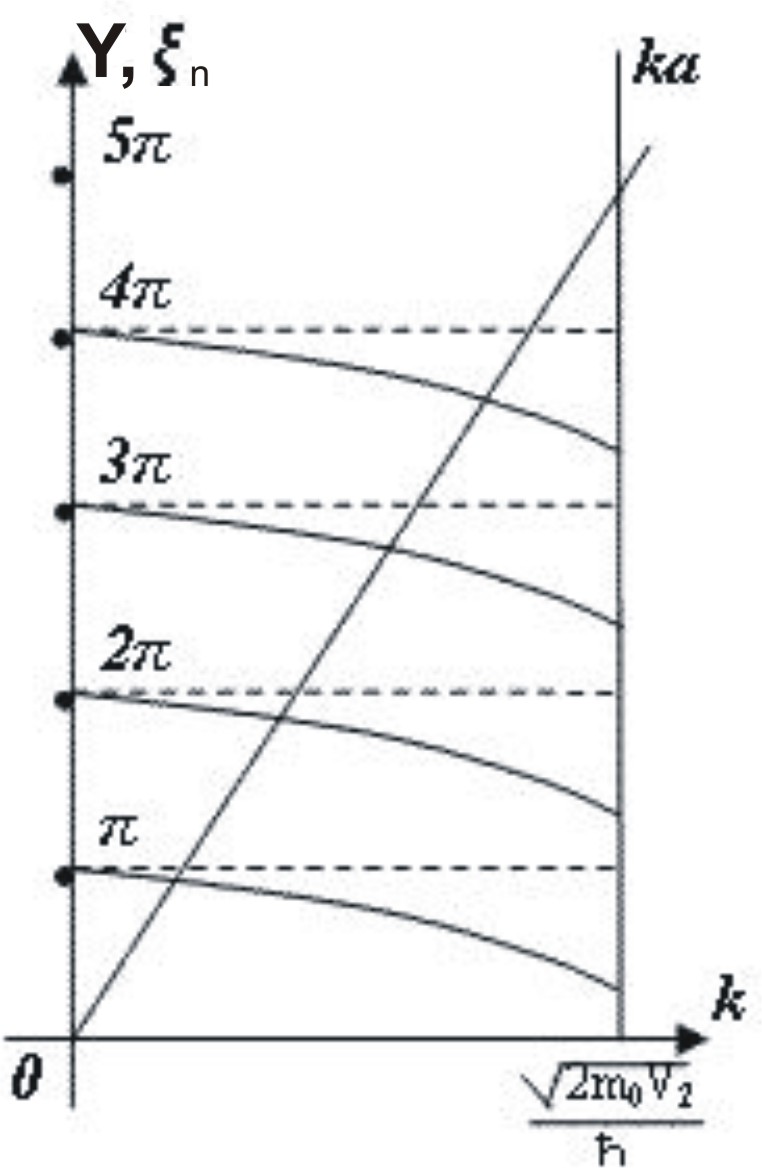 бращаясь к системе уравнений (3.1.12), можем положить, например,

(3.1.23)

Волновые функции, соответствующие конкретным значениям , а следовательно и , , имеют вид

(3.1.24)

Нетрудно убедиться в выполнении первых трех граничных условий (3.1.11). В выполнении последнего из условий (3.1.11) можно убедиться лишь при конкретном значении из уравнения (3.1.18), что может быть сделано (ввиду трансцендентности этого уравнения) лишь численно.

В общем случае лишь численно можно провести и нормировку волновой функции (3.1.24) на единицу. Соответствующее условие нормировки можно записать следующим образом:

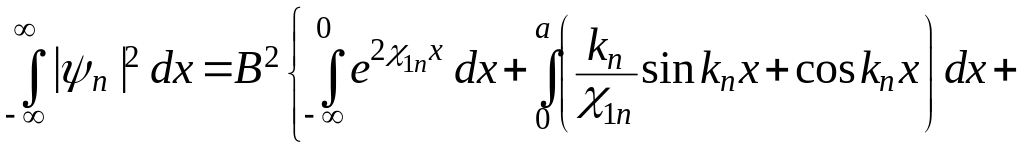
(3.1.25)

Уместно указать на важнейший факт квантовой механики, а именно – оказывается, что в случае квантовой механики возможно движение в областях, где классическое движение невозможно. В самом деле, при и энергия микрочастицы . Тем не менее, , в этих областях, т.е. отлична от нуля вероятность пребывания частицы в этих областях. Другое дело, что вероятность обнаружить частицу при и экспоненциально спадает по мере продвижения частицы вглубь области, где движение классически не дозволенно. Однако сам факт возможности движения в классически запрещенных областях имеет принципиальное значение.

Р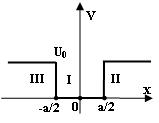 ассмотрим теперь симметричную потенциальную яму. В этом случае удобно выбрать координаты несколько иным образом, нежели это сделано для несимметричной ямы (см. рис. 3.1 и рис. 3.3). Итак, потенциальное поле, в соответствии с рис. 3.3, имеет вид

(3.1.26)

Поскольку гамильтониан системы в этом случае коммутирует с оператором пространственной инверсии, или, что то же самое

(3.1.27)

стационарные состояния в этом случае будут обладать определенной четностью. При положительной четности

(3.1.28)

а при отрицательной четности

(3.1.29)

В связи с этим достаточно найти решения лишь для положительных (или отрицательных) значений . Волновые функции состояний с отрицательной четностью, в соответствии с (3.1.29), обращаются в нуль при , а для волновой функции состояний с положительной четностью при в нуль обращаются соответствующие первые производные.

Как и в предыдущем случае, рассматривая связанные состояния, т.е. микрочастицы, обладающие энергией , запишем уравнение Шредингера соответственно для областей I и II :

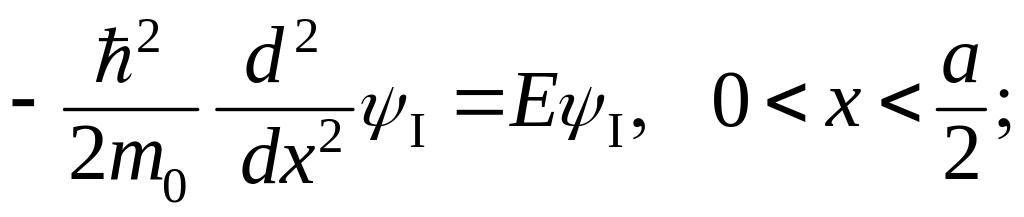
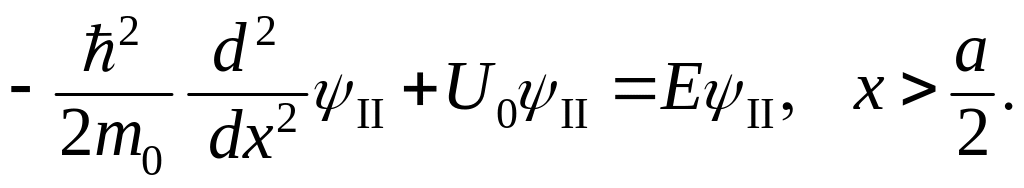(3.1.30)

Отсюда, вводя следующие обозначения :

(3.1.31)

получим

(3.1.32)

Решения этих уравнений имеют следующий вид:

(3.1.33)

где знаки , отмечают четность состояний;

(3.1.34)

Из соображений конечности волновой функции при необходимо положить .

Итак, в случае положительной четности волновая функция задается выражением

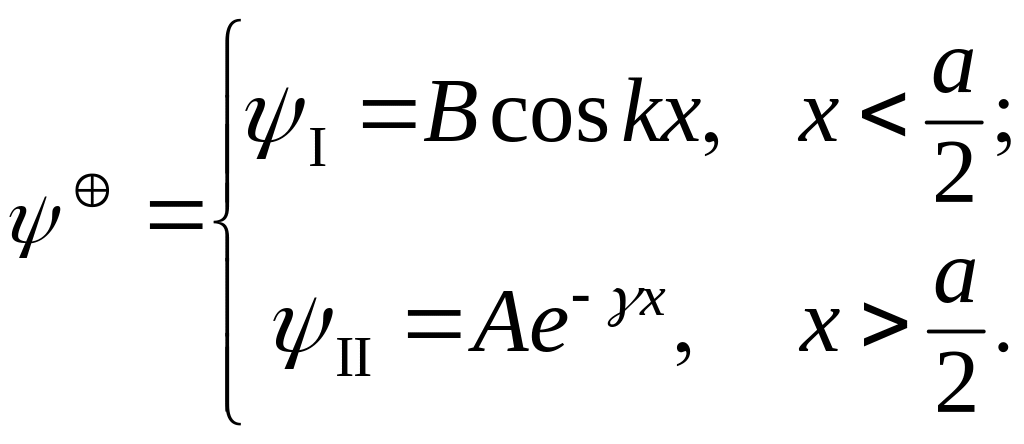(3.1.35)

Требуя непрерывности функции и ее производной при , получаем

(3.1.36)

или

(3.1.37)

Потребуем далее, чтобы волновая функция не обращалась тождественно в нуль, т.е. интересуемся нетривиальными решениями. Для этого необходимо, чтобы определитель однородной системы алгебраических уравнений (3.1.37) относительно неизвестных и равнялся нулю

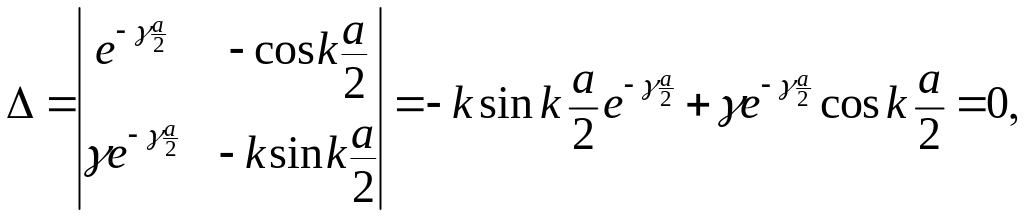(3.1.38)

откуда

(3.1.39)

Учитывая, что периодичность равна , имеем

(3.1.40)

Воспользовавшись известной формулой из тригонометрии

вместо уравнения (3.1.40) получаем

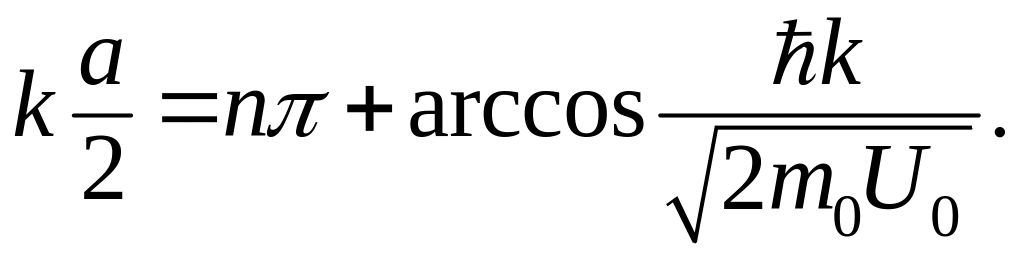(3.1.41)

Значения , удовлетворяющие этому уравнению, можно найти графически на пересечении прямой и кривых

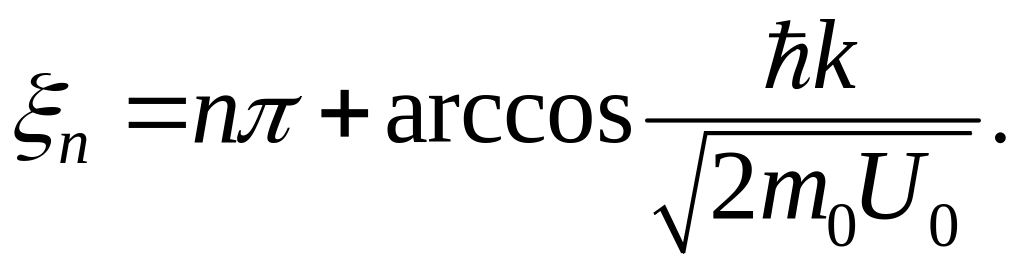(3.1.42)

Поскольку аргумент арккосинуса не может превышать единицы, то значения лежат в интервале

(3.1.43)

Подставляя конкретное значение в уравнение (3.1.37), получим фактически лишь одно уравнение для двух неизвестных постоянных и , так как найдено из условия обращения в нуль определителя этой системы уравнений. Выбирая одну из них произвольно (впоследствии ее можно определить из условия нормировки), приходим к следующему решению задачи для состояний с положительной четностью:

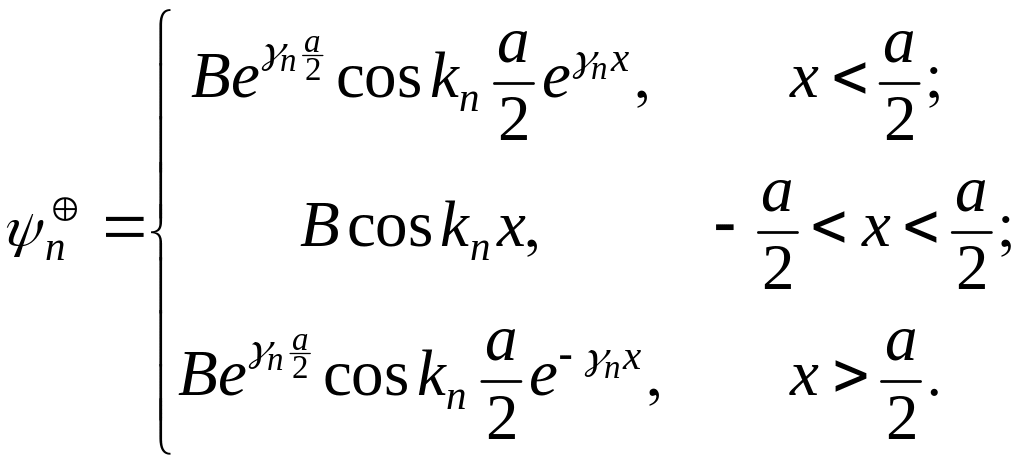(3.1.44)

Условие нормировки этой волновой функции имеет вид

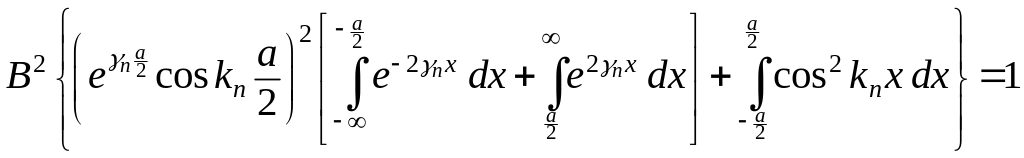(3.1.45)

Наконец, для энергетических состояний имеем, как и в предыдущей задаче, выражение (3.1.22).

В случае нечетных решений (3.1.33) можно записать граничные условия вида

(3.1.46)

или, переписывая их в виде однородной системе алгебраических уравнений относительно неизвестных и , получаем

(3.1.47)

откуда в качестве условия существования нетривиальных решений требуем

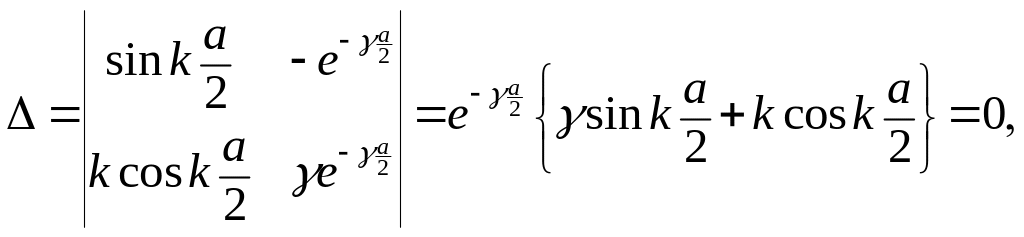(3.1.48)

или

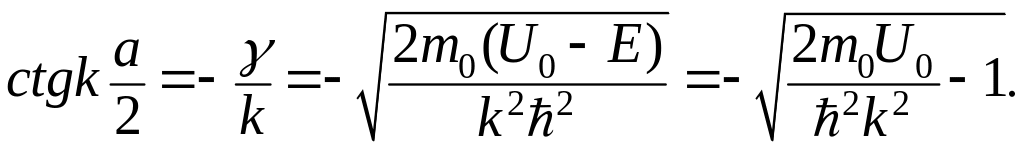(3.1.49)

Используя формулу (3.1.15), получаем

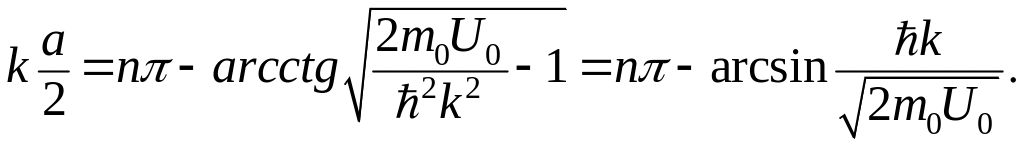(3.1.50)

Условие, которому должен удовлетворять аргумент арксинуса, снова требует выполнения соотношения (3.1.43). Значения , удовлетворяющие уравнению (3.1.50), определяются графически на пересечении функций

(3.1.51)

Для конкретных , возвращаясь к (3.1.46), имеем следующие волновые функции отрицательно четных состояний

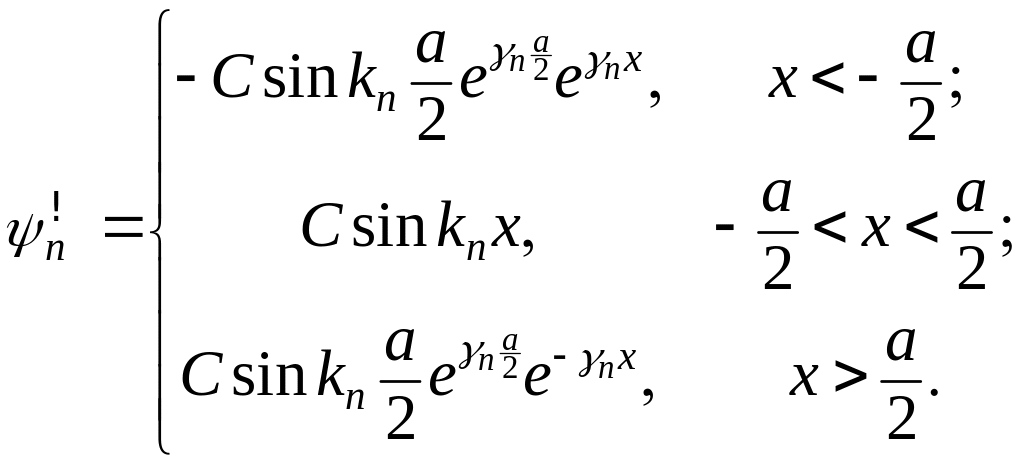(3.1.52)

Условие нормировки запишем в виде

(3.1.53)

Значения энергии снова определяются выражением (3.1.19). Итак, дискретные энергетические уровни в симметричной потенциальной яме определяются точками пересечения прямой и монотонно убывающих кривых . Поскольку возрастает, а монотонно убывает, то условие их пересечения имеет вид

(3.1.54)

или

(3.1.55)

Это условие всегда выполняется при . Поэтому в симметричной потенциальной яме при любых и имеется всегда не менее одного дискретного уровня. Возможное число дискретных уровней в симметричной яме определяется максимальным , при котором выполняется это условие

(3.1.56)

Рассмотрим далее бесконечно глубокую потенциальную яму, когда потенциальная энергия имеет вид

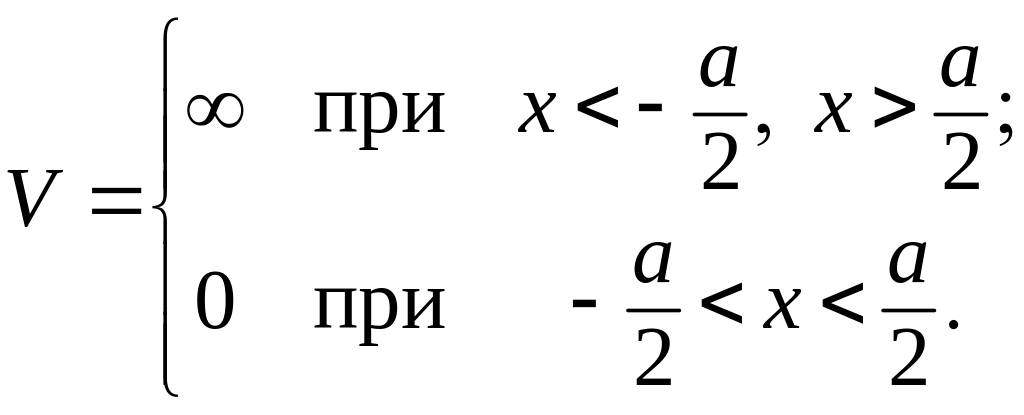(3.1.57)

(см. также рис. 3.4). При этом удобно воспользоваться результатами, полученными для симметричной потенциальной ямы конечной глубины.

В место выражений (3.1.31) теперь получаем

(3.1.58)

В связи с этим волновая функция в областях II и III тождественно равна нулю.

Тождественным нулем будет и ток вероятности в этих областях. Итак,

(3.1.59)

Однако волновая функция и ее производная в области I отличны от нуля, т.е. отличны от нуля плотность вероятности и плотность тока вероятности. Таким образом, невозможно одновременно удовлетворить требованиям, накладываемым на волновую функцию в точках , а именно требованиям непрерывности волновой функции (непрерывности плотности вероятности) и непрерывности производной волновой функции (непрерывности плотности тока вероятности). Это связано с излишней идеализацией задачи – ее неестественностью. (В природе нет бесконечно глубоких ям вида (3.1.57)). Поэтому необходимо остановиться лишь на одном из граничных условий. Находясь в области I, частица с отличной от нуля веротностью может подходить к стенкам ямы при , т.е. плотность тока вероятности в точках в области I отлична от нуля. Но частица не проникает в области II и III, и поэтому плотность тока вероятности в точках претерпевает разрыв. Условие непрерывности волновой функции в точках может и должно быть выполнено.

Обращаясь к состояниям с положительной четностью, имеем в соответствии с (3.1.35)

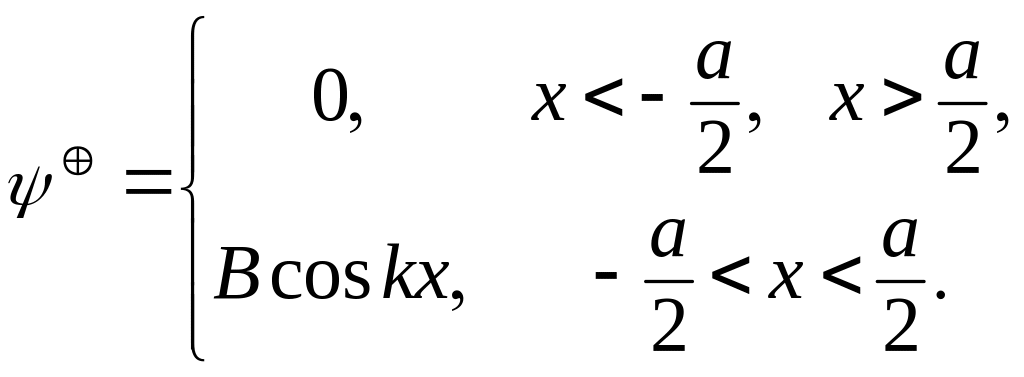(3.1.60)

Из граничных условий при получим

(3.1.61)

откуда

(3.1.62)

Итак, движение финитно, и для можно теперь записать

(3.1.63)

Из условия нормировки получаем

(3.1.64)

откуда

(3.1.65)

Соответствующие значения энергии определяются выражением

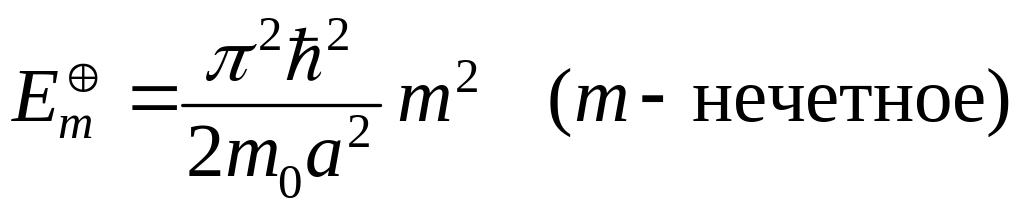. (3.1.66)

Для состояний с отрицательной четностью можно соответственно записать

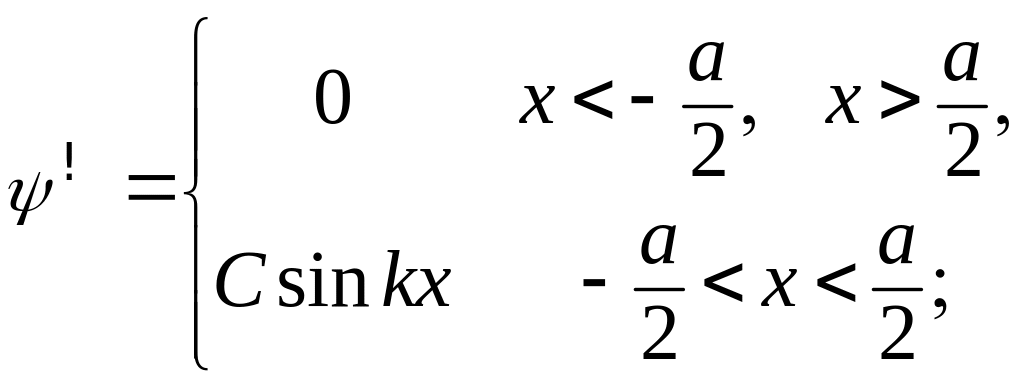(3.1.67)

(3.1.68)

(3.1.69)

(3.1.70)

(3.1.71)

(3.1.72)

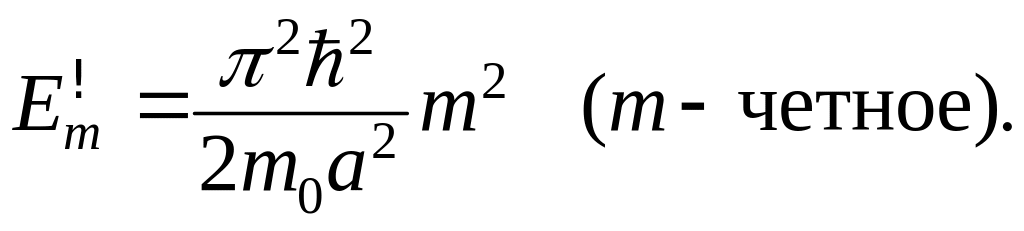(3.1.73)

К результатам, представленным формулами (3.1.65), (3.1.66), (3.1.72) и (3.1.73), можно прийти также, воспользовавшись данными, полученными для случая несимметричной потенциальной ямы. Для этого необходимо в выражении (3.1.1) и далее перейти к пределу , .

Тогда из (3.1.8) следует

(3.1.74)

Вместо волновой функции (3.1.9) имеем

(3.1.75)

Из (3.1.18) получаем условие квантования энергии

(3.1.76)

откуда

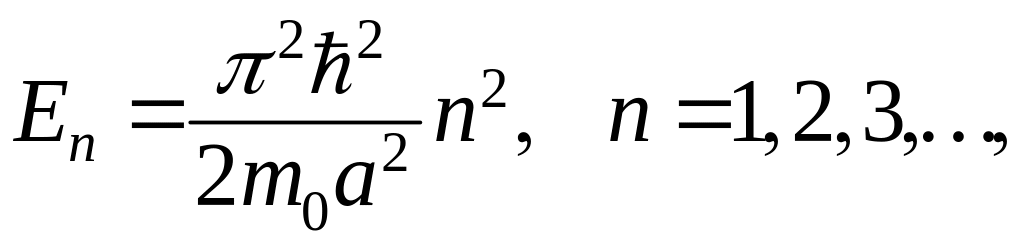(3.1.77)

что совпадает с совокупностью значений (3.1.66) и (3.1.73).

Используя формулы (3.1.24), для волновой функции получаем

(3.1.78)

что с учетом различия использованных координат (рис. 3.1 и рис. 3.3) соответствует множеству функций (3.1.63) и (3.1.70).

Наконец, из условия нормировки

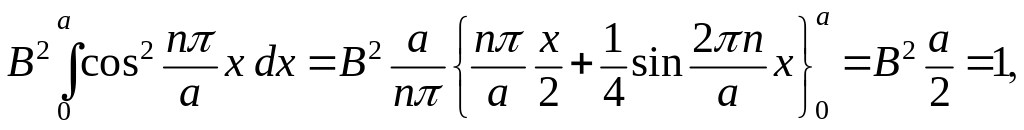(3.1.79)

получаем

Решив одномерную задачу, легко можно обобщить полученные результаты на трехмерный случай. Не конкретизируя пока вида потенциальной ямы (в любом измерении она может быть бесконечной), принимаем

(3.1.80)

Задача по-прежнему стационарна

(3.1.81)

и поэтому ограничиваемся решением стационарного уравнения Шредингера

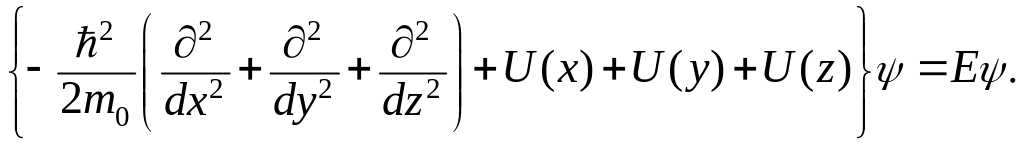(3.1.82)

При этом оказывается возможным разделение переменных. Полагая

(3.1.83)

из (3.1.82) получаем

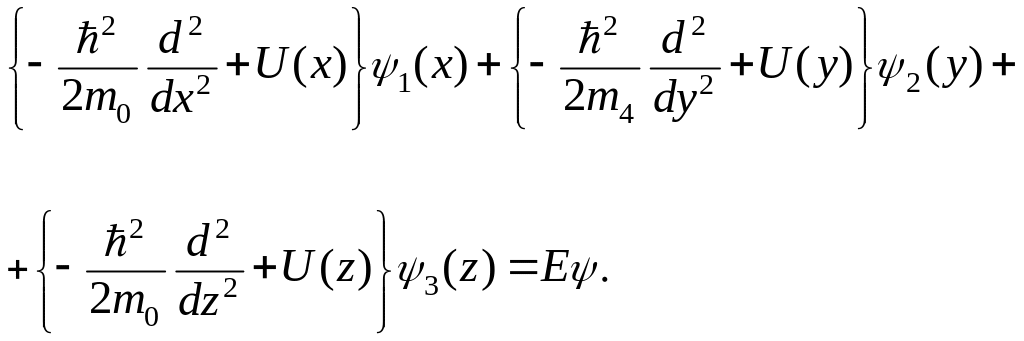(3.1.84)

Каждое функциональное слагаемое зависит здесь лишь от одной независимой переменной, и постоянство всей левой части возможно лишь при постоянстве каждого слагаемого. Вводя соответствующие постоянные, приходим к следующим независимым уравнениям :

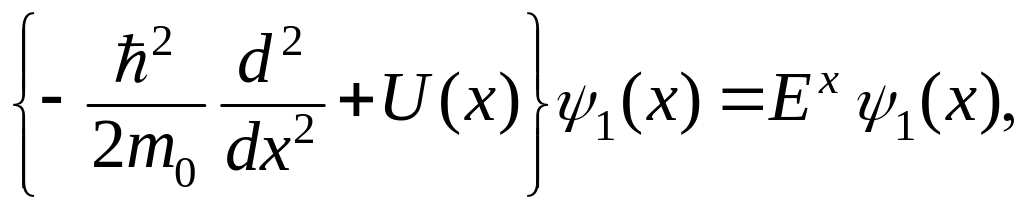
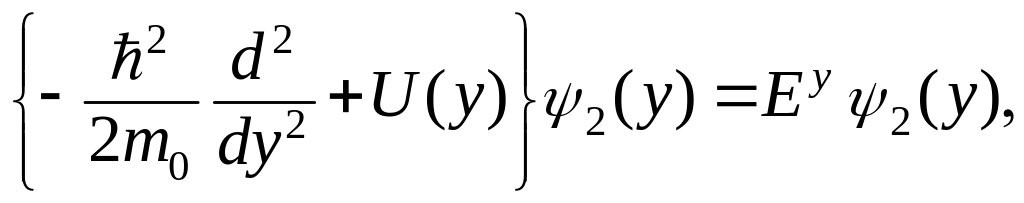(3.1.85)

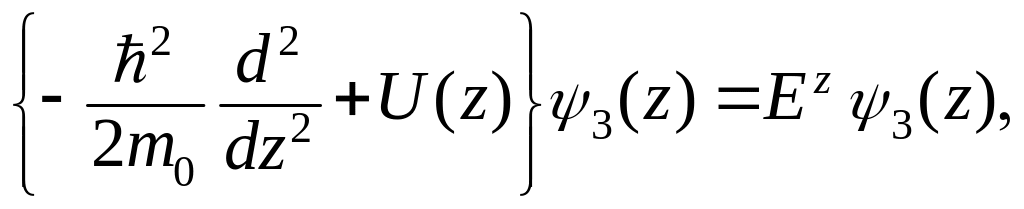
где , , – вклад в полную энергию от движения вдоль каждой координатной оси. Естественно, что

(3.1.86)

Таким образом, решение трехмерной задачи (частица в потенциальном ящике) свелась к решению уже известной одномерной задачи.

Рассмотрим для простоты бесконечно глубокую по всем измерениям потенциальную яму :

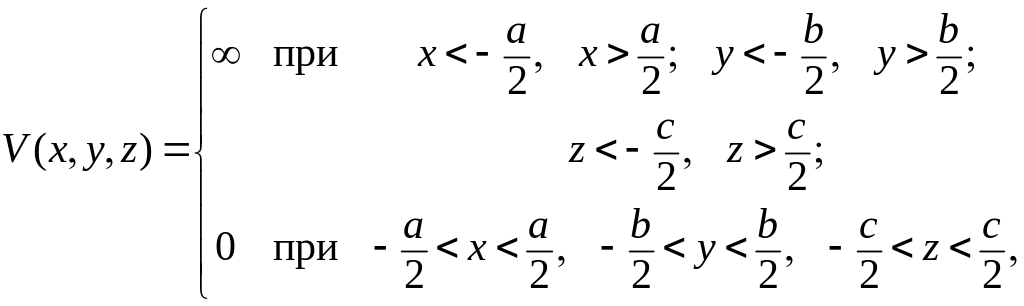(3.1.87)

или

(3.1.88)

Волновая функция (3.1.83) имеет вид

(3.1.89)

где

(3.1.90)

Аналогичный вид имеют и функции и .

Энергия состояния, характеризующегося волновой функцией (3.1.89), определяется тремя квантовыми числами :

. (3.1.91)

Полученное выражение для энергии наглядно может проиллюстрировать явление вырождения, которое заключается в том, что одному собственному значению оператора (в данном случае оператора энергии – гамильтониана) соответствует несколько собственных функций, или, что то же самое, имеется ряд состояний с одинаковой энергией. При произвольных размерах потенциальной ямы, когда , , , как правило, вырождения нет, т.е. при различных , , различны .

Однако при некоторых соотношениях между размерами ямы , , может быть вырождение. Например, если , , кратны друг другу. Пусть

(3.1.92)

Тогда

. (3.1.93)

Нетрудно видеть, что энергия одинакова, например, при следующих наборах квантовых чисел

1 2 3 1 3 2	4 6 4 6 4 2	9 3 6 6 3 9

(3.1.94)

Во всех этих различных состояниях полная энергия составляет

(3.1.95)

Аналогично, если, например,

(3.1.96)

энергия одинакова при следующих наборах квантовых чисел

1 2	12 6	5 10

(3.1.97)

и равна

(3.1.98)

Такое вырождение, не связанное с симметрией задачи, естественно назвать случайным; оно предопределено конкретным видом поля.

Укажем на возможность и так называемого естественного или симметрийного вырождения, имеющего место в связи с симметрией задачи. Пусть в случае трехмерной бесконечно глубокой потенциальной ямы

(3.1.99)

Тогда

(3.1.100)

Каждая степень свободы совершенно равноправно вносит свой вклад в энергию и, ввиду симметрии по всем измерениям, сами наименования , , носят условный характер. Все три направления эквивалентны. В связи с этим разным наборам квантовых чисел, например,

5 1 1	1 5 1	1 1 5

(3.1.101)

соответствует одинаковая энергия . Однако такую же энергию имеем и в случае . Если состояния (3.1.101) сводятся одно к другому переименованием координатных осей, т.е. эти состояния естественно вырождены (симметри йное вырождение), то состояние с имеет ту же энергию случайно, по совпадению (случайное или дополнительное вырождение).

Подчеркнем, что низший энергетический уровень не вырожден.

Таким образом, резюмируя, можно отметить, что при отсутствии симметрии может возникнуть лишь случайное вырождение, а при наличии симметрии имеет место, как симметрийное, так и случайное (дополнительное) вырождение.

Рассмотрим теперь движение частицы в одномерном случае с энергией, превышающей глубину симметричной потенциальной ямы.

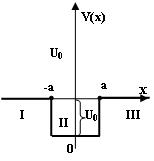
В этом случае более удобно перейти в другую (по сравнению с предыдущими задачами) систему координат. Зададим для этого потенциальную энергию в виде (см. рис. 3.5).

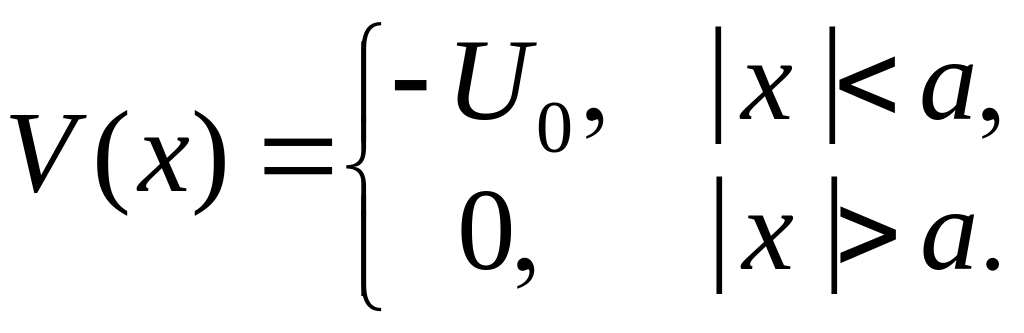(3.1.102)

Уравнение Шредингера для областей I, II, III принимает следующий вид

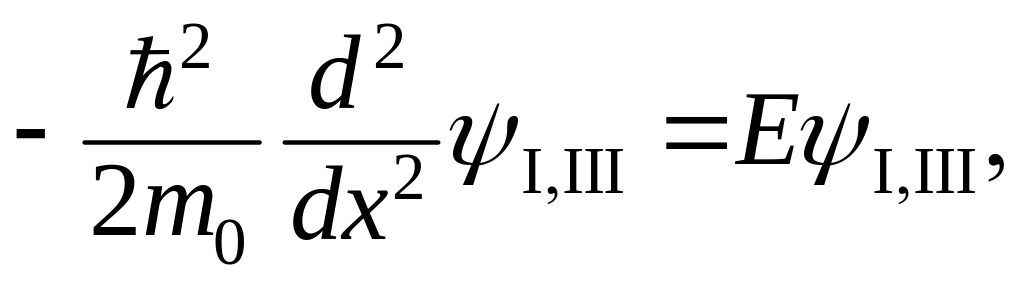
(3.1.103)

где , по постановке задачи. Вводя величины

(3.1.104)

преобразуем уравнения (3.1.103) к виду

(3.1.105)

Решения этих уравнений запишем в виде

(3.1.106)

Для того чтобы разобраться с константами, входящими в выражения общих решений, зададимся направлением полета частицы. Пусть частица движется из в . Находясь на бесконечном удалении от потенциальной ямы, частица свободна и описывается плоской волной де Бройля. Достигая потенциальной ямы, частица испытывает ее действие и, в частности, может либо пройти над ней в сторону положительных значений , либо отразиться обратно. Таким образом, в области I имеется две волны де Бройля – падающая и отраженная, тогда как в области III имеется только прошедшая волна. В связи с этим необходимо положить , т.е.

(3.1.107)

Для пяти констант , , , , , подлежащих определению, имеется только четыре граничных условия (четыре уравнения)

(3.1.108)

Поэтому данная система уравнений всегда имеет отличные от нуля решения. А поскольку в уравнения (3.1.108) через и входит единственный параметр решения , это означает, что движение возможно при любых положительных значениях энергии, т.е. спектр энергии будет непрерывным, сплошным. Этот факт можно было предположить и из инфинитности движения.

Запишем граничные условия (3.1.108) в явном виде. На границе имеем

(3.1.109a)

(3.1.109b)

Естественно, что, имея четыре уравнения (3.1.109) для пяти неизвестных, одну из постоянных, например , можно задать произвольно, а остальные – выразить через нее. Константа впоследствии может быть связана с нормировкой, причем ввиду инфинитности движения условие нормировки имеет вид

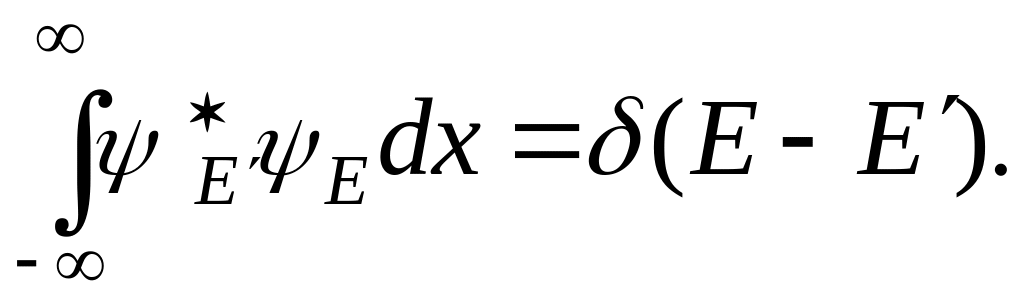(3.1.110)

Из уравнения (3.1.109b) выражаем константы , через :

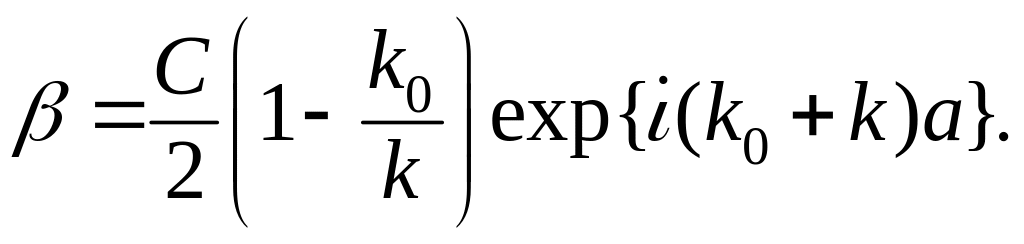(3.1.111)

Из уравнений (3.1.109a) находим

(3.1.112)

Подставляя в (3.1.112) , из соотношений (3.1.111), получаем

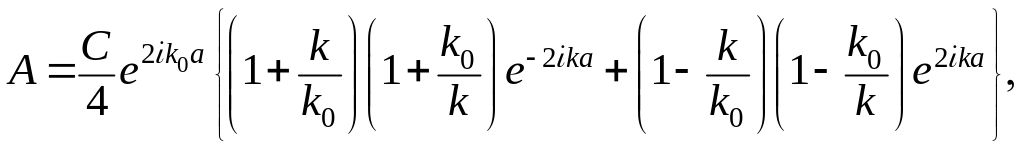
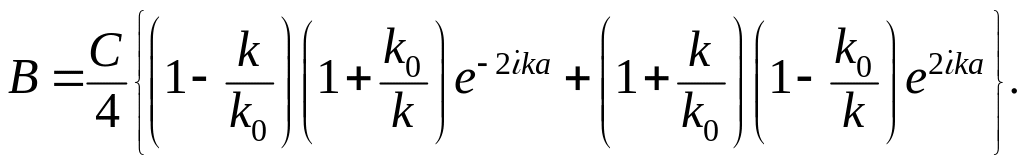(3.1.113)

Удобными характеристиками в такого рода задачах являются коэффициенты отражения и прохождения и :

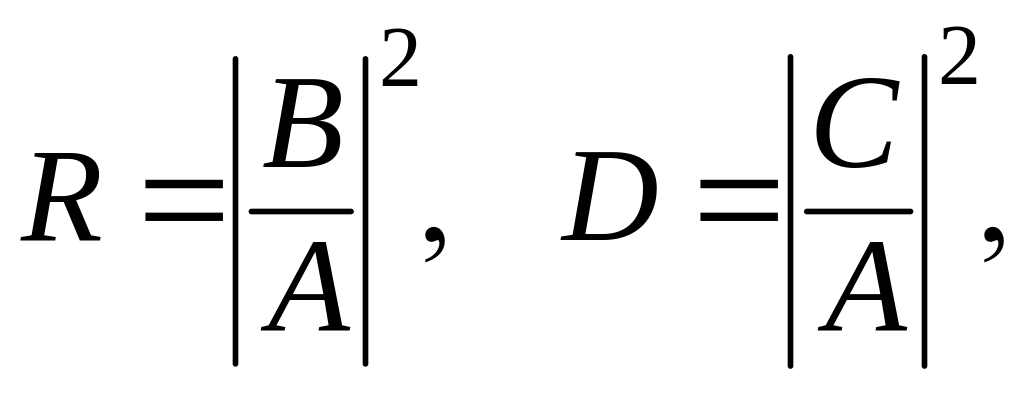(3.1.114)

сравнивающие интенсивности отраженной и прошедшей волн с интенсивностью падающей волны.

В связи с этим заметим, что для плотностей токов вероятности в областях I и III имеем соответственно

(3.1.115)

Из требования непрерывности плотности тока вероятности следует

(3.1.116)

откуда приходим к утверждению

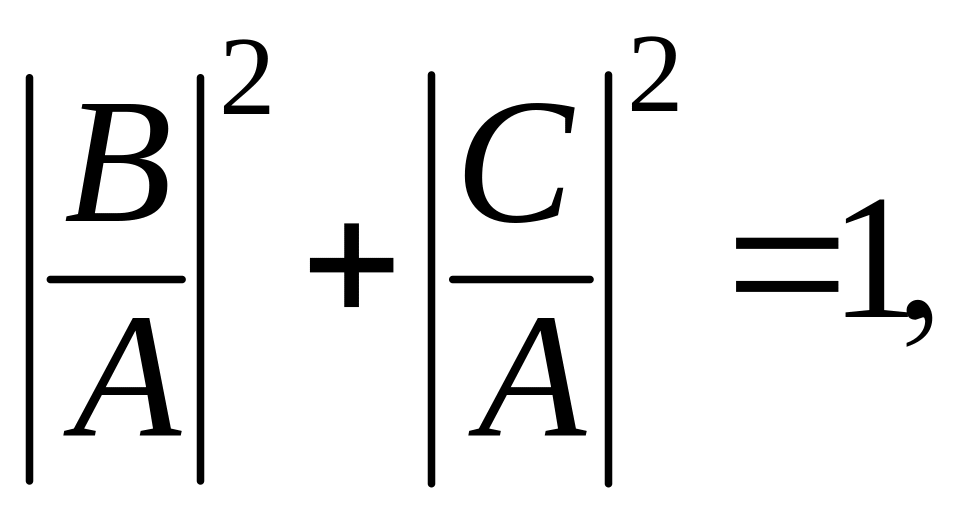(3.1.117)

т.е. сумма коэффициентов прохождения и отражения равна единице. Этот факт является проявлением закона сохранения материи, связанным с уравнением неразрывности.

Из (3.1.113) получаем

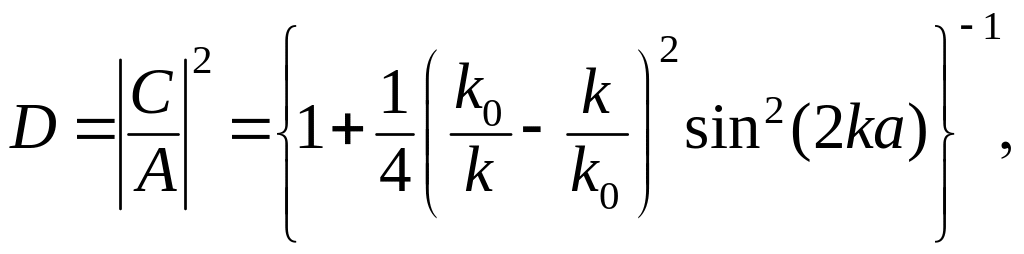(3.1.118)

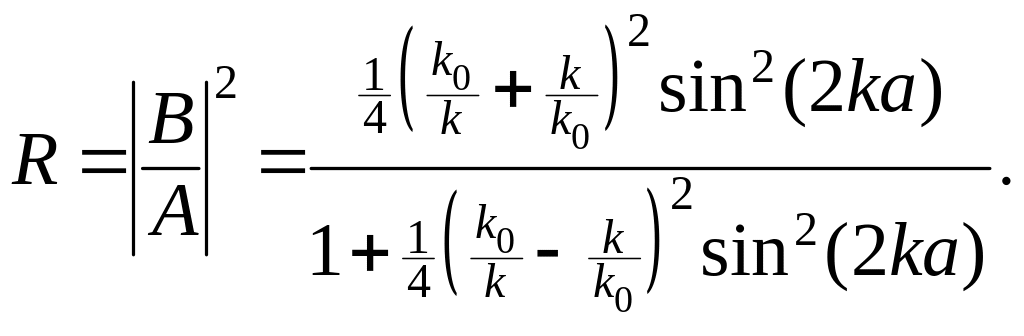(3.1.119)

Из этих выражений вытекают следующие очевидные факты. Если глубину ямы устремить к нулю, т.е. , коэффициент прохождения устремится к единице. Это естественно, так как исчезает причина отражения.

Однако и в случае ямы, когда , имеется такая возможность. В общем случае следует отметить, что при коэффициент прохождения не равен единице, т.е. имеется отличная от нуля вероятность отражения частицы от потенциальной ямы. (Заметим, что такого не может быть в классической физике, ибо мы рассматриваем случай при всех значениях , т.е. нет точек поворота.) Однако при условии

(3.1.120)

где – целое число, коэффициент прохождения и .

Из (3.1.104) находим значение энергии, при которых нет отраженной волны

(3.1.121)

откуда

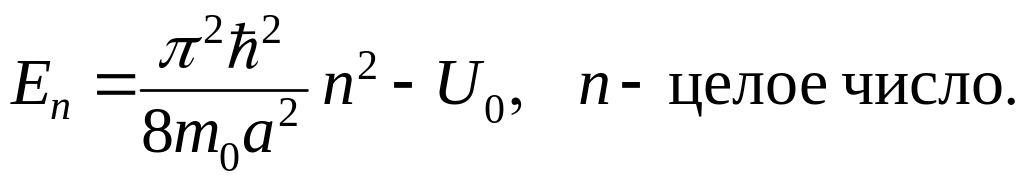(3.1.122)

При этих значениях энергии коэффициент прохождения равен единице. Их иногда называют резонансными энергиями. Согласно (3.1.119),

(3.1.123)

т.е. в яме при этом укладывается целое число полуволн де Бройля.

Заметим, что значения резонансных энергий (3.1.122) с точностью до выбора начала отсчета и масштаба ширины ямы совпадают со значениями энергетических уровней в бесконечно глубокой яме. В связи с этим (3.1.122) иногда называют виртуальными энергетическими уровнями.