Раздел 4
Спектральный анализ периодической последовательности радиоимпульса
Воспользуемся тем же соотношением (19) и (11), но для периодической последовательности:
(20)
Получим:
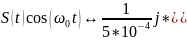(21)
рад/с
Рис. 8. Амплитудный спектр периодической последовательности радиоимпульсов
Проанализировав, полученные данные можно сделать выводы, что спектр последовательности радиоимпульсов представляет собой спектр периодического импульса, но «раздвоенного » и перенесенного в область высоких частот ± Спектр периодической последовательности радиоимпульсов дискретен.
Раздел 5 Корреляционный анализ непериодического сигнала
Корреляционный анализ – это анализ сигналов во временной области с целью выявления и оценки их подобия (сходства), основанный на изучении корреляционной функции (КФ). Длядетерминированных сигналов корреляция- понятие, которым отмечают связь между сигналами. Корреляционная функция дает количественную оценку степени этой связи.
Корреляционную функцию непериодического действительного сигнала S(t) с конечной энергией определяют по формуле:
(22)
Корреляционная функция
характеризирует меру сходства сигнала
с его копией
,
смещенной на интервал
.
Переменная
играет роль параметра;
- функия сдвига между сигналом и его
смещенной копией.
Найдем
корреляционную функцию сигнала (1)
используя формулу (22), учитывая что
принимает различные значения:
При
(рис.10,
Б)
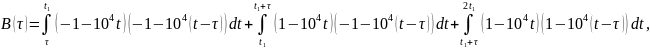где
Рассчитаем
полученный интегралы с помощь
математического ресурса в сети Интернет
Wolfram|Alpha
[Л4].
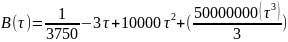
При
(рис.10,
В)
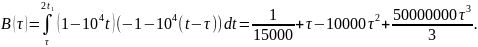График
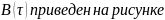(9). Здесь использовано свойство четности
КФ. Значение B(0)=E.
Из полученных данных следует, что функция афтокорреляции четная функция, имеющая максимум в точке 0, раный энергиии сигнала. При стремлении аргумента функции корреляции к бесконечности, сама функция стремится к нулю.
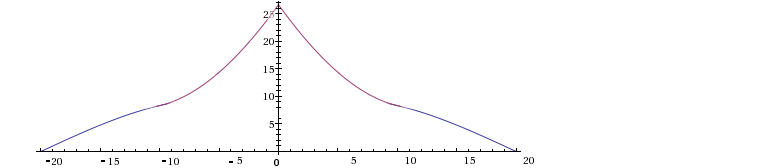
Р
ис.9
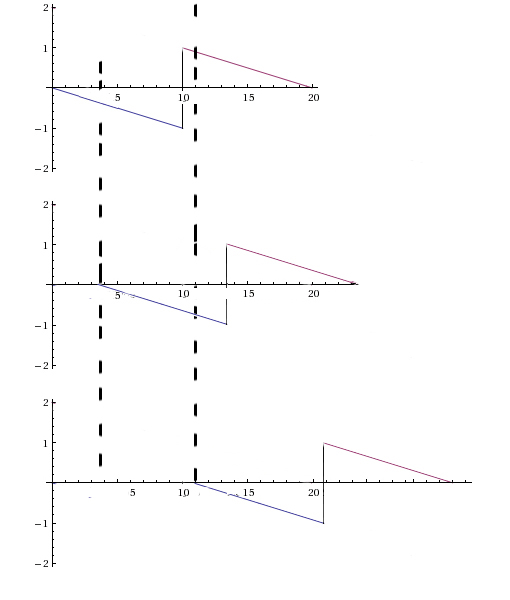
S(t)[B]
0
t
[с]
А)
S(t- )[B]
0 t [с] Б)
S(t- )[B]
0 В)
t [с]
Рис.10. Непериодический импульс (А)и его сдвинутые копии(Б,В)