Л-6 Определители

43

Лекция 6

4.6 Определитель произведения двух квадратных матриц.

Произведение двух квадратных матриц n-го порядка всегда определено. При этом важное значение имеет следующая теорема.

Теорема. Определитель матрицы-произведения равен произведению определителей матриц сомножителей:

Доказательство. Пусть

и ,

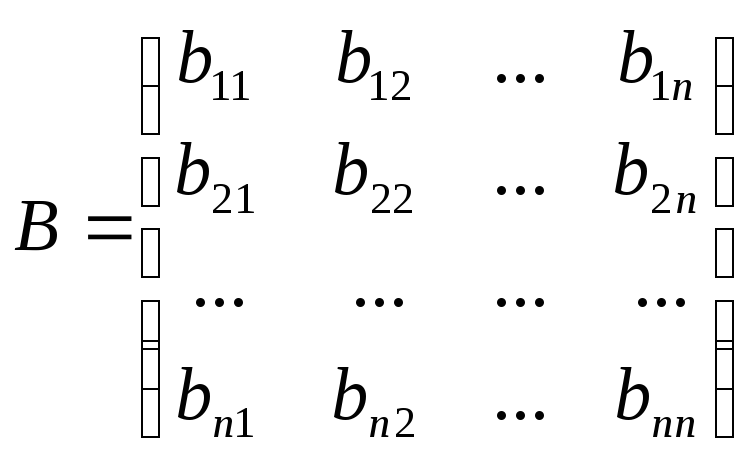тогда

.

Составим вспомогательный определитель

.

По следствию теоремы Лапласа имеем:

.

Итак, , покажем, что . Для этого преобразуем определитель следующим образом. Сначала первые п столбцов, умноженных соответственно на , прибавим к -му столбцу. Затем первые п столбцов, умноженных соответственно на , прибавим к -му столбцу и т.д. На последнем шаге к -му столбцу будут прибавлены первые п столбцов, умноженных соответственно на . В результате получим определитель

.

Разлагая полученный определитель с помощью теоремы Лапласа по последним п столбцам, находим:

Итак, доказаны равенства и , из которых следует, что .

4.7.Обратная матрица

Определение 1. Пусть дана квадратная матрица А п-го порядка. Квадратную матрицу того же порядка называют обратной к матрице А, если , где Е-единичная матрица п-го порядка.

Утверждение. Если существует матрица, обратная к матрице А, то такая матрица единственная.

Доказательство. Допустим, что матрица является не единственной матрицей, обратной к матрице А. Возьмем другую обратную матрицу В. Тогда выполняются условия

, .

Рассмотрим произведение . Для него имеют место равенства

,

,

из которых вытекает, что . Тем самым единственность обратной матрицы доказана.

При доказательстве теоремы о существовании обратной матрицы нам потребуется понятие «присоединенная матрица».

Определение 2. Пусть дана матрица

.

Матрица

элементами которой являются алгебраические дополнения элементов матрицы А , называется присоединенной матрицей к матрице А.

Обратим внимание на то, что для построения присоединенной матрицы С элементы матрицы А нужно заменить их алгебраическими дополнениями, а затем полученную матрицу транспонировать.

Определение 3. Квадратная матрица А называется невырожденной, если .

Теорема. Для того чтобы матрица А имела обратную матрицу , необходимо и достаточно, чтобы матрица А была невырожденной. При этом матрица определяется формулой

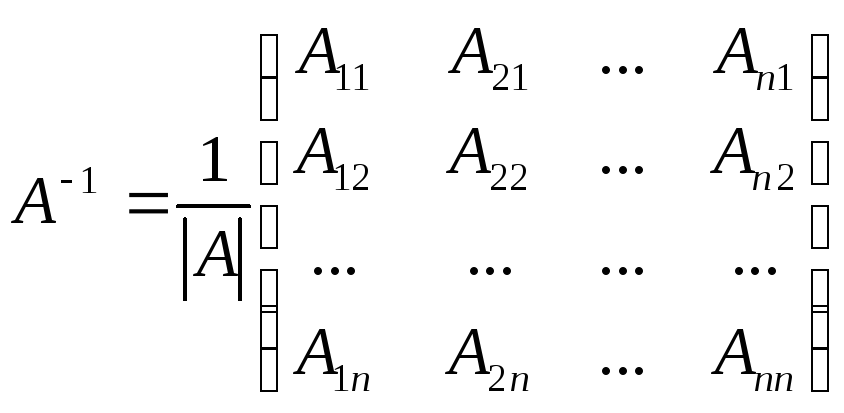, (1)

где - алгебраические дополнения элементов матрицы А.

Доказательство. Пусть матрица А имеет обратную матрицу . Тогда выполняются условия , из которых следует . Из последнего равенства получаем, что определители и . Эти определители связаны соотношением . Матрицы А и невырожденные, поскольку их определители отличны от нуля.

Пусть теперь матрица А невырожденная. Докажем, что матрица А имеет обратную матрицу и она определяется формулой (1). Дя этого рассмотрим произведение

матрицы А и присоединенной к ней матрицы С.

По правилу умножения матриц элемент произведения матриц А и С имеет вид: . Так как сумма произведений элементов i-й строки на алгебраические дополнения соответствующих элементов j-й строки равна нулю при и определителю при . Следовательно,

Поэтому

где Е – единичная матрица п-го порядка. Аналогично доказывается равенство . Таким образом, , а это означает, что и матрица является обратной к матрице А. Следовательно, невырожденная матрица А имеет обратную матрицу, которая определяется формулой (1).

Следствие 1. Определители матриц А и связаны соотношением .

Следствие 2. Основное свойство присоединенной матрицы С к матрице А выражается

равенствами .

Следствие 3. Определитель невырожденной матрицы А и присоединенной к ней матрицы

С связаны равенством .

Следствие 3 вытекает из равенства и свойства определителей, согласно которому при умножении на п-ю степень этого числа. В данном случае

,

откуда следует, что .

Пример. Найти матрицу, обратную к матрице А:

.

Решение. Определитель матрицы

отличен от нуля. Поэтому матрица А имеет обратную. Чтобы ее найти, сначала вычислим алгебраические дополнения:

, , ,

, , ,

, .

Теперь по формуле (1) запишем обратную матрицу

.

4.8. Элементарные преобразования над матрицами. Алгоритм Гаусса.

Определение 1. Под элементарными преобразованиями над матрицей размера

понимают следующие действия.

1. Умножение любой строки (столбца) матрицы на любое ненулевое число.

2. Прибавление к любой i-й строке матрицы любой ее j-й строки, умноженной на произвольное число.

3. Прибавление к любому i-му столбцу матрицы любого ее j-го столбца, умноженного на произвольное число.

4. Перестановка строк (столбцов) матрицы.

Определение 2. Матрицы А и В будем называть эквивалентными, если одна из них может быть преобразована в другую с помощью элементарных преобразований. Будем писать .

Эквивалентность матриц обладает следующими свойствами:

1. рефлективностью, т.е. ;

2. симметричностью, т.е. , то ;

3. транзитивностью, т.е. , , 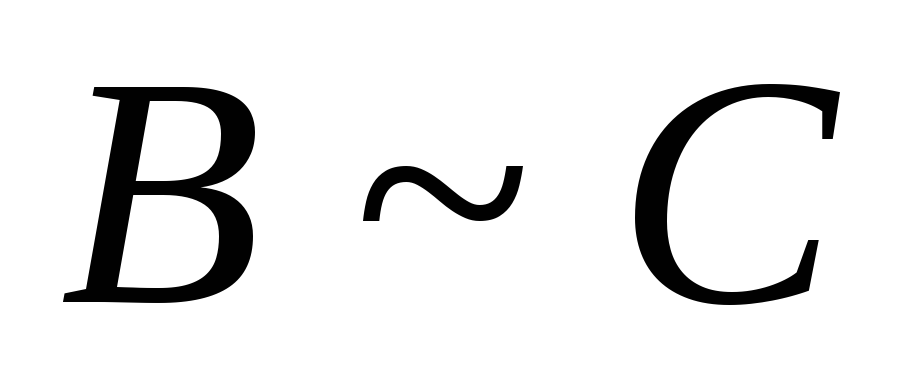то .

Определение 3. Ступенчатой называется матрица А обладающая следующими свойствами:

1) если i-я строка нулевая, т.е. состоит из одних нулей, то -я строка также нулевая;

2) если первые ненулевые элементы i-й и -й строк располагаются в столбцах с номерами k и l, то .

Пример. Матрицы

и

являются ступенчатыми, а матрица

ступенчатой не является.

Покажем, как с помощью элементарных преобразований можно привести матрицу А к ступенчатому виду.

Алгоритм Гаусса. Рассмотрим матрицу А размера . Без ограничения общности можем считать, что . (Если в матрице А имеется хотя бы отличный от нуля элемент, то перестановкой между собой строк, а затем столбцов можно добиться, чтобы этот элемент попал на пересечение первой строки и первого столбца.) Прибавим ко второй строке матрицы А первую, умноженную на , к третьей строке – первую, умноженную на и т.д.

В результате получим, что

.

Элементы в последних строках определяются формулами:

, , .

Рассмотрим матрицу

.

Если все элементы матрицы равны нулю, то

и эквивалентная матрица ступенчатая. Если среди элементов матрицы хотя бы один отличен от нуля, то можно без ограничения общности можно считать, что (этого можно добиться перестановкой строк и столбцов матрицы ). Преобразуя в этом случае матрицу так же как матрицу А, получим

соответственно,

.

Здесь , , .

Продолжая эти преобразования далее, получим на k-ом шаге, что

причем , , … , . В матрице А т строк и чтобы привести ее к ступенчатому виду указанным способом, понадобится не более т шагов. Далее процесс может оборваться на k-ом шаге в том и только в том случае, если все элементы матрицы

равны нулю. В этом случае

причем , , … , .

4.9. Отыскание обратной матрицы с помощью элементарных преобразований.

Для матрицы больших размеров отыскание обратной матрицы удобно проводить с помощью элементарных преобразований над матрицами. Этот метод состоит в следующем. Выписывают составную матрицу и по схеме метода Гаусса выполняют над строками этой матрицы (т.е. одновременно и в матрице А и в матрице Е) элементарные преобразования. В результате матрица А преобразуется в единичную матрицу, а матрица Е – в матрицу .

Пример. Найти матрицу, обратную к матрице

.

Решение. Запишем составную матрицу и преобразуем ее с помощью элементарных преобразований строк в соответствии с методом Гаусса. В результате получим:

.

Из этих преобразований заключаем, что

.

4.10 Ранг матрицы.

Определение. Целое число r называется рангом матрицы А, если у нее имеется минор порядка r, отличный от нуля, а все миноры порядка выше r равны нулю. Ранг матрицы будем обозначать символом .

Вычисляется ранг матрицы методом окаймления миноров.

1. Найти ненулевой элемент матрицы (если такого нет, то ранг равен нулю);

2. Вычислить миноры 2-го порядка, которые окаймляют выбранный элемент.

3. Если среди вычисленных миноров второго порядка имеется отличный от нуля, рассмотреть все миноры третьего порядка, окаймляющие какой-нибудь минор 2-го порядка, не равный нулю. Продолжая так до тех пор, пока все миноры, окаймляющие ненулевой минор k-го порядка, не будут равны нулю. В этом случае ранг матрицы .

Пример. Методом окаймляющих миноров вычислить ранг матрицы

.

Решение.

1. Находим ненулевой элемент матрицы, пусть это будет . Значит .

2. Вычисляем миноры 2-го порядка, окаймляющие выбранный элемент. , следовательно .

3. Вычислим миноры 3-го порядка, окаймляющие минор . Их всего два , , поэтому .

Указанный выше способ не всегда бывает удобным, т.к. связан с вычислением большого

количества определителей.

Утверждение. Ранг матрицы не изменяется при элементарных преобразованиях ее строк и столбцов.

Сформулированное утверждение указывает второй способ вычисления ранга матрицы. Он называется методом элементарных преобразований. Для отыскания ранга матрицы нужно методом Гаусса привести ее к ступенчатому виду, а затем выделить максимальный ненулевой минор. Поясним это на примере.

Пример. С помощью элементарных преобразований вычислить ранг матрицы

.

Решение. Выполним в соответствии с методом Гаусса цепочку элементарных преобразований. В результате получим цепочку эквивалентных матриц: