Оглавление

Оглавление 4

Ведение 6

Раздел 1 7

Спектральный анализ непериодического сигнала 7

Раздел 2 10

Спектральный анализ периодического сигнала 10

Раздел 4 14

Раздел 5 15

Корреляционный анализ непериодического сигнала 15

Раздел 6 18

Анализ прохождения непериодического сигнала через линейную цепь 18

Заключение 20

Список литературы 21

Ведение

Возможны два подхода к описанию сигналов: временной и частотный. При временном описании применяются известные математические функции, наиболее точно описывающие форму сигнала. Временное описание позволяет определить такие важные характеристики, как энергия, мощность и длительность сигнала.

Наряду с временным описанием сигналов широко используют частотный подход, при котором сигнал представляется в виде совокупности гармонических колебаний, имеющих различные частоты. Такой эквивалент сигнала –совокупность его гармонических составляющих называют спектром сигнала.

Целью данной работы является определение спектра сигнала для последующего спектрального анализа .

Объектом работы выступает сигнал, анализ которого является целью работы. Предмет работы - изучение методов спектрального анализа периодических и непериодических сигналов,радиоимпульсов, а так же анализ сигнала при прохождении его через линейную цепь. Ключевым методом анализа является представление сигнала в частотной области.

Целью первого раздела курсовой работы является нахождение спектральной плотности непериодического сигнала, для нахождения спектральной плотности используются теоремы спектрального анализа или свойства преобразования Фурье.

Целью второго раздела курсовой работы является нахождение спектра периодического сигнала, используя результаты первого раздела(спектральная плотность) и взаимосвязь спектров периодических и непериодических сигналов.

Целью третьего раздела курсовой работы является нахождения спектральной плотности радиоимпульса, используя свойства преобразования Фурье.

Целью четвертого раздела курсовой работы является нахождение спектра последовательности радиоимпульсов, используя свойства преобразования Фурье.

Целью пятого раздела является нахождение автокорреляционной функции сигнала и построение его графика.

Целью шестого раздела является нахождение спектральной функции на выходе линейной цепи.

Раздел 1 Спектральный анализ непериодического сигнала

Задан непериодический импульс (см. рис. 1):

S(t)= (1)

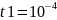где c.

Рис. 1. Заданный непериодический импульс

Определим спектральную плотность заданного сигнала, используя свойства преобразования Фурье [Л1], а именно свойство дифференцирования во временной области:

, (2)

где есть спектральная плотность непериодического импульса (1).

Продифференцируем заданный сигнал во временной области и изобразим его производную графически (см. рис. 2).

[B]

t [c]

2*δ(t)

Рис. 2. Производная непериодического импульса (1)

На рисунке 2 представлен одиночный прямоугольный импульс, спектральная плотность, которого известна [Л2]:

, (3) где => = -2*sinc(

Заданный сигнал (1) имеет скачок в точке t=0 (см. рис. 1). Производная от скачка есть дельта-функция, спектр которой равен [Л3]:

(4) Используя свойство линейности, получим спектральную плотность сигнала, изображенного на рис. 2.

. (5)

Так как производная заданного сигнала (рис.1), есть непериодический прямоугольный импульс (рис. 2), спектральную плотность которой мы знаем (3), то воспользовавшись свойством дифференцирования получим спектральную плотность заданного сигнала:

,

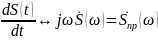т.е дифференцированию сигнала во временной области соответствует умножение его спектра на .

Отсюда, => , (6)

Амплитудный и фазовый спектр

Амплитудный спектр непериодического сигнала – зависимость модуля спектральной плотности амплитуд от частоты:

(7)

Воспользовавшись графопостроителем [Л4], построим амплитудный спектр (см. рис. 3).

Рис. 3. Амплитудный спектр непериодического сигнала (1)

Учитывая, что мнимая единица , входящая в (6), есть 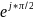, то фазовый спектр определим следующим образом:

(8)

Построим график фазового спектра (рис. 4).

0

Рис. 4. Фазовый спектр нереодического сигнала (1)

На основе полученных данных сделаем выводы об спектре одиночного видеоимпульса:

• Спектр сплошной

• Спектр двухсторонний

• Спектр бесконечный

• Спектр есть четная функция

• Фазовый спектр представляет собой сплошную,бесконеную, двухстороннюю и нечетную функцию.