6.Миноры и алгебраические дополнения.Теорема о разложении о-ля по рядам элементов.
Минор-определитель матрицы n-порядка,полученный из данной,путем вычеркивания строки и столбца,на пересечении которых стоит элемент,для которого находится Минор.
Алгебраическое дополнение-Минор,помноженный на (-1)m+n,где m-номер столбца; n-номер строки.
Определитель матрицы так же можно найти путем суммирования произведений элементов столбцов на их алгебраическое дополнение.
Det A=∑ amnxAmn ,где m-номер столбца;n-номер строки
7.Обратная матрица. Свойства обратных матриц.
Обратная матрица A-1 от A такая,что их произведение равно E.
A-невырожденная(определитель не равен нулю.
Свойства обратных матриц.
Det A-1=1/DetA
(AB)-1=A-1B-1-для двух любых обратимых матриц А и В.
(Ат)-1=(А-1)т
(kA)-1=k-1A-1
Для k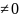
8.Ранг и базисный минор матрицы.
Ранг матрицы- наибольший порядок Минора, отличного от нуля.
Свойства рангов:
Ранг нулевой матрицы равен нулю.
Ранг Матрицы равен рангу транспонированной матрицы.
Если матрица n-порядка невырожденная, то ранг равен n.
Если матрица получена из другой матрицы методом элементарных преобразований, то их ранги равны.
Базисный минор- отличный от нуля Минор, порядок которого равен рангу матрицы.
Базисные неизвестные при этом- коэффициенты, образующие базисный минор.
9.Система Линейных уравнений
ax1+ax2+ax3+ax4=b
Записанная в виде матрицы m- количество уравнений, n- количество неизвестных.
Х-неизвестные, которые нужно найти, а – коэффициенты, b –свободные члены системы
Cистема однородна, если b=0
Квадратна, если m=n
Решение системы такие числа, которые при подстановке вместо х, выполняют тождества.
Система совместна если имеет хотя бы одно решение.
a1;a2;a3;an –линейно зависимы, если в a1х1+a2х2+a3х3+anхт=0 при хi=0
Матричный способ решения
=
;
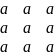
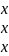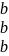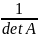* Матрица a
* матрица b
= матрица x
10.Слу. Метод Краммера.
* Матрица a * матрица b = матрица x
* (Матрица a
* матрица b)
=
*
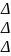,где дельта- определитель, полученный
из определителя det
A
путем замены в нем cоответствующего
номеру столбца на свободные члены.
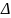X1=
1/
X2= 2/ , где дельта = det A
X3= 3/
11.Слу. Метод Гаусса. Метод Кронкера-Капелли.
Метод Гаусса заключается к вычеркиванию строк/ столбцов матрицы путем умножения строк/ столбцов на число и сложения с дургими с/с, для вычеркивания оных.
Метод К-К:
= , где 1- гл. матрица системы; 2- расширенная матрица системы.
1
2
Если ранг главной матрицы системы равен рангу расширенной матрицы системы, то система имеет решения. Если количество корней и количество неизвестных совпадает, система имеет единое решение, если нет- множество решений.
12.Однородные слу. Фундаментальная система решений.
Если ранг матрицы равен количеству корней, система имеет единое тривиальное решение.
Если количество корней меньше количества неизвестных, система имеет бесконечно количество решений.
Если имеется два различных решения, их линейная комбинация является системой однородных решений.
Найденные корни- базисные неизвестные, ненайденные-свободные.
Если свободным неизвестным придавать другие решения- система называется фундаментальной.
Пример*