31.Шум квантования

SNR - Signal-to-Noise Ratio ( отношение «сигнал-шум»).

Band Width

Oversampling

32. Реальные ацп и цап. Влияние помех. Источники шума

Шумы:

• Наводки на вх. цепи

• Внутренние шумы АЦП

• Искажения

• Ограничение полосы частот

• Дрожание

АЦП:

• Шумы квантования

• Искажения, связанные с интегр. и диф. нелинейностью

УВХ – устройство выборки и хранения для уменьшения динамической погрешности.

33. Основные динамические характиристики ацп (перечислить)

Основными динамическими параметрами АЦП являются время или максимальная частота преобразования.

Время преобразования t_пр - время от момента изменения сигнала на входе до появления на его выходе соответствующего устойчивого кода.

Максимальная частота преобразования f_прmах - наибольшая частота дискретизации, при которой выбранные параметры АЦП соответствуют нормам.

Апертурное время t_а - время между моментом выборки (отсчета) мгновенного значения и моментом получения его цифрового эквивалента.

Апертурная погрешность U_а определяется приращением входного изменяющегося во времени сигнала АЦП за время преобразования.

=====

Основные динамические характеристики АЦП:

1. THD (Total Harmonic Distortion) – гармонические (нелинейные) искажения.

2. Worst Harmonic – худшая гармоника

3. THD+N – общ. Гармонические искажения + шумы (Noise)

4. SNR

5. SNR+D (SINAD) – signal-to-noise distortion ratio

6. ENOB – effective number of bits – эффективное число бит

7. Аналоговая полоса пропускания – Analog BW

• Full-Power – полного диапазона (сигнал)

• Small-Signal – малый сигнал (порядок 10÷30%)

8. Интермодуляционные искажения – Intermodulation Distortion (IMD)

9. SFDR – динамич. Диапазон свободный от гармоник – Spurious Free Dynamic Range/

34. THD, THD+N, Worst Harmonic

THD

Нелинейность в результатах преобразования данных приводит к появлению гармонических искажений. Такие искажения наблюдаются как "выбросы" в спектре частот на четных и нечетных гармониках измеряемого сигнала. Эти искажения определяют как общие гармонические искажения (THD).

Суммарный коэффициент гармоник (THD) — это отношение среднеквадратического значения суммы гармоник к среднеквадратическому значению основной гармоники, выраженное в децибелах. Определяется по формуле

где V1 — среднеквадратическое значение основной гармоники, a V2...Vn —

среднеквадратические значения гармоник. Обычно = 6 или 9.

Величина гармонических искажений уменьшается на высоких частотах до точки, в которой амплитуда гармоник становится меньше, чем уровень шума.

THD – Total Harmonic Distortion (коэффициент нелинейных искажений) - равен квадратному корню отношения суммы мощностей всех гармоник, кроме основной, к мощности основного колебания. Согласно установившейся практике подаётся сигнал частотой 1 кГц максимальной амплитуды. Характеризует нелинейность и обычно сильно зависит от частоты.

THD+N – Total Harmonic Distortion + Noise — полный коэффициент гармоник с учётом шумов (для совместной оценки шумов и искажений).

Worst Harmonic – худшая гармоника.

=================================

СКЗ 1 – СКЗ 1-ой гармоники

(0 F_s/2) – число гармоник

Worst Harmonic – худшая гармоника.

35. SNR, SNR+D, ENOB.

Отношение "сигнал/шум" (SNR) - это отношение среднеквадратического значения величины входного сигнала к среднеквадратическому значению величины шума (за исключением гармонических искажений), выраженное в децибелах:

SNR(dB) = 20 log [ Vsignal(rms)/ Vnoise(rms) ]

Это значение позволяет определить долю шума в измеряемом сигнале по отношению к полезному сигналу.

Шум, измеряемый при расчете SNR, не включает гармонические искажения, но включает шум квантования. Для АЦП с определенным разрешением именно шум квантования ограничивает возможности преобразователя теоретически лучшим значением отношения сигнал/шум, которое определяется как:

SNR(db) = 6.02 N + 1.76, где N - разрешение АЦП.

Основные понятия. S/N +D

Signal-to-Noise (SNR) Ratio – отношение «сигнал-шум». Очень важная характеристика. Даже в идеальном АЦП есть шум, и меньше некоторого значения нельзя сделать отношение «сигнал-шум».

SNR = 20log U₁/U_Ш U₁-среднеквадратическое значение sin

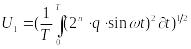
Uшума = q/√3

SNR = 20nlog2+10log1,5=6,02n+1,76 [дб] n-число двоичных разрядов

Лучше этого значения не удастся получить. Из этой формулы можно найти эффективной значение n.

Signal-to-Noise and Distortion (SNR+D) Ratio – учитываются все возможные шумы и искажения. Эти данные обычно приводятся в справочниках.

Отношение сигнала (суммарное значение коэффициента нелинейных искажений + шум) (Signal-to-THD Plus Noise) – отношение среднеквадратического значения тестового сигнала (синусоиды) к среднеквадратическому значению уровня остаточных гармонических искажений и шума. Эта характеристика должна включать уровень входного сигнала, используемого для определения характеристики полосы пропускания, в которой производится измерение характеристики.

Основные понятия.ENOB

ENOB (Effective Number of Bits) — эффективное количество разрядов преобразователя, определяемое соотношением сигнал/шум. Из-за постоянства величины шума и падения коэффициента передачи АЦП на высоких частотах этот параметр зависит от уровня преобразуемого сигнала и его частоты (для синусоидального сигнала). Иногда вместо этого параметра указывают отношение сигнал/шум (SNR). Учитывая, что в большинстве случаев шум является белым, ENOB и отношение сигнал/шум связаны следующей формулой:

В этой формуле предполагается, что уровень нелинейных искажений мал по сравнению с уровнем шумов.

В справочниках приводятся значения ENOB, достигаемые при определенных условиях, и разработчику следует учитывать возможное ухудшение этого параметра при уменьшении входного сигнала.

Однако увеличение ENOB за счет увеличения уровня входного сигнала ограничивается ростом нелинейности передаточной характеристики АЦП. В общем случае вместо отношения сигнал/шум в формулу следует подставить величину параметра SINAD, т.е. отношение уровня сигнала к сумме шумов и гармонических искажений.

Отношение "сигнал/шум и искажения" (SiNAD) более полно описывает шумовые характеристики АЦП. SiNAD учитывает величину как шума, так и гармонических искажений по отношению к полезному сигналу. SiNAD рассчитывается по следующей формуле:

35 SNR, SNR+D, ENOB

SNR – Signal-to-Noise Ratio (отношение сигнал-шум) — показывает превышение амплитуды выходного сигнала над среднеквадратичным значением мощности шумов.

n – количество разрядов АЦП. Следовательно, отношение сигнал-шум увеличивается с увеличением разрядности.

SNR+D – Signal-to-Noise Distortion Ratio (или SINAD) — отношение уровня сигнала к сумме уровней сигнала, шумов и продуктов искажения сигнала.

ENOB – Effective Number Of Bits (Эффективное число разрядов) — количество информации (количество разрядов ENOB), которое реальный АЦП может извлечь из входного сигнала.

===========

дБ

(всех шумов)

36. SFDR.IMD

SFDR (Spurious-Free Dynamic Range) — динамический диапазон, свободный от гармоник — это еще один важный параметр, характеризующий высокочастотные параметры АЦП.

Динамический диапазон, свободный от гармоник, представляет собой разницу между величиной измеряемого сигнала и наибольшим пиком искажений. Он ограничен снизу амплитудой максимальной гармоники паразитных выбросов на выходе АЦП в диапазоне его рабочих частот.

Следует понимать, что зачастую максимальным уровнем обладают не кратные гармоники, а результаты отображения в первую зону Найквиста результатов перемножения основного сигнала с шумовым или помеховым сигналом (например, с гармониками тактового сигнала). Фактически этот параметр характеризует все возможные следствия нелинейности передаточной характеристики АЦП и аналоговой части тракта преобразователя при работе с ВЧ-сигналом. Во многих случаях именно величина SFDR, а не уровень шумов ограничивает возможности АЦП.

IMD

Интермодуляционные искажения (IMD). Когда на вход АЦП подается сигнал, представляющий собой сумму двух синусоид с разными частотами, то вследствие нелинейности характеристики преобразования, в выходном коде будут присутствовать составляющие с суммарными и разностными частотами

Интермодуляционными членами называются те, для которых ни m, ни n не равны нулю. Например, члены второго порядка это , а члены третьего порядка — это и .

Если АЦП тестируется с использованием международного стандарта CCIF, то на его вход подаются две синусоиды с частотами вблизи верхней граничной частоты входного сигнала. В этом случае частоты членов 2-го и 3-го порядка имеют существенно различные значения. Члены 2-го порядка обычно значительно отстоят по частоте от входных синусоид, тогда как частоты членов 3-го порядка обычно близки к входным частотам. Вследствие этого члены 2-го и 3-го порядка в спецификациях указываются отдельно.

IMD вычисляется аналогично TND и равно отношению среднеквадратических значений суммы отдельных интермодуляционных искажений к среднеквадратическому значению основной гармоники, выраженному в дБ.

36 SFDR, IMD

SFDR - Spurious-Free Dynamic Range (динамический диапазон, свободный от паразитных составляющих) - отношение мощности полезного узкополосного сигнала (несущей) к мощности наиболее мощной паразитной частотной составляющей. Обычно выражается в децибелах.

IMD – Two-Tone Intermodulation Distortion (Интермодуляционные искажения) - нелинейные искажения, создаваемые усилительными схемами. В частотном спектре двухтонального сигнала с интермодуляционными искажениями содержатся комбинационные составляющие с частотами, являющимися суммой и разностью основных и гармонических частот входных сигналов. Например, при подаче на усилитель смеси сигналов 1 кГц и 5 кГц возникают интермодуляционные искажения: 6 кГц (сумма 1 кГц и 5 кГц) и 4 кГц (разность между 1 кГц и 5 кГц). Эти продукты интермодуляционных искажений взаимодействуют друг с другом, создавая практически бесконечный ряд частотных составляющих.

===

IMD :

На вход АЦП подаются 2 синусоидальных сигнала примерно одинаковой частоты, но разной амплитуды => возникают дополнительные частоты:

2-го порядка – f₁± f₂ , 2 f₁ и 2 f₂

3-го порядка - f₁±2 f₂ , 3 f₁ , 3 f₂ , f₂ ±2f₁

Наиболее сложно отфильтровать f третьего порядка. Гармоники в основном появляются из-за интегральной нелинейности.

IMD чаще всего оцениваются, где работают со звуком.