Квадратичные формы.
Определение. Квадратичной формой L (x1, x2, …, xn) от n переменных называется сумма, каждый член которой является либо квадратом одной из переменных, либо произведением двух разных переменных, взятых с некоторым коэффициентом:
Предполагаем, что коэффициенты квадратичной формы aij – действительные числа, причем aij = aji. Матрица A = (aij) (i, j = 1, 2, …, n), составленная из этих коэффициентов, называется матрицей квадратичной формы.
В матричной записи квадратичная форма имеет вид:
L = X'AX,
где X = (x1, x2, …, xn)' – матрица-столбец переменных.
Приведение квадратичной формы к каноническому виду.
Квадратичная
форма
называется канонической (или имеет
канонический вид), если все ее коэффициенты
aij
= 0 при i
j:
а ее матрица является диагональной.
Теорема. Любая квадратичная форма с помощью невырожденного линейного преобразования переменных может быть приведена к каноническому виду.
Положительно и отрицательно определенные квадратичные формы.
Квадратичная форма L (x1, x2, …, xn) называется положительно (отрицательно) определенной, если при всех значениях переменных, из которых хотя бы одно отлично от нуля,
L (x1, x2, …, xn) > 0 (L (x1, x2, …, xn) 0).
Теорема. Для того чтобы квадратичная форма L = X'AX была положительно (отрицательно) определенной, необходимо и достаточно, чтобы все собственные значения λi матрицы A были положительны (отрицательны).
Теорема. Для того чтобы квадратичная форма была положительно определенной, необходимо и недостаточно, чтобы все главные миноры матрицы этой формы были положительны, т.е. 1 > 0, 2 > 0, …, n > 0, где
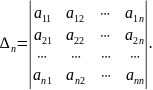
Следует отметить, что для отрицательно определенных квадратичных форм знаки главных миноров чередуются, начиная со знака «минус» для минора первого порядка.
Линейная модель обмена.
В качестве примера математической модели экономического процесса, приводящейся к понятию собственного вектора и собственного значения матрицы, рассмотрим линейную модель обмена (модель международной торговли).
Пусть имеется n стран S1, S2, …, Sn, национальный доход каждой из которых равен соответственно x1, x2, …, xn. Обозначим коэффициентами aij долю национального дохода, которую страна Sj тратит на покупку товаров у страны Si. Будем считать, что весь национальный доход тратится на закупку товаров либо внутри страны, либо на импорт из других стран, т.е.
Рассмотрим
матрицу
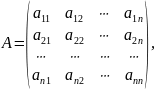
которая получила название структурной матрицы торговли. Сумма элементов любого столбца матрицы A равна 1.
Для любой страны Si (i = 1, 2, …, n) выручка от внутренней и внешней торговли составит:
pi = ai1x1 + ai2x2 + … + ainxn.
Для сбалансированной торговли необходима бездефицитность торговли каждой страны Si, т.е. выручка от торговли каждой страны должна быть не меньше ее национального дохода:
pi ≥ xi (i = 1, 2, …, n).
Если считать, что pi > xi (i = 1, 2, …, n), то получаем систему неравенств
Сложив все неравенства системы, получим после группировки
x1(a11 + a21 + … + an1) + x2(a12 + a22 + … + an2) + … + xn(a1n + a2n + … + ann) > x1 + x2 + … + xn.
Выражения в скобках равны единице, и мы приходим к противоречивому неравенству
x1 + x2 + … + xn > x1 + x2 + … + xn.
Таким образом, неравенство pi > xi (i = 1, 2, …, n) невозможно, и условие pi ≥ xi принимает вид pi = xi (i = 1, 2, …, n). (С экономической точки зрения это понятно, так как все страны не могут одновременно получать прибыль).
Вводя вектор x = (x1, x2, …, xn) национальных доходов стран, получим матричное уравнение
AX = X,
где X – матрица-столбец из координат вектора x, т.е. задача свелась к отысканию собственного вектора матрицы A, отвечающего собственному значению λ = 1.