16. Линейные операции над векторами.

Произведением вектора на число λ называется вектор , имеющий длину , направление которого совпадает с направлением вектора , если λ > 0, и противоположно ему, если λ  0.

Противоположным вектором называется произведение вектора на число (–1), т.е. .

Суммой двух векторов и называется вектор , начало которого совпадает с началом вектора , а конец – с концом вектора при условии, что начало вектора совпадает с концом вектора (правило треугольников).

Очевидно, что вектор в этом случае представляет диагональ параллелограмма, построенного на векторах и (правило параллелограмма).

Аналогично определяется сумма нескольких векторов. Так, например, сумма четырех векторов , , , есть вектор , начало которого совпадает с началом вектора , а конец – с концом вектора (правило многоугольника).

Разностью двух векторов и называется сумма вектора и вектора , противоположного .

17. Проекции вектора на ось, теоремы о проекциях.

Теорема (о проекции вектора на ось): проекция вектора на ось равна длине этого вектора, умноженной на косинус угла между вектором и осью.

Следствие: равные вектора имеют равные проекции на одну ось.

Теорема (о проекции суммы векторов): проекция суммы двух векторов на ось равна сумме проекций двух векторов на ту же ось.

Теорема (о проекции произведения скаляра на вектор): при умножении вектора на скаляр, его проекция на ось умножается на этот же скаляр.

18. Координаты вектора в пространстве, выражение линейных операций в координатной форме.

Координатами вектора в пространстве Oxyz являются три числа x, y и z ( = (x, y, z)).

Равенство векторов и линейные операции (сложение векторов и умножение вектора на число) удобно представлять в координатной форме. При этом справедливы следующие свойства.

1. Равные векторы имеют равные координаты (в одном и том же базисе).

2. Каждая координата суммы векторов равна сумме соответствующих координат слагаемых.

3. Каждая координата произведения вектора на число равна произведению этого числа на соответствующую координату вектора.

4. Каждая координата линейной комбинации векторов равна линейной комбинации соответствующих координат векторов.

19. Модуль вектора и его направляющие косинусы.

Множество векторов на прямой назовем одномерным векторным пространством R¹, множество векторов на плоскости – двумерным векторным пространством R², в пространстве – трехмерным векторным пространством R³. Пространство Rⁿ является системой содержащей всю бесконечную совокупность -мерных векторов.

В пространстве R³ обычно используют прямоугольную декартову систему координат Oxyz, где любая точка M пространства, имеющая координаты x (абсциссу), y (ординату) и z (аппликату), обозначается M (x, y, z).

Определение. Вектор , начало которого находится в начале координат, а конец в точке A (x₁, y₁, z₁), называют радиус-вектором точки A и обозначают или просто . Так как его координаты совпадают с координатами точки A, то его разложение по ортам имеет вид .

Вектор , имеющий начало в (∙) A (x₁, y₁, z₁), и конец в (∙) B (x₂, y₂, z₂), может быть записан в виде , где – радиус-вектор точки B; – радиус-вектор точки A.

Поэтому разложение вектора по ортам имеет вид:

Его длина равна расстоянию между точками A и B:

Свободный вектор, например , заданный в координатном пространстве Oxyz, может быть представлен в виде , где b_x, b_y, b_z – проекции вектора на соответствующие оси координат (координаты вектора), а , , – орты этих осей. Пишут .

Длина вектора (модуль вектора) определяется по формуле:

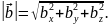
Направление вектора определяется углами , , , образованными им с осями координат Ox, Oy, Oz. Косинусы этих углов (направляющие косинусы вектора) вычисляются по формулам:

Тогда координаты вектора будут равны:

Подставив эти выражения в формулу вычисления длины вектора, установим, что направляющие косинусы вектора связаны соотношением:

Замечание. Координатами единичного вектора являются числа cos, cos, cos, то есть .