10. Матричный способ решения систем линейных уравнений.

Пусть число уравнений системы равно числу переменных, т.е. m=n. Тогда матрица системы является квадратной, а ее определитель =|A| называется определителем системы.

Рассмотрим решение системы двух уравнений с двумя переменными:

в которой хотя бы один из коэффициентов при переменных отличен от нуля.

Для решения этой системы исключим переменную x₂, умножив первое уравнение на a₂₂, второе – на (–a₁₂) и сложив их. Затем исключим переменную x₁, умножив первое уравнение на (–a₂₁), второе – на a₁₁ и также сложив их. В результате получим систему:

Выражение в скобках есть определитель системы

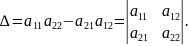
Обозначив , , 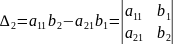система примет вид:

Из полученной системы следует, что если определитель системы 0, то система имеет единственное решение, определяемое по формулам: , .

Если =0, а ₁0 (или ₂0), то система несовместная, так как в этом случае приводится к виду:

Если =₁=₂=0, то система неопределенная и имеет бесконечное множество решений, так как в этом случае приводится к виду:

11. Формулы Крамера.

Теорема Крамера. Пусть  – определитель матрицы системы A, а _j – определитель матрицы, получаемой из матрицы A заменой j-го столбца столбцом свободных членов. Тогда, если 0, то система имеет единственное решение, определяемое по формулам:

12. Метод Гаусса.

Метод Гаусса – метод последовательного исключения переменных – заключается в том, что с помощью элементарных преобразований система уравнений приводится к равносильной системе ступенчатого (или треугольного) вида, из которой последовательно, начиная с последних (по номеру) переменных, находятся все остальные переменные.

13. Системы m линейных уравнений с n переменными, базисные допустимые решения.

Для совместных систем линейных уравнений верны следующие теоремы.

1. Если ранг матрицы совместной системы равен числу переменных, т.е. r = n, то система имеет единственное решение.

2. Если ранг матрицы совместной системы меньше числа переменных, т.е. r  n, то система неопределенная и имеет бесконечное множество решений.

14. Системы линейных однородных уравнений, свойства их решений.

Система m линейных уравнений с n переменными называется системой линейных однородных уравнений, если все их свободные члены равны нулю. Такая система имеет вид:

Система линейных однородных уравнений всегда совместна, так как она всегда имеет, по крайней мере, нулевое (или тривиальное) решение (0; 0; …; 0).

Система линейных однородных уравнений имеет ненулевые решения тогда и только тогда, когда ранг ее матрицы коэффициентов при переменных меньше числа переменных, т.е. при r(A)  n.

15. Модель Леонтьева многоотраслевой экономики.

Рассмотрим процесс производства за некоторый период времени (например, год).

Введем следующие обозначения: x_i – общий (валовой) объем продукции i-й отрасли (i = 1, 2, …, n);

x_ij – объем продукции i-й отрасли, потребляемой j-й отраслью в процессе производства (i, j = 1, 2, …, n);

y_i – объем конечного продукта i-й отрасли для непроизводственного потребления.

Так как валовой объем продукции любой i-й отрасли равен суммарному объему продукции, потребляемой n отраслями, и конечного продукта, то

Уравнения называются соотношениями баланса. Будем рассматривать стоимостный межотраслевой баланс, когда все величины, входящие в уравнения, имеют стоимостное выражение.

Введем коэффициенты прямых затрат

показывающие затраты продукции i-й отрасли на производство единицы продукции j-й отрасли.

Можно полагать, что в некотором промежутке времени коэффициенты a_ij будут постоянными и зависящими от сложившейся технологии производства. Это означает линейную зависимость материальных затрат от валового выпуска, т.е.

x_ij = a_ijx_j, (i, j = 1, 2, …, n),

вследствие чего построенная на этом основании модель межотраслевого баланса получила название линейной.

Теперь соотношения баланса примут вид:

Обозначим , , ,

где X – вектор валового выпуска, Y – вектор конечного продукта, A – матрица прямых затрат (технологическая или структурная матрица).

Тогда систему можно записать в матричном виде:

X = AX + Y.

Основная задача межотраслевого баланса состоит в отыскании такого вектора валового выпуска X, который при известной матрице прямых затрат A обеспечивает заданный вектор конечного продукта Y.

Перепишем уравнение в виде:

(E – A) X = Y.

Если матрица (E – A) невырожденная, т.е. |E – A|  0, то

X = (E – A)^–1Y.

Матрица S = (E – A)^–1 называется матрицей полных затрат.

Чтобы выяснить экономический смысл элементов матрицы S = (s_ij), будем задаваться единичными векторами конечного продукта Y₁ = (1, 0, …, 0)', Y₂ = (0, 1, …, 0)'. Тогда соответствующие векторы валового выпуска будут X₁ = (s₁₁, s₂₁, …, s_n1)', X₂ = (s₁₂, s₂₂, …, s_n2)', …, X_n = (s_1n, s_2n, … s_nn)'.

Следовательно, каждый элемент s_ij матрицы S есть величина валового выпуска продукции i-й отрасли, необходимого для обеспечения выпуска единицы конечного продукта j-й отрасли y_j = 1 (j = 1, 2, …, n).

В соответствии с экономическим смыслом задачи значения x_i должны быть неотрицательны при неотрицательных значениях y_i ≥ 0 и a_ij ≥ 0, где i, j = 1, 2, …, n.

Матрица A ≥ 0 называется продуктивной, если для любого вектора Y ≥ 0 существует решение X ≥ 0. В этом случае и модель Леонтьева называется продуктивной.