Матрицы, основные понятия.
Матрицей размера m×n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, A, B, C, …, а для обозначения элементов матрицы используются строчные буквы с двойной индексацией: aij, где i – номер строки, j – номер столбца.
Например, матрица
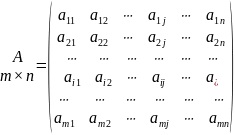
или, в сокращенной записи, A=(aij); i = 1, 2, …, m; j = 1, 2, …, n.
Алгебра матриц.
1. Умножение матрицы на число. Произведением матрицы A на число λ называется матрица B=λA, элементы которой bij=λaij для i = 1, 2, …, m; j = 1, 2, …, n.
Например,
если
,
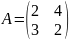то
.
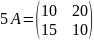Следствие. Общий множитель всех элементов матрицы можно выносить за знак матрицы.
Например,
.
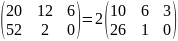В частности, произведение матрицы A на число 0 есть нулевая матрица, т.е. 0•A=0.
2. Сложение матриц. Суммой двух матриц A и B одинакового размера m×n называется матрица C = A + B, элементы которой cij = aij + bij для i = 1, 2, …, m; j = 1, 2, …, n (т.е. матрицы складываются поэлементно).
Например,
,
,
.
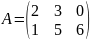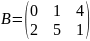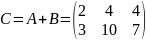В частном случае A+0=A.
3. Вычитание матриц. Разность двух матриц одинакового размера определяется через предыдущие операции: A–B=A+(–1)•B.
4. Умножение матриц. Умножение матрицы A на матрицу B определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц A•B называется такая матрица C, каждый элемент которой cij равен сумме произведений элементов i-й строки матрицы A на соответствующие элементы j-го столбца матрицы B:
,
i
= 1, 2, …, m;
j
= 1, 2, …, n.
5. Возведение в степень. Целой положительной степенью Am (m>1) квадратной матрицы A называется произведение m матриц, равных A, т.е.
.
Операция возведения в степень определяется только для квадратных матриц.
6. Транспонирование матрицы – переход от матрицы A к матрице A', в которой строки и столбцы поменялись местами с сохранением порядка. Матрица A' называется транспонированной относительно матрицы A:
,
.
Из определения следует, что если матрица A имеет размер m×n, то транспонированная матрица A' имеет размер n×m.
Например,
;
.
Определитель матрицы.
Определителем квадратной матрицы n-го порядка, или определителем n-го порядка, называется число, равное алгебраической сумме n! членов, каждый из которых является произведением n элементов матрицы, взятых по одному из каждой строки и каждого столбца, причем знак каждого члена определяется как (–1)r(J), где r(J) – число инверсий в перестановке J из номеров столбцов элементов матрицы, если при этом номера строк записаны в порядке возрастания:
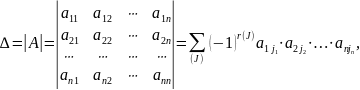
где сумма берется по всем перестановкам J.
Вычисление определителей второго и третьего порядка.
Определителем матрицы второго порядка A=(aij), или определителем второго порядка, называется число, которое вычисляется по формуле:
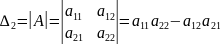
Определителем матрицы третьего порядка A=(aij), или определителем третьего порядка, называется число, которое вычисляется по формуле:
Теорема разложения.
Теорема Лапласа. Определитель квадратной матрицы равен сумме произведений элементов любой строки (столбца) на их алгебраические дополнения:
(разложение по элементам i-й строки; i = 1; 2; …; n);
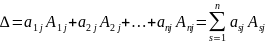
(разложение по элементам j-го столбца; j = 1; 2; …; n).