Вопрос 2.
Связь КФ входного воздействия и отклика ЛС для дискретного случая.
Пусть 
- ИХ ЦФ. Тогда отклик ЛС 
на последовательность 
на входе отпредеяется дискретной
сверткой
Среднее значение отклика
Для стационарного СП 
,
тогда получим 
Найдем КФ отклика
Если СП 
стационарное, то 
следовательно
Обозначим 
Где 
СКО дискретной ЛС.
Таким образом КФ отклика – дискретная свертка СКФ и КФ входного воздействия.
Z форма ЭС
– знак двусторонний, 
- производная.
Z форма ЭС отклика ЛС:
Введем 
Т.к. 
.
В Частотной области 
Вопрос 3.
Найти шумовую полосу узкополосного параллельного колебательного контура
– эквивалентное сопротивление контура;
– резонансная частота; 
.
ШП 
,
- табличный интеграл для дробно
рациональной функции.
– постоянная контура.
Билет №3.
Вопрос 1.
Теорема Винера – Хинчина для непрерывных СП (доказательство первой формулы).
(Справедлива только для СП, представляющих собой пару преобразования Фурье)
Теорема Винера-Хинчина:
– КФСП; 
- ЭС.
Доказательство (1): Будем рассматривать
реализацию СП на интервале 
,
тогда
Среднее значение 
периодограммы 
запишем в виде:
Таким образом:
Область интегрирования:
Произведем замену: 
.
Область интегрирования
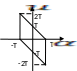
Таким образом
Откуда следует
Свойства ЭС
1. Интеграл от представляет собой среднюю мощность СП
2. Энергетический спектр вещественного СП вещественен. Учтем четность функции , тогда
3. ЭС неотрицателен. Следует из
неотрицательности 
и
придела при 
.
4. Убывает до нуля флуктуационной
составляющей 
5. ЭС четная функция частоты, т.е. 
Теорема справедлива и для взаимных КФ и ЭС:
Причем в силу свойства взаимной КФ: 
.
ВЭС 
комплексная функция даже при вещественных
СП X(t) и
Y(t). 
и 
- четные функции частоты; 
и 
- нечетные функции частоты.
Вопрос 2.
Дифференцирование СП.
Определение. Случайная функция X(t)
называется дифференцируемой в
среднеквадратическом смысле в точке
,
если существует СВ 
,
такая, что:
причем СВ
называется производной СП 
в точке
.
Теорема 1. Для дифференцируемости СП
необходимо и достаточно существование
производных
При этом
Введем обозначения 
Теорема 2. Справедливо следующее равенство для взаимной КФ исходного процесса и его производной:
Объединяя эти равенства, приходим к соотношению
Замечание. Если
- стационарный СП, когда 
,
то получим следующее соотношение:
Следовательно
Связь КФ воздействия и отклика.
Пусть 
- ИХ ЦФ. Тогда отклик ЛС
на последовательность
на входе отпредеяется дискретной
сверткой
Среднее значение отклика
Для стационарного СП
,
тогда получим 
Найдем КФ отклика
Если СП стационарное, то следовательно
Обозначим
Где СКО дискретной ЛС.
Таким образом КФ отклика – дискретная свертка СКФ и КФ входного воздействия.
Z форма ЭС
– знак двусторонний, - производная.
Z форма ЭС отклика ЛС:
Введем
Т.к. . В Частотной области