2. Понятие о разложении Карунена - Лоэва.

Ортогональное разложение СП основано на разложении КФ нестационарных СП в равномерно сходящийся ряд:

a , a

Где собственные функции, - собственные числа однородного уравнения Фредгольма второго рода:

В силу вещественности КФ, собственные функции так же вещественные. Собственные функции ортонормированные:

Любой непрерывный в среднеквадратическом смысле СП с КФ может быть разложен в ряд на [a;b]:

где

Данное ортогональное разложение называется разложением Карунена - Лоэва или каноническим разложением СП.

Найдем смешанный начальный момент первого порядка:

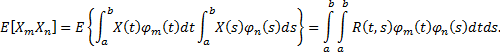
Используя уравнение Фредгольма и ортогональность собственных функций, получаем:

Таким образом, коэффициенты ряда являются некоррелированные (ортогональные) случайные величины, имеющие второй начальные момент:

3. Интегральные характеристики лс.

Непрерывные ЛС:

1)Шумовая полоса ЛС (Гц) определяется соотношением:

Где H(iω) – частотная характеристика (ЧХ) ЛС, Hm – максимальное значение АЧХ. При вычислении шумовой полосы, целесообразно пользоваться ее выражением в виде:

где табличный интеграл для дробно-рациональной функции:

где

Для системы первого порядка:

Для системы второго порядка:

2)Системная КФ (СКФ) Rh(τ) непрерывной стационарной ЛС:

- импульсная характеристика системы.

Выразим шумовую полосу через СКФ:

Получаем:

Дискретные ЛС.

СКФ цифрового фильтра:

Непрерывное время t заменяется на дискретные отсчеты n.

Системная функция -

- импульсная характеристика дискретной системы.

Формула обращения:

Выразим СКФ по формуле обращения:

Введем обозначения: k-n=m, k=l. Тогда:

Билет № 17.

Вопрос 1.

Энергетический спектр (ЭС) СП, его свойства, связь с КФ СП.

Рассмотрим реализацию некоторого процесса:

x(t)-известно

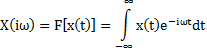
Следовательно на интервале

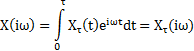
Равенство Парсеваля:

Если

Тогда: , где Э-энергия

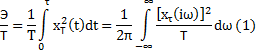
T-время ср.кв. реализации; –средн.мощность реализации

Определение. Величина наз-ся периодограммой СП

В ф.(1) перейдем к пределу: :

1)

2) – усреднение перодограммы, по (2) замечаем, что периодограмма является СВ, она меняется случайным образом от реализации к реализации .

(2)

Определение: Величина

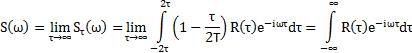
Связь ЭС и КФСП

Свойства ЭС :

1. По (2): ОВФ

2. ЭС вещественного СП является вещественной величиной

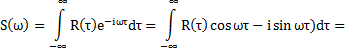
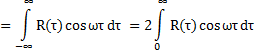
3. ЭС является неотрицательной величиной. Доказательство следует из определения ЭС и свойств периодограммы

4. Убывание до 0 флуктуационной составляющей ЭС при

5. ЭС СП - четная функция частоты

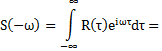
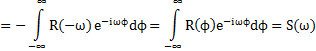
–доказано

.Найти системную КФ интегратора со сбросом.

интегратора со сбросом имеет вил

Изображение ИХ:

Очевидно, что оригиналом для этого изображения является “ступенька ” Тогда оригиналом изображения

Будет треугольный импульс

Замечание 1. Именно такой подход будет реализован и при анализе согласованного фильтра (СФ) при подаче на вход одиночного прямоугольного видеоимпульса, причем величина есть энергия такого импульса; T-длительность; A-амплитуда импульса. В этом случае сигнальный отклик равен свертке прямоугольного импульса самим с собой. Следовательно, изображение отклика линейной системы имеет вид , а сам отклик- это треугоный импульс

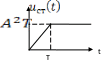
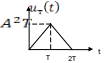
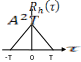
Оригинал для изображения отличается от оригинала

Сдвигом в сторону опережения. Поэтому СКФ для интегратора со сбросом принимает вид

Иногда проще вычислить сначала и затем воспользоваться стандартным переходом к