13. Теорема об улучшении несмещенных оценок с помощью достаточных статистик (теорема Блекуэлла). Утверждение об оптимальной несмещенной оценке и достаточной статистике.

Теорема 3.13 (Блекуэлл)

Пусть – несмещенная оценка , – статистика, достаточная для параметра и случайная величина является условным математическим ожиданием величины при условии :

,

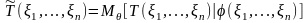тогда

1) случайная величина является статистикой;

2) ;

3) .

Доказательство:

1) Заметим, что условная случайная величина:

(3.6)

где условное распределение случайного вектора при условии . Поскольку является статистикой достаточной для параметра , то по определению, условная плотность от параметра не зависит. Таким образом, справа в (3.6) под интегралом расположены функции, которые от параметра не зависят, и следовательно интеграл является функцией только , поэтому случайная величина , является статистикой, поскольку зависит только от наблюдения :

.

2) Вычислим математическое ожидание , воспользовавшись свойством условного математического ожидания:

,

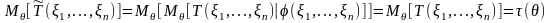поскольку является несмещенной оценкой .

3) Представим дисперсию с помощью условного математического ожидания и условной дисперсии:

.

Во втором слагаемом справа , поэтому:

,

поскольку условная дисперсия неотрицательна случайная величина, , то и математическое ожидание от неотрицательной величины условной дисперсии неотрицательно, :

.

Теорема доказана.

Утверждение 3.14.

Пусть – оптимальная оценка в классе несмещенных оценок (то есть – эффективная оценка ) и – статистика достаточная для параметра , тогда статистика является функцией :

,

где 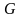некоторая функция.

Доказательство:

Определим статистику следующим образом:

,

тогда по теореме 3.13 оценка является несмещенной:

,

и кроме того,

.

Оценка является оптимальной в классе несмещенных оценок 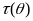, и следовательно среди всех несмещенных оценок имеет наименьшую дисперсию, поэтому для всякой несмещенной оценки, в том числе и для :

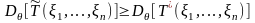
Из двух неравенств следует, что

.

Таким образом, статистика также является оптимальной оценкой в классе несмещенных оценок , но несмещенная оптимальная оценка единственна (утверждение 1.12), отсюда статистики и совпадают:

.

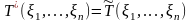Статистика является условным математическим ожиданием, и следовательно является функцией , поэтому:

.

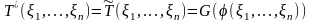Утверждение доказано.

14. Метод моментов построения точечных оценок, свойства моментных оценок.

1. Метод моментов.

Пусть – выборка из распределения , где – вектор неизвестных параметров, и требуется построить оценку величин , , …, .

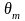Для построения оценок вычислим моментов ( ) функции распределения , в общем случае моменты могут быть как начальные, так и центральные и не обязательно по порядку. Выражения для моментов содержат неизвестные параметры , …, 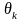, так что каждый момент представляет собой функцию :

.

Пусть представленная система разрешима относительно неизвестных параметров , …, , тогда получим систему выражений:

Точные значения моментов неизвестны, но известны оценки моментов , полученные на основе выборки . Используя оценки , получим оценки неизвестных параметров:

(4.1)

Определение 4.1.

Оценки , …, в системе (4.1) называются оценками, полученными по методу моментов (кратко, моментными оценками).

Моментные оценки , …, в общем случае не обладают свойством несмещенности (тем не менее, в некоторых частных случаях моментные оценки оказываются несмещенными).

Если функция 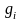( ) непрерывна в точке , то моментная оценка является состоятельной. Действительно, оценки начальных и центральных моментов являются состоятельными, откуда в силу свойства сходимости по вероятности, непрерывная функция от оценок , имеющих пределом по вероятности , сходится по вероятности к величине 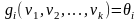, таким образом:

,

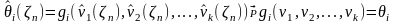что означает состоятельность оценоки .

Если в качестве используются первые начальных моментов функции распределения , функции , …, непрерывно дифференцируемы и функция распределения имеет моментов, то моментные оценки имеют асимптотически нормальное распределение:

,

где 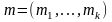– вектор начальных моментов.

Моментные оценки в большом количестве случаев не являются эффективными и оптимальными, тем не менее, метод построения оценок оказывается простым и сами выражения для моментных оценок (4.1), как правило, оказываются простыми для вычисления.

15. Метод максимального правдоподобия построения точечных оценок. Утверждения о связи между МП-оценками, эффективными оценками и достаточными статистиками. Асимптотические свойства МП-оценок: несмещенность, нормальность и эффективность.

Пусть – наблюдение (не обязательно выборка) и 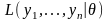– плотность вероятности (или вероятность в дискретном случае) вектора , которая зависит от неизвестного вектора параметров . В результате проведения эксперимента будет получен числовой вектор , подставляя который в функцию , получим функцию, зависящую только от вектора (функцию правдоподобия – определение 3.1). При одних значениях параметра значение функции правдоподобия оказывается мало, при других значениях – велико. Поскольку значение функция правдоподобия отражает вероятность получения заданного вектора , то волне естественно выбрать параметр так, чтобы вероятность получения наблюдаемого значения оказалось бы наибольшей.

Определение 4.2.

Пусть – наблюдение и – функция правдоподобия. Оценка , доставляющая наибольшее значение функции правдоподобия при каждом наблюдении , называется оценкой максимального правдоподобия (кратко, МП-оценкой):

.

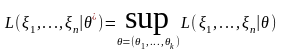Определение 4.2 следует понимать в следующем смысле: при каждом фиксированном элементарном событии , случайные величины наблюдения , …, принимают определенные числовые значения , а само наблюдение при фиксированном становится числовым вектором . Для заданного вектора согласно определению 4.2 вычисляется значение МП-оценки :

.

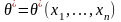Тем самым для каждого задан способ вычисления МП-оценки , который и определяет функцию наблюдения . Таким образом, МП-оценка как функция наблюдения является статистикой.

Если при каждой реализации вектора наибольшее значение функции правдоподобия соответствует внутренней точке множества допустимых значений параметра и функция правдоподобия дифференцируема по параметру, то из необходимого условия экстремума следует равенство частных производных функции правдоподобия нулю в точке МП-оценки :

, .

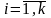Решение приведенной системы не всегда оказывается удобным, поэтому при выполнении определенных условий задачу нахождения наибольшего значения функции правдоподобия заменяют задачей нахождения наибольшего значения логарифма функции правдоподобия , поскольку логарифм функция монотонно возрастающая (и, следовательно, наибольшему значению логарифма функции правдоподобия будет соответствовать наибольшее значение самой функции правдоподобия):

, .

В случае скалярного параметра представленное уравнение имеет название уравнения правдоподобия.

Утверждение 4.3.

Пусть выполнены условия теоремы 3.4, – наблюдение и статистика является эффективной оценкой параметра , тогда является МП-оценкой параметра .

Доказательство:

Поскольку – эффективная оценка и выполнены условия теоремы 3.4, то в силу следствия 3.5 имеет место равенство:

,

.

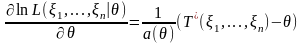Пусть – МП-оценка, тогда при всех реализациях вектора :

,

отсюда при всех реализациях векторах :

,

тогда при всех реализациях вектора :

,

.

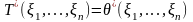Таким образом, оценки и 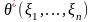совпадают.

Утверждение доказано.

Утверждение 4.4.

Пусть – наблюдение и – статистика достаточная для параметра , тогда МП-оценка параметра является функцией достаточной статистики .

Доказательство:

Поскольку – достаточная для параметра статистика, то по критерию факторизации (теорема 3.12) для функции правдоподобия имеется разложение:

В соответствии с определением МП-оценка доставляет наибольшее значение функции правдоподобия :

.

Значение параметра , соответствующее наибольшему значению функции , будет зависеть от , …, только через значения статистики , поэтому МП-оценка будет функцией статистики :

.

Утверждение доказано.

Определение 4.5.

Статистика , являющаяся оценкой неизвестного параметра , называется асимптотически эффективной, если при каждом допустимом значении :

,

где – дисперсия оценки , 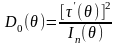– нижняя граница дисперсии из неравенства Рао-Крамера, – информация Фишера о параметре , содержащаяся в наблюдении .

Определение 4.6.

Статистика называется асимптотически нормальной с параметрами и :

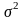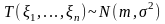при ,

если при каждом :

,

где – функция распределения , – функция Лапласа (функция распределения нормальной случайной величины с математическим ожиданием 0 и дисперсией 1).

Теорема 4.7. (асимптотические свойства МП-оценок)

Пусть – выборка из распределения с плотностью вероятностью , зависящей от скалярного параметра , – множество допустимых значений параметра, – истинное значение параметра, – МП-оценка параметра .

Если,

1) при каждом и почти всех существуют производные , 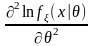и ;

2) при каждом и почти всех : и , причем существуют интегралы 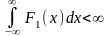и ;

3) при каждом и почти всех : и существует единая постоянная такая, что для всех : .

4) при каждом конечен и положителен интеграл:

Тогда,

1) МП-оценка состоятельна, то есть при ;

2) МП-оценка является асимптотически нормальной;

3) МП-оценка асимптотически эффективная;

16. Метод порядковых статистик: построение оценок и оценка квантилей. Понятие порядковой статистики, функция распределения и функция плотности вероятности (без доказательства) порядковых статистик. Теорема Крамера об асимптотической нормальности порядковых статистик и свойства оценок по методу порядковых статистик.

Пусть – выборка из распределения , тогда функция распределения -ой порядковой статистики :

Доказательство:

Выберем произвольным образом и зафиксируем значение , определим на основе выборки вектор бинарных случайных величин :

.

Случайные величины независимы в совокупности (поскольку случайные величины независимы в совокупности) и имеют одинаковое распределение (поскольку случайные величины имеют одинаковую функцию распределения) :

,

.

Пусть – -ая порядковая статистика, по определению функция распределения :

.

Порядковая статистика меньше величины тогда и только тогда, когда среди величин выборки ( ) величин меньше и величин не меньше , то есть тогда и только тогда, когда в векторе бинарных случайных величин величин равны 1 и величин равны 0, что эквивалентно тому, что случайная величина больше или равна . Поскольку все независимы и одинаково распределены, то случайная величина имеет распределение Бернулли с параметрами и , тогда:

(4.13)

Заметим, что полученное равенство справедливо для любого , поскольку величина была выбрана произвольным образом.

При из (4.13) получим:

.

При из (4.13) получим:

.

Утверждение доказано.

Утверждение 4.9

Пусть выполнены условия утверждения 4.8 и функция распределения дифференцируема при всех и , тогда плотность вероятности -ой порядковой статистики :

,

где – плотность вероятности.

Определение 4.10.

Пусть – функция распределения, -квантиль (квантиль уровня ) функции распределения есть число такое, что:

.

(если существует несколько значений , удовлетворяющих условию , то в качестве -квантили принимают наименьшее из этих значений).

Если распределение, соответствующее имеет название, то обычно говорят, например, «квантиль уровня нормального распределения с параметрами 0 и 1» или «квантиль уровня распределения хи-квадрат с степенями свободы».

Предположим, что функция распределения зависит от неизвестного параметра , тогда -квантиль является функцией параметра и является неизвестной величиной. Для построения оценки -квантили функцию распределения заменяют эмпирической функцией распределения .

Теорема 4.12. (Крамер)

Пусть – выборка из распределения , – -квантиль распределения и в некоторой окрестности точки плотность вероятности непрерывно дифференцируема и положительна, 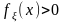, тогда статистика имеет асимптотически нормальное распределение:

, при .

Следствие

При выполнении условий теоремы 4.12 статистика 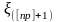является состоятельной оценкой -квантиля , поскольку математическое ожидание и дисперсия при .

Пусть функция распределения зависит от неизвестного параметра , для построения оценки величины с помощью порядковых статистик достаточно выразить величину через квантили функции распределения :

.

Использование вместо квантилей 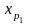, …, 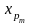их оценок, полученных с помощью порядковых статистик, , …, , приводит к статистике:

,

которая используется в качестве оценки .

При некоторых условиях статистики являются состоятельными оценками квантилей , то есть имеет место сходимость по вероятности 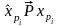при , если функция непрерывна в точке , тогда по свойству сходимости по вероятности статистика сходится по вероятности к величине :

, при ,

тогда по определению статистика является состоятельной оценкой .

Оценки, полученные методом порядковых статистик, как правило, имеют дисперсию больше, чем дисперсии оценок, полученные другими методами. Тем не менее, оценки, полученные методом порядковых статистик, могут обладать дополнительными положительными свойствами, например, устойчивостью к «засорению» выборки («засорение» выборки означает наличие в выборке ошибочных значений, полученных в результате неверного измерения и т.п.)

17. Понятие доверительного интервала, верхней и нижней доверительных границ. Понятие центральной статистики и общий метод построения доверительных интервалов с помощью центральной статистики. Метод построения центральной статистики.

Всякая точечная оценка сообщает лишь одно значение, которое принимается за приближенное значение оцениваемой величины, при этом полученное значение в большинстве случаев, конечно, не совпадает с истинным значением оцениваемой величины, поэтому в ряде случаев требуется указать интервал, в котором с большой вероятностью находится оцениваемая величина.

Пусть – наблюдение, – неизвестный скалярный параметр и – множество допустимых значений параметра .

Определение 5.1.

Пусть и – статистики. Интервал

называется доверительным интервалом для величины с уровнем доверия (доверительной вероятностью) 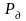( ), если:

1) ,

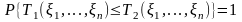2) .

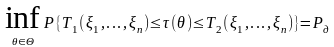Из условия 2) определения 5.1 следует, что статистики и устроены таким образом, что каким бы ни оказалось значение параметра величина «накрывается» интервалом с вероятностью не меньше чем .

Определение 5.2.

Статистика называется верхней доверительной границей с уровнем доверия (доверительной вероятностью) ( ), если:

.

Определение 5.3.

Статистика называется нижней доверительной границей с уровнем доверия (доверительной вероятностью) ( ), если:

.

Общий метод построения доверительных интервалов основывается на понятии центральной статистики.

Определение 5.4.

Пусть – наблюдение и случайная величина зависит как от наблюдения так и от неизвестной величины . Случайная величина называется центральной статистикой для величины , если:

1) функция распределения известна (то есть никаким образом не зависит от неизвестного параметра ),

2) при всех реализациях наблюдения одновременно функция непрерывна и строго монотонна по (например, при всех функция непрерывна и возрастает по ).

Предположим, что некоторым образом построена центральная статистика для – , поскольку функция распределения известна (условие 1), то всегда можно найти числа и 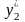такие, что:

.

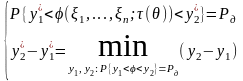Поскольку функция непрерывна по при всех реализациях наблюдения , то при каждом существуют решения и системы уравнений (рисунок 5.1):

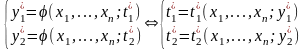
Рисунок 5.1.

Если функция возрастает по при всех реализациях наблюдения, тогда события и эквивалентны и вероятности событий равны, то есть:

.

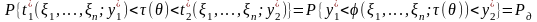Пусть статистики и , тогда интервал является доверительным интервалом для с уровнем доверия , поскольку для всех допустимых значений параметра :

,

следовательно,

.

Если функция убывает по при всех реализациях наблюдения, тогда эквивалентны события и и равны вероятности:

.

Пусть статистики и , тогда интервал является доверительным интервалом для с уровнем доверия , поскольку для всех допустимых значений параметра :

,

тогда,

Аналогичным образом, с помощью центральной статистики могут быть построены доверительные границы.