1.Основные определения математической статистики: выборка, объем выборки, реализация выборки, выборочное пространство, вариационный ряд, порядковые статистики, эмпирическая функция распределения и её свойства (теоремы о сходимости).
В теории вероятностей в качестве
формальной основы используется понятие
вероятностного пространства (
,
,
),
где
– непустое множество элементарных
событий,
–
-алгебра
множеств с единицей
,
– вероятностная мера, определенная для
множеств из
,
причем все три компоненты вероятностного
пространства считаются заданными
(определенными).
Определение 1.1.
Выборкой называется вектор случайных
величин
,
в котором:
1) все случайные величины
,
…,
независимы в совокупности,
2) все случайные величины , …, имеют одинаковую функцию распределения.
Определение 1.2.
Число
в определении выборки 1.1 называется
объемом выборки.
Определение 1.3.
Реализациями выборки называются
числовые векторы
,
такие что:
(
),
для
некоторого
.
Определение 1.4.
Выборочным пространством называется множество всех реализаций выборки,
.
Определение 1.5.
Вариационным рядом выборки
называется совокупность случайных
величин
,
,
…,
:
,
в которой принимает наименьшее из значений , …, , - наименьшее из значений , …, , следующее по величине за , и так далее, а - наибольшее из значений , …, .
Определение 1.6.
Случайные величины
,
…,
вариационного ряда называются порядковыми
статистиками. Случайная величина
называется
-ой
порядковой статистикой. Случайные
величины
и
называются экстремальными значениями
выборки.
Определение 1.7.
Эмпирической функцией распределения
называется случайная функция
:
,
где
функция
равна количеству случайных величин
выборки
меньших
.
Теорема (сходимость по вероятности)
Пусть
является эмпирической функцией
распределения, построенной по выборке
из распределения
,
тогда при всяком фиксированном
случайная величина
сходится по вероятности к
при
:
,
при
.
Теорема (равномерная сходимость по вероятности)
Пусть
является эмпирической функцией
распределения, построенной по выборке
из распределения
,
тогда последовательность случайных
величин
сходится к нулю по вероятности при
:
,
при
.
Теорема (Гливенко, сходимость с вероятностью 1)
Пусть является эмпирической функцией распределения, построенной по выборке из распределения , тогда последовательность случайных величин сходится к нулю с вероятностью 1 («почти наверное») при :
,
при
.
2. Задача точечного оценивания неизвестных величин: параметров, вероятностей и моментов. Понятие статистики и оценки, свойства оценок: несмещенность и состоятельность. Сравнение несмещенных оценок на основе дисперсий. Понятие об оптимальной оценке, утверждение о единственности оптимальной несмещенной оценки (без доказательства). Обобщение критерия сравнения оценок на основе дисперсий с использованием среднеквадратичного отклонения, функции потерь и функции условного риска.
Определение 1.8.
Статистикой называется функция наблюдения.
Общий случай постановки задачи точечного оценивания может оказаться сложным для восприятия (общий случай рассмотрен, например, в монографии [1]), поэтому рассмотрим частный, простой случай, в котором наблюдение является выборкой.
Пусть
является выборкой из распределения
,
где
– неизвестный параметр (в общем случае
вектор неизвестных параметров) из
некоторого допустимого множества
параметров
,
и требуется построить оценку неизвестной
величины
,
зависящей от параметра
.
Например, в качестве неизвестной величины
может выступать непосредственно сам
параметр
,
,
вероятность
при некотором фиксированном
,
,
или математическое ожидание
,
.
Предположим, что для оценки неизвестной
величины
некоторым образом была построена
статистика
,
являющаяся в данном случае функцией
выборки
(заметим, что оценка
является случайной величиной, как
функция случайных величин
,
…,
).
Для исследования «качества» оценки
определяют ряд свойств, среди которых
особо выделяют свойства несмещенности,
состоятельности и оптимальности.
Определение 1.9.
Оценка
является
несмещенной оценкой
,
если
:
,
где
)
и
функция распределения выборки
.
Фактически, свойство несмещенности означает, что каково бы ни было значение параметра , оценка «в среднем» окажется близкой к неизвестной величине .
Определение 1.10.
Оценка
называется состоятельной, если при
каждом
:
при
.
Из
свойства состоятельности, согласно
определению сходимости по вероятности
(приложение 1), следует, что для всяких
и
можно найти
такое, что при каждом
:
.
Фактически
это означает, что с увеличением объема
выборки
вероятность малого отклонения оценки
от значения
оказывается близкой к 1, то есть при
больших
с большой вероятностью (с вероятностью
близкой к 1), значение
окажется в
-окрестности
величины
.
Свойство состоятельности является обязательным свойством, оценки, не обладающие состоятельностью, не рассматриваются и не используются. Свойство несмещенности является желательным, более того, в некоторых случаях смещенные оценки оказываются «лучше» несмещенных, поэтому предпочтение отдают смещенным оценкам несмотря на отсутствие у них свойства несмещенности.
В некоторых случаях у оценки
существует второй центральный момент
(дисперсия)
,
который в общем случае зависит от
значения параметра
,
.
По
величине дисперсии
можно судить о мере «разброса» оценки
:
оценки с большим «разбросом» могут с
большей вероятностью принимать значения
далекие от оцениваемой величины
,
чем оценки с малым «разбросом». Кроме
того, оценка с малым «разбросом»
оказывается «сосредоточенной» вокруг
математического ожидания
,
которое в случае дополнительного
свойства несмещенности совпадает с
оцениваемой величиной
,
так что оценка фактически оказывается
«сосредоточенной» вокруг величины
.
Отсюда следует, что предпочтение следует
отдавать оценкам с малым «разбросом»
(с малой величиной дисперсии).
Используя величины дисперсий оценок, можно сформулировать критерий наименьшей дисперсии сравнения оценок – «из двух оценок лучше та оценка, у которой дисперсия меньше».
Предположим, что
есть класс несмещенных оценок величины
с ограниченной дисперсией:
:
,
.
Пусть
и
две различных оценки из класса
,
в общем случае на основе дисперсий
и
не всегда удается указать, какая оценка
«лучше», поскольку может оказаться
(рисунок 1.2), что при одном значении
параметра
:
,
а при другом
значении параметра
наоборот:
.
В этом случае по принятому критерию наименьшей дисперсии невозможно указать, какая оценка лучше.
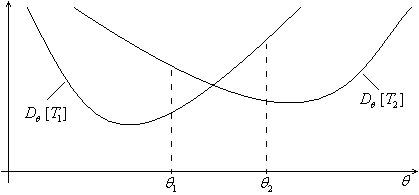
Рисунок 1.2. Дисперсии оценок.
Тем не менее, в некоторых случаях в
классе
есть оценка
,
которая при каждом значении параметра
имеет наименьшую дисперсию среди
дисперсий оценок класса
(рисунок 1.3):
:
.
В этом случае, оценка , очевидно, является наилучшей в классе и её следует признать оптимальной.
Рисунок 1.3. Дисперсия оптимальной оценки.
Определение 1.11.
Оценка
называется оптимальной в классе оценок
,
если
: .
Утверждение 1.12.
Пусть класс несмещенных оценок , если в классе существует оптимальная оценка, то она единственна.
Критерий наименьшей дисперсии не является единственным критерием сравнения оценок, для оценок общего вида, не обязательно обладающих свойством несмещенности, вводится характеристика среднеквадратической ошибки.
Определение 1.13.
Среднеквадратической ошибкой статистики , оценивающей величину , называется математическое ожидание квадрата отклонения:
.
В
случае несмещенной оценки,
,
среднеквадратическая ошибка становится
равной дисперсии, поэтому для несмещенных
оценок критерий наименьшей
среднеквадратической ошибки совпадает
с уже рассмотренным критерием наименьшей
дисперсии.
В более общем случае в рассмотрение
вводится функция потерь
,
которая используется при вычислении
функции условного риска
:
,
где
функция распределения выборки
.
Значения функции
используются для сравнения оценок, в
частности, если
,
то функция условного риска
есть среднеквадратическая ошибка.
3. Понятие состоятельной оценки и предельные теоремы, используемые для доказательства состоятельности оценок (теорема Бернулли, теорема Хинчина, неравенство Чебышева и закон больших чисел в форме Чебышева). Утверждение о состоятельности несмещенной оценки с убывающей дисперсией (без доказательства).
Теорема (Бернулли)
Пусть
– количество появлений события
в
независимых испытаниях, тогда
последовательность относительных
частот
сходится по вероятности к вероятности
события
,
при
:
,
при
.
Теорема (Хинчин)
Пусть
,
,
… – последовательность взаимно
независимых случайных величин, имеющих
одинаковую функцию распределения с
конечным математическим ожиданием
,
тогда последовательность случайных
величин
сходится по вероятности к
,
при
:
,
при
.
Утверждение (неравенство Чебышева)
Пусть случайная величина
имеет конечную дисперсию,
,
тогда:
.
Теорема (закон больших чисел в форме Чебышева)
Пусть
,
,
… – последовательность взаимно
независимых случайных величин, имеющих
конечные математические ожидания
,
,
… и конечные дисперсии
,
,
… соответственно.
Если,
,
Тогда последовательность арифметических
средних случайных величин
сходится по вероятности к арифметическому
среднему математических ожиданий
при :
,
при
.
Утверждение 2.1.
Пусть
– наблюдения, и статистика
является несмещенной оценкой величины
,
причем дисперсии
конечны и стремятся к нулю с ростом
:
,
,
,
тогда является состоятельной оценкой .
4. Задача точечного оценивания вероятности события, построение оценки и свойства оценки. Задача точечного оценивания значений функции распределения, построение оценки и свойства оценки.
Пусть выборка из распределения с неизвестным параметром , и некоторое фиксированное числовое значение, требуется построить оценку значения функции распределения – неизвестной величины (неизвестной в силу того, что параметр неизвестен) и исследовать свойства несмещенности и состоятельности построенной оценки.
Предположим, что в качестве оценки
неизвестной величины вероятности
используется значение эмпирической
функции распределения
,
,
где
согласно определению эмпирической
функции распределения 1.6 функция
равна случайной величине количества
случайных величин выборки
меньших
.
Заметим, что функцию
можно представить в виде суммы значений
индикаторных функций от случайных
величин выборки:
,
где
(
)
принимает значение 1 если
и 0 в противном случае. Таким образом,
каждая величина
является случайной величиной, принимающей
лишь два значения: 1 с вероятностью
и 0 с вероятностью
:
.
Поскольку
выборка из распределения
,
то в соответствии с определением выборки
1.1, все случайные величины имеют функцию
распределения
,
отсюда следует, что
,
Таким образом, окончательно статистика имеет вид:
|
(2.1) |
где
- случайные величины,
.
Исследуем свойства оценки (2.1), покажем, что статистика (2.1) является несмещенной оценкой , действительно, по свойству математического ожидания,
.
Для исследования свойства состоятельности оценки достаточно вспомнить теорему о сходимости по вероятности значений эмпирической функции распределения к значениям при всяком фиксированном . Поскольку оценка в точности совпадает с , то очевидно сходится по вероятности к при и, следовательно, является состоятельной.
5. Задача точечного оценивания математического ожидания и дисперсии. Понятие о выборочном среднем, выборочной дисперсии и исправленной выборочной. Несмещенность и состоятельность выборочного среднего, выборочной дисперсии и исправленной выборочной дисперсии (без вывода формулы дисперсии выборочной дисперсии).
Пусть
выборка из распределения
с неизвестным параметром
,
требуется построить оценки первого
начального момента (математического
ожидания)
и второго центрального момента (дисперсии)
(при условии, что указанные моменты
конечны):
,
и исследовать свойства построенных оценок.
Для построения оценок воспользуемся
определениями моментов, приведенными
выше, в которых неизвестную функцию
распределения
заменим известным «приближением» –
эмпирической функцией распределения
:
,
.
Поскольку
является ступенчатой функцией, с
разрывами величины
в точках
(
),
то в результате вычисления интегралов
получим следующие статистики:
|
(2.2) |
|
(2.3) |
Определение 2.2.
Статистика называется выборочным средним.
Определение 2.3.
Статистика называется выборочной дисперсией.
Легко видеть,
что оценка
является несмещенной, действительно:
.
Для доказательства состоятельности оценки может быть использована теорема Хинчина или утверждение 2.1. Заметим, что в случае использования утверждения 2.1 требуется существование дисперсий случайных величин , в то время как теорема Хинчина применима даже в тех случаях, когда у случайных величин дисперсии не существует.
В данном случае величины , , …, образуют выборку, поэтому они независимы, имеют одинаковую функцию распределения, и, следовательно, одинаковое математическое ожидание , конечность которого гарантируется исходной постановкой рассматриваемой задачи оценки. Таким образом, к совокупности случайных величин , …, при применима теорема Хинчина, и поскольку статистика есть в точности получим:
,
при
,
что и означает состоятельность оценки .
Поскольку оценка
является несмещенной, то состоятельность
оценки
может быть доказана с использованием
утверждения 2.1, при условии, что дисперсия
оценки
конечна и стремиться к нулю с ростом
.
Вычислим
непосредственно из определения статистики
:
поскольку
величины
,
…,
образуют выборку, то согласно определению
выборки они независимы в совокупности
и, следовательно, попарно независимы,
так что при
.
При
,
конечно,
,
поэтому:
|
(2.4) |
Поскольку
предполагается конечной по условию
постановки исходной задачи, приведенной
в начале пункта, то дисперсия
конечна и монотонно стремится к нулю с
ростом
,
поэтому в силу утверждения 2.1 оценка
является состоятельной.
Исследуем свойства оценки
,
предварительно преобразовав статистику
к следующему виду:
.
Вычислим
математическое ожидание
:
(поскольку
,
то
)
(дисперсия была вычислена ранее – соотношение 2.2)
Таким образом,
|
(2.5) |
и оценка оказывается смещенной, но смещение легко исправить, в результате приходим к новой оценке:
.
Оценка
является несмещенной, действительно,
.
Определение 2.4.
Статистика
называется исправленной выборочной
дисперсией.
Для доказательства состоятельности
оценки
может быть использована теорема Хинчина
и свойства сходимости по вероятности.
Ранее было получено выражение для оценки
в виде:
К
совокупности случайных величин
применима теорема Хинчина: величины
независимы
и имеют одинаковую функцию распределения
(поскольку величины
образуют выборку), кроме того, математическое
ожидание каждой величины
конечно (по условию постановки исходной
задачи, приведенной в начале пункта).
Таким образом, по теореме Хинчина:
,
при
.
Оценка является состоятельной, что по определению означает:
, при
откуда по определению сходимости по вероятности
,
при
.
Функция возведения в квадрат является непрерывной, и, как и для всякой непрерывной функции, в силу свойства сходимости по вероятности:
,
при
.
В силу свойства суммы двух пределов по вероятности,
,
при
,
откуда следует, что
,
при
,
то есть оценка в соответствии с определением является состоятельной.
Для доказательства состоятельности оценки могут быть использованы свойства сходимости по вероятности или утверждение 2.1.
В соответствии с определением оценки :
,
где
оценка
состоятельна, то есть
при
,
и числовая последовательность
стремиться к 1 при
.
Последнее означает, что для любого
всегда можно найти
такое, что при
:
,
отсюда,
считая элементы последовательности
функциями
тождественно равные постоянным, получим:
,
тогда, очевидно, что и для всякого :
.
Таким
образом, числовая последовательность
сходится по вероятности к 1 при
,
.
Оценка
,
отсюда по свойству сходимости по
вероятности:
,
при
.
Поскольку статистика
является несмещенной оценкой
,
то для проверки состоятельности
статистики
можно воспользоваться утверждением
2.1, для этого покажем, что дисперсия
статистики
конечна и стремиться к нулю с ростом
,
при
.
При вычислении дисперсии
дополнительно потребуется существование
четвертого центрального момента
:
,
будем считать, что это требование выполнено.
Прежде всего, вычислим дисперсию
статистики
,
которую, как было показано ранее, можно
представить в следующем виде:
.
Далее, подставляя выражение для получим:
.
Введем
центрированные случайные величины
,
тогда для
получим выражение:
Теперь, возводя в квадрат и преобразовывая, получим выражение:
.
Представим дисперсию в виде:
|
(2.4) |
Вычислим
:
.
Заметим,
что величины
(
)
совместно независимы, поскольку
независимы величины
(
),
так как
образуют выборку, и кроме того:
.
Рассмотрим слагаемые
в сумме
,
зафиксируем
,
и рассмотрим все возможные варианты
для индексов
и
:
1)
,
а)
– невозможно, поскольку
и
;
а)
:
;
2)
,
а) :
;
б) :
.
Таким образом,
все слагаемые
.
Рассмотрим слагаемые
в сумме
,
зафиксируем индексы
и
,
и рассмотрим все возможные варианты
для индексов
и
:
1)
:
а)
– невозможно, поскольку
и
;
б)
:
;
в)
,
:
;
2)
:
а) :
;
б) – невозможно, поскольку и ;
в) , :
;
3)
и
:
а) :
;
б) :
;
в) , :
;
Заметим, что только в случае 1б)
,
и в случае 2а)
,
слагаемое
может быть отлично от нуля, во всех
остальных случаях слагаемое
.
Таким образом, для получим выражение:
.
Поскольку , то
Поскольку
величины
(
)
независимы, то
,
тогда:
.
Таким образом,
.
Из (2.4) с учетом (2.3) получим выражение для дисперсии :
.
Зная выражение для дисперсии , легко вычислить дисперсию оценки . Поскольку , то:
.
Поскольку
и
,
то очевидно
и
,
при
,
откуда в силу утверждения 2.3 оценка
является состоятельной.