33. Неперервність функції

Означення 2.8. Функція   називається неперервною в точці   якщо:

1) вона визначена в цій точці і в деякому її околі;

2) нескінченно малому приростові аргументу відповідає нескінченно малий приріст функції:

 

, або  .                            (2.7)

 Якщо функції   і   є неперервними в точці  , тоді неперервними в цій точці будуть також функції:

 

1)  ,  ;

 

2)  ;

 

3)   за додаткової умови  .

 

Доведення. Нехай функції  ,   -неперервні в точці  . Тоді, за означенням 2.9,  ,  . Використаємо теореми про арифметичні операції над функціями, що мають границю:

 

1)  ;

 

2)  ;

 

3)  .

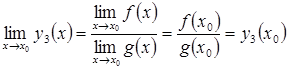Бачимо, що означення 2.9 виконується в кожному з цих випадків. Тобто ми показали, що при виконанні арифметичних дій над неперервними функціями ми знову отримаємо неперервні функції.

Точки розриву функції та їх класифікація

 Означення 2.11. Якщо функція   в точці   не є неперервною, то точка   називаєтьсяточкою розриву функції (discontinuity point).

Зауваження. Елементарна функція не може мати розривів у внутрішніх точках своєї області визначення.

 Точки розриву функції можна поділити на види:     Точки розриву першого роду .

Означення 2.12. Точка   називається точкою розриву функції   першого роду, якщо існують скінченні односторонні границі при  , але вони не рівні між собою.

 - точка розриву першого роду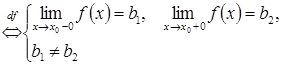 

Означення 2.13. Точка   називається точкою розриву функції   другого роду, якщо хоч би одна з односторонніх границь (зліва чи справа) при   не існує (зокрема, дорівнює нескінченності (infinite discontinuity)).

Означення 2.14. Точка   називається точкою усувного розриву функції  , якщо в цій точці виконується умова  , але або  , або   не існує. Теореми Веєрштрасса: 1)Якщо функція   неперервна на проміжку  , то вона обмежена на цьому проміжку.

2) Якщо функція   неперервна на проміжку  , то вона досягає на цьому проміжку своїх точних верхної та нижньої меж. (тобто на проміжку   знайдуться точки   та   такі, що  ,  .

34.

Функцию, имеющую конечную производную, называют дифференцируемой.

Доведення

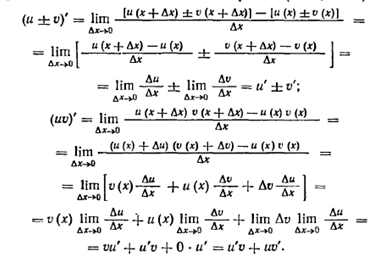
Основные правила дифференцирования:

• Если функция константа, т.е. y = C, где C - число, то (С) =0 .

• Если функции u и v дифференцируемы в точке x, то (v+u) =v +u .

• Если функция Cu , где C - постоянная, дифференцируема в точке x, то (Сu) =Сu  .

• Если функции u и v дифференцируемы в точке x, то (u v) =u v+u v .

• Если функции u и v дифференцируемы в точке x и v(x) =0, то (vu) =v2u v−u v .

36. Диференціал функції. Властивості. Інваріантність форми диференціала. Застосування до наближених обчислень. Похідні та диференціали вищих порядків. Формула Лейбніца.

Диференціалом функції f(x) називається головна лінійна частина приросту функції відносно приросту аргумента. Властивості диференціала (випливають з властивостей похідних):

1. d(u+v)=du+dv

2. d(uv)=udv+vdu

3. d(u/v)=(vdu-udv)/v²

4. dc=0, c-const

5. d(cu)=cdu

Інваріантність форми диференціала:

y = f(u(x))

y ^/ = df/dy * du/dx

dy = df/dx * dx

dy = df

Наближені обчислення: f (x + x) f (x) + f ^/(x) x

Якщо диф. похідна n-1-го порядку функції y = f(x), то похідною n-го порядку називається похідна від похідної n-1-го порядку

Позначається y⁽ⁿ⁾ , dⁿy/dxⁿ

Формула Лейбніца:

y⁽ⁿ⁾= _n^k u^(k) v^(n-k), де C_n^k = n!/k!(n-k)!