15. Мішаний добуток 3-х векторів. Означення, властивості, координатна форма(доведення). Геометричний зміст. Умова компланарності 3-х векторів.

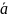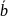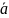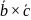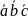Мішаним добутком вектора , вектора , вектора називається скалярний добуток ( ). Позначається , або ( ,)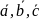

Координатна форма мішаного добутку = , = ,

=

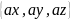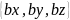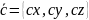
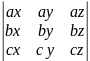
Доведення

=

= =

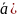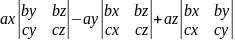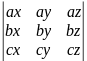
Властивості: 1.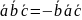 2. 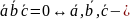компланарні 3.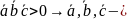 права трійка

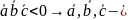ліва трійка

Вектори компланарні, якщо їх мішаний добуток дорівнює 0.

16.

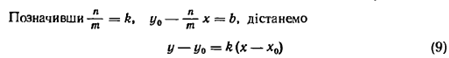
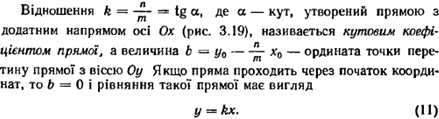
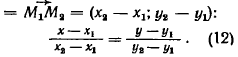
17.Рівняння прямої у відрізках на осях.Рівняння прямої з кутовим коефіцієнтом Рівняння прямої в відрізках на осях

Якщо пряма перетинає вісі OX і OY в точках з координатами (a, 0) і (0, b), то вона може бути знайдена, якщо використати формулу рівняння прямої в відрізках

x	+	y	= 1
a		b

Рівняння прямої з кутовим коефіцієнтом

Загальне рівняння прямої коли B≠0 можна привести к вигляду

y= k x+ b

де k - кутовий коефіцієнт, який дорівнює тангенсу кута, утвореного даною прямою і додатним напрямком осі ОХ

Нормальне рівняння прямої: , при цьому p – довжина перпендикуляра, який опущено з початку координат на пряму,  – кут, який цей перпендикуляр утворює з додатнім напрямком осі Ox, (рис. 16).

18.Нормальне рівняння прямої, відстань від точки до прямої (доведення)

Теорема 1. Відстань від точки   до прямої  : , (дрис. 1) обчислюється за формулою  (1) Доведення. Припустимо, що точка   є проекцією точки   на пряму ( ).  Тоді вектор  колінеарний нормальному вектору прямої ( )  . Враховуючи це, одержимо з однієї сторони   а з іншої сторони  де 

Звідки випливає   а оскільки   і   може приймати значення 0, або  , то остаточно одержуємо .

19. Угол между двумя прямыми, условия паралелльности перпендикуляр. Двух прямих

1.Угол между двумя прямыми

Угол между двумя прямыми равен углу между их направляющими векторами. Таким образом, если вам удастся найти координаты направляющих векторов a = (x₁; y₁; z₁) и b = (x₂; y₂; z₂), то сможете найти угол. Точнее, косинус угла по формуле:

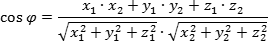
Если уравнения прямой заданы в общем виде A₁x + B₁y + C₁ = 0, A₂x + B₂y + C₂ = 0,        

угол между ними определяется по формуле      

2. Условия параллельности двух прямых:

а) Если прямые заданы уравнениями с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов: k₁ = k₂.    

б) Для случая, когда прямые заданы уравнениями в общем виде, необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

3. Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

    

21.Відстань від точки до площини.

d =	|A·Mx + B·My + C·Mz + D|
	(A2 + B2 + C2)1/2

Відстань від точки до площини — дорівнює довжині перпендикуляра, опущеного з точки на площину. Якщо задано рівняння площини Ax + By + Cz + D = 0, то відстань від точки M(M_x, M_y, M_z) до площини можна знайти використовуючи наступну формулу