10.Лінійна залежність і невизначеність векторів.Базис на площині і в просторі. Тами

11. Проекція вектора на вісь

Віссю називається пряма, на якій вибрано додатний напрям і одиниця довжини. Вісь цілком визначається одиничним вектором (ортом).

Проекцією точки М на задану вісь називається основа перпендикуляра, опущеного з даної точки М на задану вісь. Проекцією вектора   на вісь називається довжина вектора  , розміщеного між проекціями початку та кінця вектора  , причому ця довжина береться з додатним знаком, коли вектор   має напрям орта вісі, та з від’ємним – коли  і орт вісі мають протилежні напрями. Проекція вектора на вісь є скаляр.

Проекція вектора   на вісь   дорівнює добутку довжини цього вектора на косинус к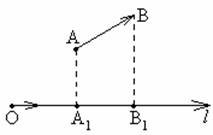 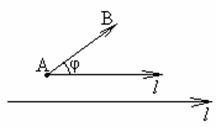ута  між вектором і віссю  :

Пр  

12. Вектори в пдск

Вектор — величина, яка характеризується числовим значенням і напрямком.

А (а₁;а₂;а₃), В(b₁;b₂;b₃) тоді АВ^→ = {b₁–а₁; b₂–а₂; b₃–а₃}

|ā| = √(а₁²+а₂²+а₃²)

ṝ = {r_x; r_y; r_z}

r_x= пр_Ox ṝ = пр_i ṝ = |ṝ|cosα r_y = пр_Oy ṝ = пр_jṝ = |ṝ|cosβ r_z = пр_Oz ṝ = пр_kṝ = |ṝ|cosγ

ē = { cosα; cosβ; cosγ } – орт (координатами орта є напрямні косинуси)

В ПДСК АВ^→ = {x_B–x_A; y_B–y_A; z_B–z_A}

Поділ відрізка у даному відношення

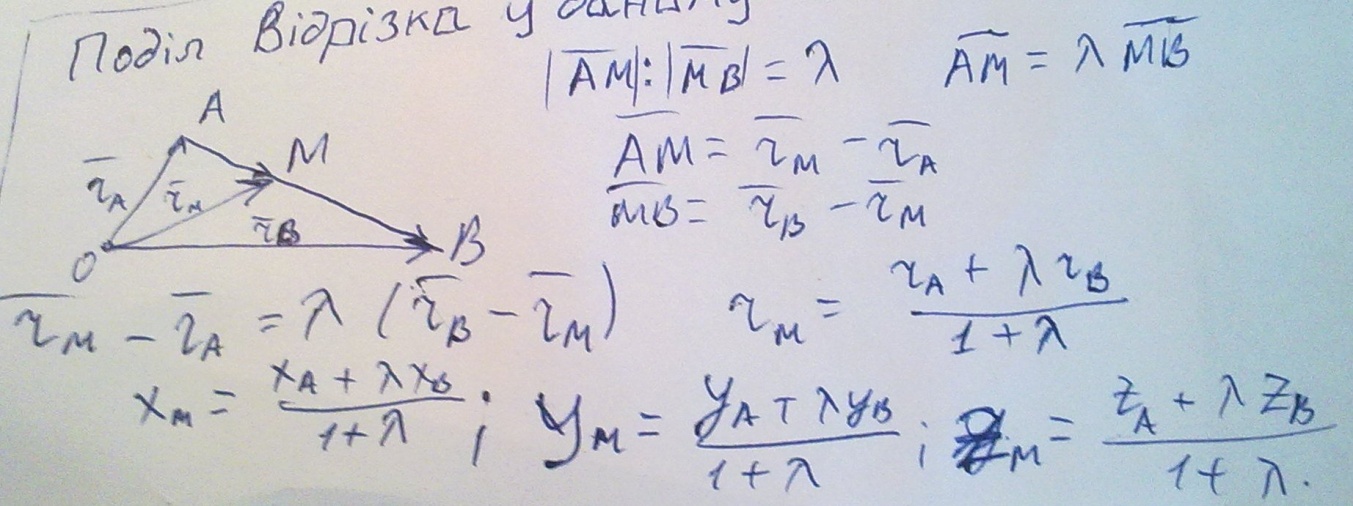
13. Скалярний добуток

Скалярний добуток — математична операція над двома векторами, результатом якої є скаляр. Скалярний добуток векторів та обчислюється за формулою:

Вираз скалярного добутку через координати векторів та обчислення кута між векторами.

Нехай вектори  а  і b   задані своїми координатами

Тоді                             (5.4)

Справді,

оскільки   ,   ,    та   .

1)   умова перпендикулярності векторів   a  і b  :  ;

Геометричний зміст скалярного добутку.

Скалярний добуток двох векторів дорівнює добутку довжини одного вектора на проекцію на нього другого вектора.

14.Векторний добуток.Означееня,властивості,координатна форма (доведення)

Найчастіше для позначення векторного добутку вживається символ ×. Векторний добуток позначається також квадратними дужками, в яких співмножники розділені комами.

Алгебраїчне означення векторного добутку

Довільний вектор в   описується своїми координатами відносно стандартного базису   Векторним добутком двох , -векторів

називається  -вектор

який також символічно записується у вигляді   детермінанту:

.

Насправді ці формули для векторного добутку виконуються у будь-якому ортонормальному базисі  .

Геометричне означення векторного добутку

Векторний добуток (вертикально) змінюється разом з кутом між векторами.

Векторним добутком двох  -векторів   називається  -вектор  , який задовольняє наступним вимогам:

1.  де   —це кут між 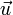  та 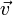  (довжина або правило паралелограму);

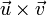2. вектор   — ортогональний до векторів   та   (ортогональність);

3. вектори   утворюють праву трійку векторів (орієнтація).

Праві та ліві трійки векторів

Два упорядковані базиси(або лінійно-незалежні трійкивекторів) називаються еквівалентними, якщо існує неперервна деформація першого у другий (із збіганням порядку векторів базису), яка складається виключно з базисів (або лінійно-незалежних трійок векторів)   Тоді всі лінійно-незалежні трійки векторів   поділяються на два класи еквівалентності, що називаються лівими таправими трійками (базисами).

Праву (ліву) трійки векторів можна наочно уявити так. Після суміщення початків, вектори правої (лівої) трійка розташуються так як великий, незігнутий вказівний та середній пальці правої (лівої) руки.

Властивості векторного добутку

Антикомутативність:

Білінійність: Тотожність Якобі:

На відміну від переважної більшості бінарних операцій "добутку" (дійсних чи комплексних чисел, елементів групи тощо), векторний добуток не є асоціативним.

Правило паралелограму:Довжина векторного добутку двох векторів чисельно дорівнює площі паралелограму який побудований на векторах-співмножниках відкладених від спільної точки.

Як наслідок з попередньої властивості, векторний добуток дорівнює нулю тоді і тільки тоді, коли співмножники — паралельні (тобто скалярно пропорціональні), зокрема, векторний добуток будь-якого вектору на себе — нульовий вектор.

Матриця векторного добутку

Векторний добуток може бути записаним як добуток косо-симетричної матриці та вектора:

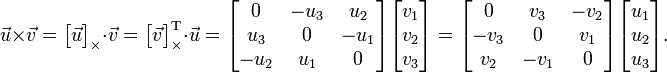
Властивість 1. Модуль векторного добутку двох векторів a і b дорівнює площині паралелограма побудованого на цих векторах.

Властивість 2. Якщо векторний добуток двох векторів a і b дорівнює нулю то вектори колінеарні.