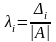1.Доведення:коли міняємо місцями рядок і стовпчик ,то визначник не міняється ,за основною властивістю просто розкриваємо 2 визначники і переконуємось ,що вони рівні,от і все.

2.

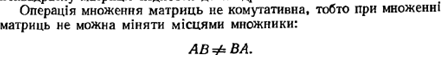
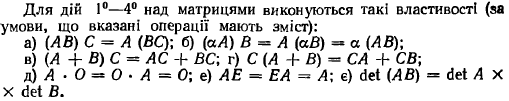
ВИДИ

1.Одинична матриця — квадратна матриця розміру n з одиницями на головній діагоналі та нулями у всіх інших елементах.

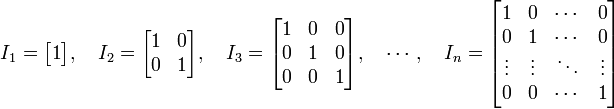
• Квадратна матриця в нульовому степені дає одиничну матрицю того ж розміру:

• Добуток невиродженої квадратної матриці на обернену матрицю дає одиничну матр.

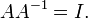
• Оберненою до одиничної матриці є вона сама:

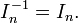
• Множення довільної матриці на одиничну відповідної розмірності дає в результаті ту ж саму матрицю, тобто вона є нейтральним елементом для множення матриць:

2. нульова матриця — матриця всі елементи якої рівні нулю. Приклади нульових матриць:

Нульова матриця є матрицею лінійного перетворення, що переводить довільний вектор у нульовий вектор.

3.Діагональна матриця — квадратна матриця, всі недіагональні елементи якої дорівнюють нулю.

Властивості:Сума, добуток та обернена матриця(якщо існує) діагональних матриць є діагональною матрицею. Визначник діагональної матриці дорівнює добутку всіх елементів головної діагоналі.

4.Квадратною матрицею порядку n називається матриця, яка має n рядків та n стовпчиків.

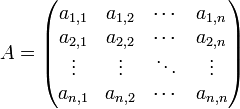.Система лінійних алгебраїчних рівнянь із невиродженою квадратною матрицею має єдиний розв'язок. Якщо стовпець правої частини нульовий, то система має тільки нульовий розв'язок.

5.Операція множення двох матриць вводиться лише для узгоджених матриць. Матриця А називається узгодженою з матрицею В, якщо кількість стовпців першої матриці А дорівнює кількості рядків другої матриці В.

6.Ви́роджена ма́триця — квадратна матриця, визначник якої дорівнює нулю:

Властивості: матриці менший за розмірність матриці.У виродженої матриці немає оберненої матриці.Матриця є виродженою тоді і тільки тоді якщо серед її власних значень є нулі.

7.Неви́роджена ма́триця — квадратна матриця, визначник якої не дорівнює нулю:

Властивості: матриці дорівнює розмірності матриці.У невиродженої матриці є обернена матриця.Матриця є невиродженою тоді і тільки тоді якщо всі її власні значення є ненульовими.

3. Обернена матриця

Обернена матриця — матриця (позначається А^-1), яка існує для кожної невиродженої квадратної матриці А, розмірності nxn , причому:

A А^-1 = А^-1A = E_n,

де E_n – одинична матриця.

detA*detA^-1 = 1; detA^-1 = 1/detA

Умова існування: якщо матриця А невироджена, то вона має обернену матрицю А^-1.

Квадратна матриця наз. невиродженою, якщо її визначник не дорівнює нулю (detA ≠0); якщо detA=0, то А – вироджена матриця.

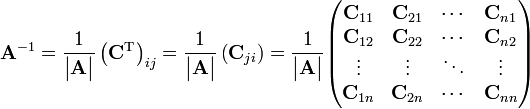
тут |A| = detA, a C_ij=A_ij – це алгебраїчне доповнення.

Доведення можна подати у вигляді добутку матриці загального вигляду 2х2 на її обернену матрицю, якщо помножите все правильно то вийде одинична матриця з одиничками в головній діагоналі й нуликами в іншій.

4.Ранг матриці і його властивості, способи знаходження рангу

Нехай задано матрицю Аmхn= А. Виділимо в матриці А будь-які k рядків і стільки ж стовпців, де k — число, не більше чисел m і n, тоб­то k  min (m, n).

Визначник порядку k, складений з елементів, що стоять на перети­ні виділених рядків і стовпців, називається мінором k-го порядку мат­риці А.

Рангом r (А) матриці А називається найбільший з порядків ЇЇ мі­нор ів, відмінних від нуля.

1) Ранг існує для будь-якої матриці Аmхn, причому 0 r (A) min(m, n);

2) r (А) = 0 тоді і тільки тоді, коли А = 0;

3) для квадратної матриці n-го порядку ранг дорівнює n тоді і тіль­ки тоді, коли матриця невироджена.

Ранг матриці можна знайти так. Якщо всі мінори першого порядку (елементи матриці) дорівнюють нулю, то r = 0. Якщо хоч один з мінорів першого порядку відмінний від нуля, а всі мінори другого по­рядку дорівнюють нулю, то r = 1.У випадку, коли є мінор другого по­рядку, відмінний від нуля, досліджуємо мінори третього порядку. Так продовжуємо доти, поки не станеться одне з двох: або всі мінори по­рядку k дорівнюють нулю, або мінорів порядку k не існує, тоді r = k – 1.

Приклад:Знайти ранг матриці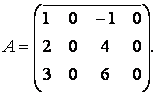

Серед мінорів першого порядку (тобто елементів матриці) є відмінні від нуля) тому r (А)  1.

Оскільки один з мінорів другого порядку

а всі мінори третього порядку дорівнюють нулю, то r (А) = 2. •

Вказаний метод знаходження рангу матриці не завжди зручний, тому що пов'язаний з обчисленням значного числа визначників. Про­стіший метод грунтується на тому, що ранг матриці не змінюється, якщо над матрицею виконати так звані елементарні перетворення, а саме: а) переставити місцями два рядки (стовпці);

б) помножити кожен елемент рядка (стовпця) на один і той самий відмінний від нуля множник;

в) додати до елементів рядка (стовпця) відповідні елементи друго­го рядка (стовпця), помножені на одне і те саме число.

5 Питання Системи лінійних алгебраїчних рівнянь

Def.    Систему m рівнянь з n невідомими вигляду

називають системою лінійних алгебраїчних рівнянь (СЛАР). Тут x 1 , x 2 , …, x n – невідомі; a ij – задані коефіцієнти (i=1, 2, …, m,  j=1, 2, …, n); b 1 ,b 2 , …, b n – вільні члени системи.

Розв’язати систему (3.1) – значить знайти такі значення невідомих     …,    при підстановці яких у систему усі її рівняння обертаються у тотожність.

СЛАР називають однорідною, якщо всі вільні члени рівні нулю, і неоднорідною, якщо хоч один з них не дорівнює нулю. Однорідна система завжди має нульовий (тривіальний) розв’язок. 

Систему рівнянь називають сумісною, якщо вона має хоча б один розв’язок, і несумісною, якщо вона не має жодного розв’язку.

Сумісну систему називають визначеною, якщо вона має один-єдиний розв’язок і невизначеною, якщо вона має більше одного розв’язку.

Матричний метод рішення (метод вирішення через обернену матрицю) систем лінійних алгебраїчних рівнянь з ненульовим визначником полягає в наступному.

Нехай дана система лінійних рівнянь з   невідомими (над довільним полем):

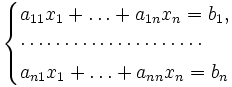
Тоді її можна переписати в матричній формі:  , Де   - Основна матриця системи,   і   - Стовпці вільних членів і рішень системи відповідно:

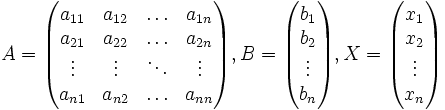
Помножимо це матричне рівняння зліва на   - Матрицю, зворотну до матриці  : 

Так як   , Отримуємо   . Права частина цього рівняння дасть стовпець рішень вихідної системи. Умовою застосовності даного метод є невироджених матриці A. Необхідною і достатньою умовою цього є нерівність нулю визначника матриці A:  .

Алгоритм рішення СЛАУ методом Гауса підрозділяється на два етапи.

• На першому етапі здійснюється так званий прямий хід, коли шляхом елементарних перетворень над рядками систему призводять до ступінчастою або трикутній формі, або встановлюють, що система несумісна. А саме, серед елементів першого стовпця матриці вибирають ненульовий, переміщують його на крайнє верхнє положення і за допомогою арифметичних дій під головною діагоналлю робимо нулі(тобто стає трапецієвидною).

• На другому етапі потрібно всі отримані базисні змінні через небазисних і побудувати систему рішень, або, якщо всі змінні є базисними, то виразити в чисельному вигляді єдине рішення системи лінійних рівнянь. Ця процедура починається з останнього рівняння, з якого висловлюють відповідну базисну змінну (а вона там всього одна) і підставляють в попередні рівняння, і так далі, піднімаючись по "сходинках" наверх. Кожному рядку відповідає рівно одна базисна змінна, тому на кожному кроці, крім останнього (самого верхнього), ситуація в точності повторює випадок останнього рядка.

Правило Крамера розв’язування визначених систем лінійних рівнянь з n рівнянь та n невідомих.

Застосовується тільки для визначених систем з n рівнянь та n невідомих !!!

Нехай маємо систему з n рівнянь та n невідомих.

(1)

Нехай А – основна матриця системи (1) і Припустимо спочатку, що система (1) сумісна і одним з розв’язків є Отже, справедливі рівності

(2)

Помножимо обидві частини рівностей з системи (2) на алгебраїчні доповнення першого стовпчика матриці А: першої на , другої на 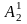і т.д. і додамо окремо ліві і праві частини рівностей.

Одержимо:

За властивостями 9-11 маємо:

, або , де через 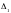позначено визначник, одержаний з визначника матриці А заміною першого стовпчика на стовпчик вільних членів.

Аналогічно де 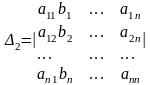і т.д.

Отже, якщо розв’язок існує, то він є єдиним і задається формулами: