1)Уравнение прямой, проходящей через две различные точки на плоскости

Если прямая проходит через две точки A(x₁, y₁) и B(x₂, y₂), такие что x₁ ≠ x₂ и y₁ ≠ y₂ то уравнение прямой можно найти, используя следующую формулу:

x-x1	=	y-y1
x2-x1		y2-y1

Параметрическое уравнение прямой в пространстве

П араметрические уравнения прямой могут быть записаны следующим образом x=lt+x0 y=mt+y0 z=nt+z0

где (x₀, y₀, z₀) - координаты точки лежащей на прямой, {l; m; n} - координаты направляющего вектора прямой.

2)Условие перпендикулярности и параллельности прямых на плоскости

Прямые y=k₁x+b₁ и y=k₂x+b₂ перпендикулярны ↔ k₁k₂= -1

Прямые y=k₁x+b₁ и y=k₂x+b₂ параллельны ↔ k₁=k₂

Билет №9. Окружность и ее уравнение. Определение эллипса и его каноническое уравнение.

1. Окружность – замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра), лежащей в той же плоскости, что и кривая.Уравнение окружности ω (A; R) имеет вид (x – a)² + (y – b)² = R², где a и b – координаты центра A окружности ω (A; R) .

Доказательство:

Пусть задана окружность ω (A; R) на плоскости Oxy, где точка A, центр окружности – имеет координаты a и b. По определению окружности для любой точки B (x; y), лежащей на окружности ω (A; R), верно AB = R. Но в соответствии с теоремой (Если A₁ (x₁; y₁), A₂ (x₂; y₂) две произвольные точки плоскости Oxy, а d – расстояние между ними, то d вычисляется из соотношения d² = (x₁ – x₂)² + (y₁ – y₂)²)AB² = (x – a)² + (y – b)². Таким образом, координаты x и y любой точки окружности ω (A; R) удовлетворяют уравнению (x – a)² + (y – b)² = R².

Обратно: любая точка B (x; y), координаты которой удовлетворяют уравнению, принадлежит окружности, так как расстояние от нее до точки A (a; b) равно R. Отсюда по определению данное уравнение – уравнение окружности ω (A; R).

2. Эллипс – множество всех точек плоскости, для которых сумма расстояний от двух данных точек, называемых фокусом, есть величина постоянная, большая, чем расстояние между фокусами.

Пусть сумма расстояний от точки эллипса до фокусов равна 2а, а расстояние между фокусами – 2с. Тогда в выбранной системе координат эллипс имеет уравнение (каноническое уравнение):

Где

Билет №10. Определение гиперболы и ее каноническое уравнение.

Гипербола – это множество всех точек на плоскости, для которых модуль разности расстояний от двух данных точек, называемых фокусами, есть величина постоянная, меньшая, чем расстояние между фокусами.

Пусть расстояние между фокусами F₁ и F₂ гиперболы равно 2c, а абсолютная величина разности расстояний от точки гиперболы до фокусов равна 2a. Тогда гипербола в выбранной выше системе координат имеет уравнение (каноническое уравнение):

Где

Билет №11. Определение параболы и ее каноническое уравнение.

Парабола – это множество всех точек плоскости, каждая из которых находится на одинаковом расстоянии от данной точки, называемой фокусом, и от данной прямой, называемой директрисой и не проходящей через фокус.

Парабола – это геометрическое место точек, равноудаленных от данной прямой (называемой директрисой параболы) и данной точки ( называемой фокусом параболы)

     Каноническое уравнение: y² =2px

Где  p>0 — параметр параболы

Билет №12. Матрицы и основные определения, связанные с этим понятием (квадратная матрица, прямоугольная матрица, треугольная матрица, трапецеидальная матрица, диагональная матрица, единичная матрица, нулевая матрица, транспонированная матрица, скалярная матрица). Действия с матрицами (сложение, умножение на скаляр, перемножение матриц, транспонирование матриц). Законы, которым эти действия удовлетворяют.

Матрица (mxn) – прямоугольная таблица чисел, в каждой клетке которой находится число, однозначно определяемое его местоположение. (Матрицей называется прямоугольная таблица из чисел, содержащая некоторое количество m строк и некоторое количество n столбцов.)

Квадратная матрица – это матрица, которая имеет одинаковое количество строк и стольцов, т.е. m=n.

Прямоугольная матрица – это ОБЫЧНАЯ МАТРИЦА!!!!!!!! (НЕ НАШЛА НИГДЕ ОПРЕДЕЛЕНИЯ!)

Треугольная матрица – Квадратная матрица, все элементы которой выше или ниже главной диагонали равны нулю. (2 вида треугольной матрицы: верхняя треугольная и нижняя треугольная).

Трапецеидальная (ступенчатая) матрица – прямоугольная матрица, которую можно разделить вертикальной чертой так, что слева получится треугольная матрица, а справа – прямоугольная.

Диагональная (скалярная матрица) – матрица, все элементы которой, кроме элементов главной диагонали, равны нулю.

Единичная матрица – это матрица, элементы главной диагонали которой равны 1, а все остальные – нулю.

Нулевая матрица – матрица, все элементы которой равны нулю.

Матрица А является транспонированной по отношению к матрице В, если столбцы матрицы А являются строками матрицы В.

Действия с матрицами:

1. Сложение:

Суммой двух матриц одинакового размера называется матрица такого же размера, каждый элемент которой равен сумме соответствующих элементов слагаемых.

A + B = C <=> c_ij=a_ij + b_ij

Свойства сложения:

А + В = В + А

(А + В) + С = А + (В + С)

А + 0 = А

А + (-А) = 0

2. Разность:

Разностью двух матриц одинакового размера называется матрица того же размера, каждый элемент которой равен разности соответствующих элементов данных матриц.

А – В = А + (-В) = С <=> c_ij=a_ij - b_ij

3. Умножение матрицы на скаляр:

Произведением матрицы на число называется матрица того же размера, каждый элемент которой равен произведению соответствующего элемента данной матрицы на это число.

а*В=С <=> c_ij=a*b_ij

Свойства:

1 * А = А, (-1) * А = -А

a*(bA)=(ab)A

a(A+B)=aA+aB

(a+b)A=aA+bA

4. Умножение матриц.

Умножением матрицы размера mXn на матрицу размера nxk называется матрица размера mxk, элементы которой, стоящие на пересечении i-ой строки и j-ого столбца, равен сумме произведений соответствующих элементов i-ой строки на элементы j-ого столбца.

Свойства:

AE = EA = A

A = 0a = 0

(AB)C = A(BC)

a(AB) = (aA)B = A(aB)

(A+B)C = AC + BC

C (A + B) + CA + CB

A⁰=E; A¹=A; при k>1 A^k = A * A^k-1 = A^k-1 * A/

Если А и В – квадратные матрицы одного и того же порядка, причем AB=BA, то

(A+B)²=A²+2AB+B²

(A-B)²=A²-2AB+B²

(A-B)(A+B) = A²-B²

Транспонирование матриц:

Транспонированной по отношению к матрице А называется матрица А^Т, столбцы которой являются строками матрицы А с теми же номерами.

Билет №13. Определения определителя и его свойства. Определитель, минор и алгебраическое дополнение элемента определителя. Вычисление определителя произвольного порядка.

Определитель матрицы – это число, которое сопоставляется квадратной матрице по определенному закону. (обозначается II либо det)

Свойства:

1. Det (AB) = det A * det B

2. Det A = det A^Т

3. Det A^-1=1/detA

4. Если все элементы какой-либо строки или столбца определителя равны нулю, то определитель тоже равен нулю.

5. Если матрица В получена из матрица А перестановкой каких-либо 2ух строк или столбцов, то debt = -detA.

6. Общий множитель всех элементов любой строки или столбца можно выносить за знак определителя.

7. Определитель, содержащий 2 пропорциональные строки или столбца, равен нулю.

8. Определитель не меняется от прибавления к какой-либо строке (столбцу) другой строки (столбца), умноженной(ого) на произвольное число.

9. Если какая-либо строка (столбец) есть линейная комбинация другой строки (столбца), то такой определитель равен нулю.

Минором (M_ij) называется определитель, полученный из исходной матрицы вычеркиванием строки и столбца на пересечении которых стоит элемент a_ij.

Алгебраическим дополнением элемента a_ij матрицы А называется минор, умноженный на (-1)^i+j

Определителем матрицы второго порядка называется число, равное разности между произведением элементов главной диагонали и произведением элементов побочной диагонали.

Определитель матрицы n-ого порядка вычисляется путем разложения строки или столбца.

Билет №14. Обратная матрица. Способы вычисления обратной матрицы.

Матрица А является обратной матрицей матрице В, если выполняется равенство: АВ=ВА=Е. Из определения следует, что В будет квадратной матрицей того же порядка что и матрица А (иначе одно из произведений АВ или ВА было бы не определено).

Существую несколько способов нахождения обратной матрицы. Один из них – нахождение обратной матрицы путём вычисления алгебраических дополнений. Заключается он в следующем:

пусть нам дана матрица А, имеющая следующий вид:

Предположим, что DА¹0. Построим следующую матрицу С следующим образом:

где А_ij – алгебраическое дополнение элемента а_ij в определителе матрицы А. Очевидно, что для построения матрицы С необходимо сначала заменить элементы матрицы А соответствующими им алгебраическими дополнениями, а затем полученную матрицу транспонировать.

Полученная таким образом матрица С называется присоединённой к матрице А, или союзной с А.

Чтобы получить матрицу А^-1, обратную для матрицы А, необходимо каждый элемент присоединённой матрицы С поделить на DА, т.е. матрица А^-1 будет иметь следующий вид:

Пусть матрица А, имеет следующий вид:

Чтобы найти матрицу А^-1, обратную для матрицы А, необходимо:

• вычислить определитель матрицы (DА= -3);

• найти алгебраические дополнения элементов а_ij в определителе матрицы А:

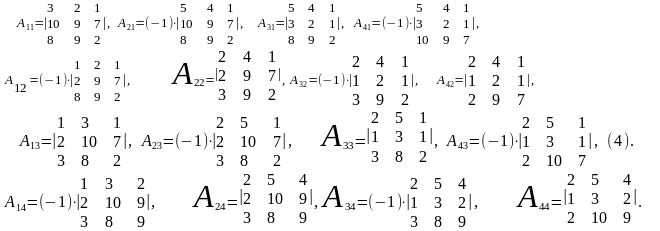
• составить присоединённую матрицу С по формуле (2);

• разделить все элементы матрицы С на DА.