
- •Формулы, связывающие координаты точки в этих системах:
- •Разложение произвольного вектора по ортам координатных осей в пространстве (на плоскости аналагично):
- •1)Уравнение прямой, проходящей через две различные точки на плоскости
- •Параметрическое уравнение прямой в пространстве
- •2Ой способ (не нашла его, поэтому своими словами!!):
- •2)Метод Крамера
Билет №1. Понятие геометрического вектора. Основные определения, связанные с этим понятием (длина вектора, равенство векторов, нуль-вектор, коллинеарные и компланарные векторы, орт вектора). Линейные операции с геометрическими векторами. Законы, которым удовлетворяют эти операции. Разность векторов. Коллинеарные векторы.
Геометрический вектор – это направленный отрезок прямой, т. е. отрезок, один из концов которого является началом, а другой – концом.
Длина вектора АВ – это длина отрезка АВ. (Расстояние между началом и концом вектора называется его длиной или модулем). (обозначается модулем).
Равенство векторов. Векторы a и b равны, если они коллинеарные, одинаково направленные и имеют одинаковые длины. (2 вектора равны, если координаты, имеющие один и тот же номер, равны.)
Нуль-вектор – двухмерный вектор, координаты которого равны нулю. (Двухмерный вектор – упорядоченная пара чисел.) Вектор, у которого начало совпадает с концом.
Векторы
a
и b
коллинеарные, если они лежат на одной
прямой или на параллельных прямых. Любые
два вектора
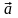 и
и
 коллинеарны, если связаны соотношением
коллинеарны, если связаны соотношением
 ,
где
,
где
 - некоторое число.
- некоторое число.
Три вектора (или большее число) называются компланарными, если они, будучи приведенными к общему началу, лежат в одной плоскости.
Орт вектор – это единичный вектор, т. е. вектор, длина которого равна 1.
Линейные операции – это сложение и вычитание векторов, а также умножение вектора на число:
Сложение свободных векторов.
Суммой двух свободных векторов, таких, что начало вектора b приложено к вектору a, называется вектор с=a+b, который соединяет начало вектора a и конец вектора b.
Суммой двух свободных векторов, присоединенных к одному началу, называется вектор с, имеющий общее начало с векторами a и b и совпадают с диагональю параллелограмма, построенного на этих векторах.
Разность свободных векторов.
Умножение вектора на число. Произведением вектора на число называется вектор , определенный следующими условиями:

Вектор b коллинеарен вектору a
Векторы a и b одинаково направлены, если >0, и противоположно, если <0.
Разностью
двух векторов
и
называется такой вектор
 ,
сумма которого с вычитаемым
дает вектор
.
Значит, если
,
сумма которого с вычитаемым
дает вектор
.
Значит, если
 ,
то
,
то
 .
.
Свойства линейных операций:
+ = +
(a + b) + c = a + (b + c)
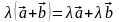


+ 0 =
+ (- ) = 0
1 * =
Билет №2. Декартова и полярная системы координат на плоскости. Формулы, связывающие координаты точки в этих системах. Декартова система координат в пространстве. Деление отрезка в заданном соотношении.
Декартовая система координат – прямоугольная система координат. Две взаимно перпендикулярные оси Ох и Оу, имеющие общее начало О и одинаковую масштабную единицу, образуют прямоугольную систему координат на плоскости.
Полярная система координат состоит из некоторой точки О, называемой полюсом, и исходящего из него луча ОЕ – полярной оси. Кроме того, задается единица масштаба для измерения длин отрезков. Полярная система координат ставит соответствие каждой точке плоскости пару чисел (Ро и фи) –> А (Ро; Фи).
Формулы, связывающие координаты точки в этих системах:
Пару
полярных координат r и
![]() можно перевести в Декартовы координаты
x и y путём применения тригонометрических
функций синуса и косинуса:
можно перевести в Декартовы координаты
x и y путём применения тригонометрических
функций синуса и косинуса:
x = rcos φ,
y = rsin φ,
в то время как две декартовы координаты x и y могут быть переведены в полярную координату r:
r2 = y2 + x2 (по теореме Пифагора).
Для определения угловой координаты следует принять во внимание два следующие соображения:
Для
![]() ,
может быть произвольным действительным
числом.
,
может быть произвольным действительным
числом.
Для
![]() , чтобы получить уникальное значение
, следует ограничиться интервалом в 2π.
Обычно выбирают интервал
, чтобы получить уникальное значение
, следует ограничиться интервалом в 2π.
Обычно выбирают интервал
![]() или
или
![]() .
.
Для вычисления в интервале , можно воспользоваться такими уравнениями (arctg обозначает обратную функцию к тангенсу):

Для вычисления в интервале , можно воспользоваться такими уравнениями:

Прямоугольная (декартова) система координат в пространстве образуется тремя взаимно перпендикулярными осями координат OX, OY и OZ. Оси координат пересекаются в точке O, которая называется началом координат, на каждой оси выбрано положительное направление, указанное стрелками, и единица измерения отрезков на осях. Единицы измерения обычно одинаковы для всех осей (что не является обязательным). OX — ось абсцисс, OY — ось ординат, OZ — ось аппликат.
Билет №3.Деление отрезка в заданном соотношении.
Дан произвольный отрезок M1M2 и М- любая точка этого отрезка, отличная от точки М2.
Число λ- отношение, в котором точка М делит отрезок М1М2.
λ= М1М \ ММ2
Теорема:
Если точка М(x, y) делит отрезок M1M2 в отношении λ, то координаты этой точки определяются формулами:
X= x1+ λx2 \ 1+ λ
Y= y1+λy2 \ 1+λ
где x1, y1 - координаты точки М1,
x2, y2 - координаты точки М2 .
Доказательство:
Пусть прямая М1М2 не перпендикулярна оси OX. Опустим перпендикуляры из точки М1, М, М2 на ось OX и обозначим точки их пересечения с осью OX соответственно через P1, P, P2. На основании теоремы элементарной геометрии о пропорциональности отрезков прямых, заключенных между параллельными прямыми, имеем
P1P \ PP2 = M1M \ MM2= λ
Но P1P= x-x1
PP2= x2-x
Так как числа (x-x1) и (x2-x ) одного и того же знака,
то |x-x1| \ |x2-x| = x-x1 \ x2-x.
Поэтому x-x1 \ x2-x = λ, откуда X= x1+ λx2 \ 1+ λ.
Аналогично получена формула и для Y.
Билет №4. Понятие радиус-вектора. Разложение произвольного вектора по ортам координатных осей на плоскости и в пространстве. Действия с геометрическими векторами в координатной форме. Признак коллинеарности векторов.
