
- •Билет 1
- •1. Понятие о моделировании.
- •2. Моделирование процессов смо
- •Билет 2
- •Модель и расчетная схема. Виды моделирования
- •Виды моделирования.
- •Пример построения алгоритмической модели для одноканальной смо и заявок без приоритета.
- •Билет 3
- •Математическое моделирование. Основные этапы и источники ошибок.
- •Понятие о методах типа Монте-Карло.
- •Билет 4
- •О необходимости тестирования компьютерной модели. Способы тестирования.
- •Терминология для смо. Понятие о простейшем потоке событий.
- •Билет 5
- •5.1. Сравнение некоторых пакетов, расчетов и моделирований.
- •5.2. Марковские процессы.
- •Билет 6
- •6.1. Понятие о системах с сосредоточенными и распределёнными параметрами.
- •6.2. Уравнения Колмогорова.
- •Билет 7
- •7.1. Примеры систем, модель для которых описывается дифференциальными уравнениями.
- •7.2. . Уравнения Колмогорова для замкнутых смо.
- •Билет 8
- •8.1. Сведение произвольной системы оду к системе оду I-го порядка в нормализованном виде Коши. Пример.
- •8.2. Открытые системы массового обслуживания. Уравнения Колмогорова для открытых смо
- •Билет 9
- •9.1 Реализации в среде MathCad математической модели для простейшего осциллятора. Билет 9
- •Билет 10
- •10.1 Пример использования simulink matlab для решения оду 2-го порядка. Билет 11
- •11.1 Методика получения модели механических колебательной системы сосредоточенными параметрами на основе уравнений Лагранжа 2-ого рода
- •11.2 Разложение аппроксиматора по системы базисных функций.
- •12.2 Выполнение среднеквадратичного приближения на основе разложения аппроксиматора по системе базисных функций.
- •13.2. Интегральная квадратичная аппроксимация на отрезке [a, b].
- •Билет 14
- •14.1 Методы решения задачи Коши для оду
- •14.2 Пример MathCad реализующий метод среднеквадратичной аппроксимации
- •Билет 15
- •15.1 Классификация методов решения задачи Коши для оду.
- •15.2 Пример аппроксимации функции 2-ух переменных в MathCad.
- •Билет 16
- •16.1 Метод Эйлера и его модификации для решения оду
- •16.2 Алгебраическое интерполирование.
- •Билет 17
- •Метод типа Рунге-Кутта для решения задачи Коши
- •Интерполирование на основе формулы Лагранжа
- •Билет 18
- •Метод Рунге-Кута 4-ого порядка для решения задачи Коши формулы метода и их реализация в среде MathCad
- •18.2 О наилучшем выборе узлов интерполирования
- •Билет 19
- •Оценка погрешности решения оду. Способ Рунге для оценки такой погрешности.
- •Тригонометрическое интерполирование
- •Билет 20
- •Оценка погрешности решения оду. Способ Рунге для оценки такой погрешности.
- •Использование интерполирования при решении различных задач и реализация в среде MathCad
- •1) Приближенные вычисления функции
- •2) Численное интегрирование
- •3) Численное дифференцирование
- •Билет 21
- •21.1 Методы прогноза и коррекции для решения оду.
- •21.2 Понятие о сплайнах.
- •Билет 22
- •22.1 Понятие о жестких дифференциальных уравнениях.
- •22.2 Эрмитов кубический сплайн.
- •Билет 23
- •23.1 Метод стрельбы для решения граничных задач для оду.
- •23.2 Кубический сплайн дефекта 1. Алгоритм его построения.
- •Билет 24
- •24.1 Задача Бюффона как пример использования методов Монте-Карло при решении детерминированных задач.
- •24.2 Решение системы уравнений, определяющих сплайн, методом прогонки.
- •Билет 25
- •25.2 Обобщенные кубические сплайны.
- •Билет 26
- •26.1 Метод Судзуо-Какутани для решения граничных задач теории потенциалов
- •26.2 Пример использования сплайнов для вычисления площади фигуры
- •Билет 27
- •27.1 Понятие о конкурирующих стратегиях
- •27.2 Параметрический сплайн для приближения кривых.
- •Билет 28
- •28.1 Компонентные уравнения для различных видов подсистем.
- •Механическая поступательная система.
- •Механическая вращательная подсистема
- •Аналоги топологических уравнений
- •Билет 29
- •29.1 Получение эквивалентных схем технических объектов.
- •29.2 Метод получения топологических уравнений математической модели.
- •30.1 Топологические уравнения математической модели на основе матрицы инциденции.
Механическая поступательная система.
Элемент типа R – это элемент вязкого трения.
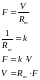
Уравнение массы:

Уравнение упругого
элемента (пружины):

Механическая вращательная подсистема
 - уравнение вязкого
трения
- уравнение вязкого
трения
 – момент инерции
– момент инерции
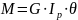 -
уравнение крутильной пружины
-
уравнение крутильной пружины

Как видно, если
ввести соответствия
 ,
то уравнение вязкого затухания в
механической системе окажется по форме
совпадающим с элементом R
в электрической подсистеме. Уравнение
массы эквивалентно уравнению электрической
индуктивности. Уравнение упругого
элемента оказывается таким же как
уравнение конденсатора.Приведем таблицу
соответствия различных типов элементов
для подсистем различной природы.
,
то уравнение вязкого затухания в
механической системе окажется по форме
совпадающим с элементом R
в электрической подсистеме. Уравнение
массы эквивалентно уравнению электрической
индуктивности. Уравнение упругого
элемента оказывается таким же как
уравнение конденсатора.Приведем таблицу
соответствия различных типов элементов
для подсистем различной природы.
Тип подсистемы |
Фазовые переменные |
Компоненты |
|||
Типа I |
Типа U |
Типа R |
Типа С |
Типа L |
|
Электрическая |
Ток |
Падение напряжения |
Сопротивление |
Емкость |
Индуктивность |
Механическая поступательная |
Скорость |
Сила |
Трение (демпфер) |
Упругий элемент (пружина) |
Масса |
Механическая вращательная |
Угловая скорость |
Момент |
Трение |
Крутильная пружина |
Момент инерции |
Гидравлическая |
Давление |
Расход |
Гидравлическое трение |
Гидравлическая емкость |
Гидравлическая индуктивность |
Тепловая |
Tемпература |
Тепловой поток |
Тепловое сопротивление |
Теплоемкость |
----------- |
28.2 Аналоги топологических уравнений для различных видов подсистем.
Аналоги топологических уравнений
Топологические уравнения чаще всего выражают законы равновесия, законы сохранения энергии или условия непрерывности.
Электрическая подсистема.
Уравнения I закона Кирхгофа:
1.
 ,
,
k – номер ветви,
p – множество номеров ветвей, инцидентных данному узлу.
Сумма токов для ветвей, подключенных к данному узлу, равна 0.
2.
 ,
,
j – номер ветви,
q – множество номеров ветвей, инцидентных данному узлу.
Сумма падений напряжений по любому замкнутому контуру равна 0.
Механическая поступательная система.
Аналогом I закона Кирхгофа в данном случае будет:
1.

Сумма абсолютной, переносной и относительной скоростей равна 0.
2.

Сумма всех действующих на систему сил равна 0.
Билет 29
29.1 Получение эквивалентных схем технических объектов.
Будем использовать элемент «масса» при этом один полюс должен быть соединен с так называемым базовым узлом. Применительно такой инерциальной системой является поверхность Земли. Второй полюс элемента представляет собой собственно массу. Через него осуществляется взаимодействие с окружающей средой.
Элемент «трение» включается между контактирующими телами. Если два тела соединены упругой связью, то между ними включается упругий элемент.Внешнее усилие, приложенное к механической системе, отображается элементом «источник силы» F, которая подключается между базовым узлом и тем узлом, к которому подключен полюс «масса», подвергающийся внешнему усилию.
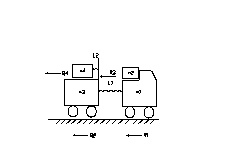
Эквивалентная схема для активного звена автомобиля без учета расположенного на нем груза:

Для автомобиля с массой, расположенной на нем:

Для прицепа с учетом груза:

Окончательная схема выглядит следующим образом:

