Билет 26. Расстояние от точки до плоскости

Пусть плоскость задана уравнением и дана точка .Тогда расстояние от точки до плоскости определяется по формуле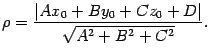

 Доказательство.     Расстояние от точки до плоскости  -- это, по определению, длина перпендикуляра ,опущенного из точки на плоскость

Вектор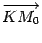 и нормальный вектор n плоскости параллельны, то есть угол между ними равен 0 или ,если вектор n имеет направление противоположное, указанному на рис. 11.9. Поэтому Откуда Координаты точки ,которые нам неизвестны, обозначим . Тогда .Так как ,то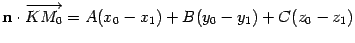 . Раскрыв скобки и перегруппировав слагаемые, получим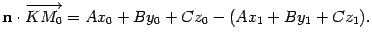 Точка лежит на плоскости ,поэтому ее координаты удовлетворяют уравнению плоскости: . Отсюда находим, что .

27,28,29.Кривые второго порядка на плоскости: эллипс и его свойства

Кривые второго порядка на плоскости: гипербола и ее свойства

Кривые второго порядка на плоскости: парабола и ее свойства

Плоские кривые второго порядка (эллипс, гипербола, парабола). Канонические уравнения кривых второго порядка.

Плоские кривые. Все множество плоских кривых можно разделить на циркульные и лекальные.    Циркульнойназыв. кривую, кот.можно построить с помощью циркуля. Это окружность, овал, завиток.

Эллипс - кривая второго порядка, сумма расстояний от любой точки которой до двух фиксированных точек, называемых фокусами, есть величина постоянная, равная большой оси эллипса.

Парабола - кривая второго порядка, расстояние от любой точки которой до фокуса равно расстоянию от этой точки до некоторой фиксированной прямой, называемой директрисой.

Гипербола - кривая второго порядка, разность расстояний от любой точки которой до двух фокусов есть величина постоянная, равная действительной оси гиперболы. Вдоль действительной оси расположены ветви гиперболы.

Кривая второго порядка — геометрическое место точек, декартовы прямоугольные координаты которых удовлетворяют уравнению вида

в котором по крайней мере один из коэффициентов отличен от нуля.

Каноническое уравнение любой невырожденной кривой второго порядка при помощи подходящего преобразования начала координат может быть приведено к виду

Уравнение выражает тот факт, что невырожденная кривая второго порядка является геометрическим местом точек, отношение расстояний которых от данной точки (фокуса) и от данной прямой (директрисы) постоянно. Кроме того, при кривая является окружностью, при  — эллипсом, при  — параболой, при  — гиперболой.

Уравнение директрисы кривой выражается уравнением а координаты фокуса Директриса перпендикулярна оси симметрии, проходящей через фокус и вершину кривой (фокальная ось). Расстояние между фокусом и директрисой равно