Представление комплексных чисел Алгебраическая форма
Запись
комплексного числа
в
виде
, 
,
называется алгебраической
формой комплексного
числа.
Сумма
и произведение комплексных чисел могут
быть вычислены непосредственным
суммированием и перемножением таких
выражений, как обычно раскрывая скобки
и приводя подобные, чтобы представить
результат тоже в стандартной форме (при
этом надо учесть, что 
):
Тригонометрическая и показательная формы
Если
вещественную
и
мнимую
части
комплексного числа выразить через
модуль 
и
аргумент 
(
, 
),
то всякое комплексное число
,
кроме нуля, можно записать в тригонометрической
форме
Также может быть полезна показательная форма записи комплексных чисел, тесно связанная с тригонометрической через формулу Эйлера:
где 
—
расширение экспоненты для
случая комплексного показателя степени.
Отсюда вытекают следующие широко используемые равенства:
Числовые множества n,z,q,r,c. Пустое множество. Понятие континуума (непрерывности)
Пустое множество — множество, не содержащее ни одного элемента. Из аксиомы объёмности следует, что есть только одно множество, обладающее таким свойством. Пустое множество является своим (тривиальным) подмножеством, но не является своим элементом.
Пустое множество является конечным множеством и имеет наименьшую мощность среди всех множеств. Пустое множество — единственное множество, для которого класс множеств, равномощных ему, состоит из единственного элемента (самого пустого множества). Также, пустое множество — единственное множество, имеющее ровно 1 подмножество (само себя), и единственное множество, равномощное любому своему подмножеству.
Пустое множество тривиальным образом является разрешимым (а значит, перечислимым и арифметическим), транзитивным и вполне упорядоченным множеством (для любого отношения порядка). Пустое множество является наименьшим порядковым числом и наименьшим кардинальным числом. В топологии, пустое множество является одновременно замкнутым и открытым множеством.
-цепочка,
начинающаяся с произвольного множества,
каждый последующий член которой является
элементом предыдущего, всегда через
конечное число шагов завершается пустым
множеством. Таким образом, пустое
множество является «строительным
кирпичиком», из которого строятся все
остальные множества.
В некоторых формулировках теории множеств существование пустого множества постулируется, в других — доказывается.
Свойства пустого множества
Ни одно множество не является элементом пустого множества. Иначе говоря,
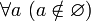и,
в частности,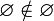 
.Пустое множество является подмножеством любого множества. Иначе говоря,
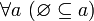и,
в частности,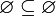 
.Объединение пустого множества с любым множеством равно последнему [указанному множеству]. Иначе говоря,
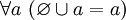и,
в частности,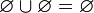 
.Пересечение пустого множества с любым множеством равно пустому множеству. Иначе говоря,
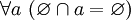и,
в частности,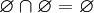 
.Исключение пустого множества из любого множества равно последнему [указанному множеству]. Иначе говоря,
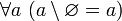и,
в частности, 
.Исключение любого множества из пустого множества равно пустому множеству. Иначе говоря,
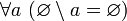и,
в частности,
.Симметрическая разность пустого множества с любым множеством равна последнему [указанному множеству]. Иначе говоря,
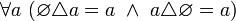и,
в частности,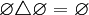 
Декартово произведение пустого множества на любое множество равно пустому множеству. Иначе говоря,
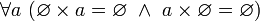и,
в частности,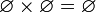 
.Пустое множество — транзитивно. Иначе говоря,
,
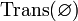где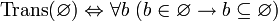 
.Пустое множество — ординал. Иначе говоря,
,
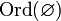где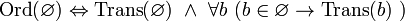 
.Мощность пустого множества равна нулю. Иначе говоря,
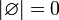.Мера пустого множества равна нулю. Иначе говоря,
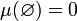
Континуум (от
лат. continuum —
непрерывное) — мощность (или кардинальное
число)
множества всех вещественных
чисел.
Обозначается строчной латинской
буквой c во фрактурном начертании: 
.
Множество, имеющее мощность континуум,
называется континуальным множеством.
Также термин континуум может обозначать само множество вещественных чисел, или даже любое континуальное множество.