3. Наиболее употребительные числовые множества (отрезок, интервал, полуинтервал). Абсолютная величина числа.

Отрезок — множество точек, которое обычно изображается ограниченной частью прямой. Отрезком может называться одно из двух близких понятий в геометрии и математическом анализе. Отрезок прямой — это множество (часть прямой), состоящее из двух различных точек и всех точек, лежащих между ними. При этом сама точка в геометрии является абстрактным объектом, не имеющим никакой длины и вообще каких-либо измеряемых характеристик. Отрезок прямой, соединяющий две точки   и   (которые называются концами отрезка), обозначается следующим образом —  . Если в обозначении отрезка опускаются квадратные скобки, то пишут «отрезок  ». Любая точка, лежащая между концами отрезка, называется его внутренней точкой. Расстояние между концами отрезка называют его длиной и обозначают как  . Интервал (геометрия) — множество точек прямой, заключённых между точками А и В, причём сами точки А и В не причисляются к интервалу, иначе говорят об отрезке Интервал(в математике) – множество действительных чисел, обладающее тем свойством, что вместе с любыми двумя числами содержит любое, лежащее между ними

Полуинтервал — множество точек прямой, заключённых между точками А и В, при этом одна из точек А или В не причисляются к полуинтервалу.

Обозначается   либо   — круглая скобка обозначает что соответствующий конец интервала не принадлежит ему, а квадратная - что принадлежит. Например интервалу   точка   принадлежит, а точка   — не принадлежит.

Абсолютная величина́ или модуль числа   — неотрицательное число, определение которого зависит от типа числа  . Обозначается:  .

В случае вещественного   абсолютная величина есть непрерывная кусочно-линейная функция, определённая следующим образом:

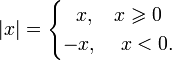
Обобщением этого понятия является модуль комплексного числа  , также иногда называемый абсолютной величиной. Он определяется по формуле:

• Область определения:  .

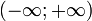• Область значений:  .

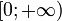• Функция чётная.

• Функция дифференцируема всюду, кроме нуля. В точке 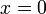  функция претерпевает излом.

Комплексные числа

• Область определения: вся комплексная плоскость.

• Область значений:  .

• Модуль как комплексная функция не дифференцируема ни в одной точке, поскольку условия Коши-Римана не выполнены.

Алгебраические свойства

Для любых   имеют место следующие соотношения:

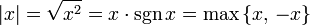•  (см. Функция sgn(x)).

• 

• .

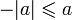Как для вещественных, так и для комплексных   имеют место соотношения:

• , причём 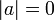  тогда и только тогда, когда  .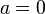

• .

• .

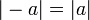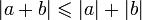•  (неравенство треугольника).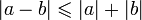

• .

• .

• .

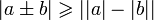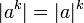• , если 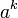  существует.

4. Рациональные и иррациональные числа. Геометрическое представление одномерного пространства. Трансцендентные числа. Мнимая единица.

Рациональное число — число, представляемое обыкновенной дробью  , числитель   — целое число, а знаменатель   — натуральное число, к примеру 1/4. 

Множество рациональных чисел обозначается   и может быть записано в таком виде:

При этом оказывается, что разные записи могут представлять одну и ту же дробь, например,   и  , (все дроби, которые можно получить друг из друга умножением или делением на одно и то же натуральное число, представляют одно и то же рациональное число). Поскольку делением числителя и знаменателя дроби на их наибольший общий делитель можно получить единственное несократимое представление рационального числа, то можно говорить об их множестве как о множестве несократимых дробей со взаимно простыми целым числителем и натуральным знаменателем:

Здесь   — наибольший общий делитель чисел   и  .

Множество рациональных чисел является естественным обобщением множества целых чисел. Легко видеть, что если у рационального числа   знаменатель  , то   является целым числом. Множество рациональных чисел располагается на числовой оси всюду плотно: между любыми двумя различными рациональными числами расположено хотя бы одно рациональное число (а значит, и бесконечное множество рациональных чисел). Тем не менее, оказывается, что множество рациональных чисел имеет счётную мощность (то есть все его элементы можно перенумеровать). Заметим, кстати, что ещё древние греки убедились в существовании чисел, не представимых в виде дроби (например, они доказали, что не существует рационального числа, квадрат которого равен 2).

Иррациональное число — это вещественное число, которое не является рациональным, то есть не может быть представлено в виде дроби  , где   — целые числа,  . Иррациональное число может быть представлено в виде бесконечной непериодической десятичной дроби.

Множество иррациональных чисел обычно обозначается заглавной латинской буквой   в полужирном начертании без заливки. Таким образом:  , т.е. множество иррациональных чисел есть разность множеств вещественных и рациональных чисел.

О существовании иррациональных чисел, точнее отрезков, несоизмеримых с отрезком единичной длины, знали уже древние математики: им была известна, например, несоизмеримость диагонали и стороны квадрата, что равносильно иррациональности числа  .