Первая формулировка

Пусть предложена последовательность точек пространства  :

и пусть эта последовательность ограничена, то есть

где   — некоторое число.

Тогда из данной последовательности можно выделить подпоследовательность

которая сходится к некоторой точке пространства  .

Теорему Больцано — Вейерштрасса в такой формулировке иногда называют принципом компактности ограниченной последовательности.

Расширенный вариант первой формулировки

Нередко теорему Больцано — Вейерштрасса дополняют следующим предложением.

Если последовательность точек пространства   неограничена, то из неё можно выделить подпоследовательность, имеющую предел  .

Для случая   эту формулировку можно уточнить: из любой неограниченной числовой последовательности можно выделить подпоследовательность, имеющую пределом бесконечность определенного знака (  или  ).

Таким образом, всякая числовая последовательность содержит подпоследовательность, имеющую предел в расширенном множестве действительных чисел  .

Вторая формулировка

Следующее предложение является альтернативной формулировкой теоремы Больцано — Вейерштрасса.

Всякое ограниченное бесконечное подмножество   пространства   имеет по крайней мере одну предельную точку в  .

Более подробно, это означает, что существует точка  , всякая окрестность   которой содержит бесконечное число точек множества  .

33. Производная функции. Обозначение производной. Порядок вычисления производной. Примеры вычисления производной. Расположение касательных в случаях f’(x) = 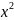и f’(x)=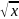

Производная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Процесс вычисления производной называется дифференцированием. Обратный процесс — нахождение первообразной — интегрирование.

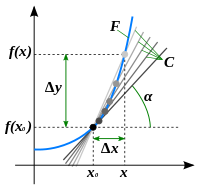Иллюстрация понятия производной

Определение

Пусть в некоторой окрестности точки   определена функция   Производной функции называется такое число  , что функцию в окрестности   можно представить в виде

если   существует.

Определение производной функции через предел

Пусть в некоторой окрестности точки   определена функция   Производной функции   в точке   называется предел, если он существует,

Общепринятые обозначения производной функции   в точке 

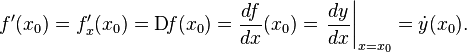
Заметим, что последнее обычно обозначает производную по времени (в теоретической механике).

34. Геометрический смысл производной. Расположение касательных в случаях f’(x) = 0 и f’(x)=

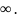
Геометрический и физический смысл производной

Тангенс угла наклона касательной прямой

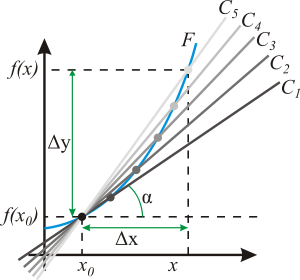
Геометрический смысл производной. На графике функции выбирается абсцисса x₀ и вычисляется соответствующая ордината f(x₀). В окрестности точкиx₀ выбирается произвольная точка x. Через соответствующие точки на графике функции F проводится секущая (первая светло-серая линия C₅). Расстояние Δx = x — x₀ устремляется к нулю, в результате секущая переходит в касательную(постепенно темнеющие линии C₅ — C₁). Тангенс угла α наклона этой касательной — и есть производная в точке x₀.

Если функция   имеет конечную производную в точке   то в окрестности   её можно приблизить линейной функцией

Функция   называется касательной к   в точке   Число  является угловым коэффициентом или тангенсом угла наклонакасательной прямой.

35. Физический смысл производной. Вычисление скорости движения точки.