Элементы векторной алгебры. Векторы. Сложение векторов. Понятие главного вектора. Координаты вектора.
Вектор — понятие, определяемое в разных разделах математики различно.
Понятие вектора в абстрактной алгебре
Пусть 
—
некоторое поле с
аддитивной операцией +, мультипликативной
операцией *, аддитивной
единицей 0
и мультипликативной
единицей 1.
Пусть 
—
некоторая абелева
группа с единицей 
.
Если существует операция
,
такая что для любых 
и
для любых 
выполняются
соотношения:
1. 
,
2. 
,
3. 
,
4. 
,
тогда 
называется векторным
пространством над
полем 
,
элементы V называются векторами,
элементы F —скалярами,
а указанная операция
— умножением
вектора на скаляр.
Понятие вектора в стандартном евклидовом n-мерном пространстве
Вектор
в арифметическом n-мерном пространстве
Является
частным случаем определения вектора в
абстрактной алгебре. Если в качестве 
взять
поледействительных
чисел с
операциями сложения и умножения. 
,
где 
— декартова
степеньмножества
R; для
операцию
«+» зададим следующим образом: 
,
нейтральный элемент:
=(0,…,0),
обратный элемент: 
;
операцию умножения на скаляр: 
.
Тогда вектор, задаваемый кортежем длиной
n, состоящим из действительных чисел
является арифметическим вектором
векторного пространства 
над
полем действительных чисел 
.
n-мерное
пространство задается как
— декартова
степень множества
действительных чисел, точка — как
кортеж 
длины
n из действительных чисел, что соответствует
определению пространства как множества
точек.
Вектор в планарной евклидовой геометрии (связанный вектор) — упорядоченная пара точек, одна из которых называется началом, вторая — концом вектора.
Два вектора равны, если разности по каждой из координат с одинаковыми номерами конечной и начальной точки для этих векторов равны. Эти разности называются пространственными координатами вектора.
Свободный вектор задается классом всех равных связанных векторов и полагается равным каждому из этих связанных векторов и таким образом может быть определен как вектор в арифметическом пространстве (кортеж чисел длины n (пространственных координат равных ему связанных векторов) с операциями сложения и умножения на скаляр).
Результатом операций со связанными векторами принимается вектор, начальная точка которого совпадает с начальной точкой первого слагаемого при сложении векторов и начальной точке исходного вектора при умножении вектора на скаляр.
Нуль-вектор — вектор, начало и конец которого совпадают.
Также существует более распространенное определение вектора как направленного отрезка, но оно требует определения прямой и отрезка в n-мерном пространстве.
Прямая,
на которой лежит ненулевой вектор 
с
началом в точке 
,
заданный свободным вектором с
пространственными координатами
—
множество точек 
,
удовлетворяющее условию:
Отрезок MN —
множество всех точек O(удовлетворяющих
условию 
),
все различные точки которого принадлежат
одной прямой, точки M и N называются
концевыми точками отрезка. Отрезок
называется направленным, если его
концевые точки упорядочены. Если концы
отрезка совпадают, он состоит из 1 точки.
При введение скалярного произведения, угла и длины вектора, задающей расстояние между двумя точками как расстояние между начальной и конечной точками вектора(как показано ниже([1], [2], [3])) векторное пространство становится евклидовым нормированным пространством и при n=3 соответствует модели физического трехмерного пространства; при n=2 — плоскости этого пространства; при n=1 точка соответствует числу на числовой прямой, свободный вектор — разности двух чисел, а длина вектора соответствует модулю; при n=0 существует только одна точка(задается пустым кортежем), декартово произведение содержит только пустой кортеж, соответственно пространство представляет собой точку, есть только нулевой вектор; пространство при n>3 не имеет наглядной геометрической интерпретации, так как физическое пространство трёхмерно.
Скалярное
произведение определяется
по формул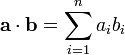е: 
,
[1]
(где 
—
пространственные координаты векторов 
)
Длина
вектора: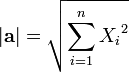 
,
[2]
(где 
—
пространственные координаты вектора.)
Угол
между двумя векторами
(где
—
пространственные координаты векторов
)
определяется через скалярное
произведение:
,
[3]