- •Числа и множества. Числа и цифры. Римская буквенная нумерация. Позиционная система счисления (двоичная, десятичная).
- •Натуральные, простые, отрицательные числа. Основные арифметические действия и законы. Законы ассоциативности (сочетательности), коммутативности и дистрибутивности (распределительности).
- •Наиболее употребительные числовые множества (отрезок, интервал, полуинтервал). Абсолютная величина числа.
- •Комплексные числа
- •Алгебраические свойства
- •Рациональные и иррациональные числа. Геометрическое представление одномерного пространства. Трансцендентные числа. Мнимая единица.
- •Свойства
- •Свойства
- •Степени мнимой единицы
- •Факториал
- •Корни из мнимой единицы
- •Комплексные числа. Комплексно сопряженные числа. Геометрическая, тригонометрическая и показательная форма комплексных чисел.
- •Представление комплексных чисел Алгебраическая форма
- •Тригонометрическая и показательная формы
- •Числовые множества n,z,q,r,c. Пустое множество. Понятие континуума (непрерывности)
- •Свойства пустого множества
- •Свойства
- •Примеры
- •Суть метода математической индукции. Понятие факториала.
- •Формулировка
- •Принцип полной математической индукции
- •Соединения и формула бинома Ньютона.
- •Прогрессии. Арифметическая и геометрическая прогрессии.
- •Примеры
- •Средние величины. Среднее арифметическое, квадратичное, геометрическое. Золотое сечение.
- •Примеры
- •Непрерывная случайная величина
- •Свойства
- •Свойства
- •Математические свойства
- •Понятие функции. Постоянная, возрастающая (убывающая). Четные и нечетные функции.
- •Возрастание и убывание
- •Чётность
- •Периодические функции. Определение периода функции.
- •Примеры
- •Простейшие элементарные функции и их графики (постоянная и степенная).
- •Показательная и логарифмическая функция.
- •Тригонометрические функции.
- •Обратные тригонометрические функции.
- •Функция arcsin
- •Свойства функции arcsin
- •Получение функции arcsin
- •Функция arccos
- •Свойства функции arccos
- •Получение функции arccos
- •Функция arctg
- •Свойства функции arctg
- •Получение функции arctg
- •Функция arcctg
- •Свойства функции arcctg
- •Получение функции arcctg
- •Функция arcsec
- •Функция arccosec
- •Методы построения графиков функций.
- •Аналитическая геометрия плоскости, как двухмерное алгебраическое пространство. Уравнение прямой и окружности.
- •Линии второго порядка (конические сечения).
- •Свойства
- •Группы преобразований
- •Трехмерное евклидово пространство. Поверхности второго порядка.
- •Цилиндрические поверхности
- •Конические поверхности
- •Поверхности вращения
- •Эллиптический параболоид
- •Гиперболический параболоид
- •Центральные поверхности
- •Наиболее употребляемые системы координат.
- •Прямоугольная система координат на плоскости
- •Прямоугольная система координат в пространстве
- •Прямоугольная система координат в многомерном пространстве
- •Прямоугольные координаты вектора
- •Элементы векторной алгебры. Векторы. Сложение векторов. Понятие главного вектора. Координаты вектора.
- •Понятие вектора в абстрактной алгебре
- •Понятие вектора в стандартном евклидовом n-мерном пространстве
- •Вектор в линейном пространстве
- •Сложение
- •Умножение (произведение) векторов. Скалярное, векторное, смешанное и двойное векторное произведение. Скалярное произведение
- •Векторное произведение
- •Смешанное произведение
- •Условие параллельности и перпендикулярности векторов.
- •Неевклидовы геометрии и физическое пространство.
- •Метрика для плоскости
- •Описание метода
- •Вычислительная сложность
- •Предел функции. Теоремы о пределах (предел суммы и разности, произведения частного функций). Приделы некоторых функций ( , , …). Первый и второй замечательные пределы.
- •Первый замечательный предел
- •Второй замечательный предел
- •Бесконечно малые величины. Связь предела функции с бесконечно малыми величинами. Непрерывность функции.
- •Теоремы Больцано и Вейерштрасса с непрерывных функциях на отрезке [a,b].
- •Первая формулировка
- •Расширенный вариант первой формулировки
- •Вторая формулировка
- •Скорость изменения функции
- •Правила дифференцирования общих функций
- •Исследование поведения функций. Возрастаний и убывание функций. Примеры.
- •Исследование поведения функций. Точки локального экстремума функции. Необходимое и достаточное условие локального экстремума.
- •Направление выпуклости и точки перегиба графика функции.
- •Определения и понятия.
- •Интегрирование. Первообразная и неопределенный интеграл.
- •Определенный интеграл. Формула Ньютона – Лейбница.
- •Определение
- •Свойства
Поверхности вращения
Поверхность
называется поверхностью
вращения вокруг
оси
,
если для любой точки ![]() этой
поверхности окружность, проходящая
через эту точку в плоскости
этой
поверхности окружность, проходящая
через эту точку в плоскости ![]() с
центром в
с
центром в ![]() и
радиусом
и
радиусом ![]() ,
целиком принадлежит этой поверхности.
,
целиком принадлежит этой поверхности.
Теорема
(об уравнении поверхности вращения).
Если
в некоторой декартовой
прямоугольной системе
координат поверхность
задана
уравнением ![]() ,
то
—
поверхность вращения вокруг оси
.
,
то
—
поверхность вращения вокруг оси
.
|
Эллипсоид: |
Однополостной гиперболоид: |
Двуполостной гиперболоид: |
Эллиптический параболоид: |
|
|
|
|
|
|
|
|
|
|
В
случае, если ![]() ,
перечисленные выше поверхности являются
поверхностями вращения.
,
перечисленные выше поверхности являются
поверхностями вращения.
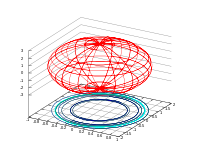
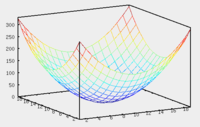
Эллиптический параболоид
Уравнение эллиптического параболоида:
![]()
Если ![]() то
эллиптический параболоид представляет
собой поверхность
вращения,
образованную вращением параболы вокруг
вертикальной оси, проходящей через
вершину и фокус данной параболы.
то
эллиптический параболоид представляет
собой поверхность
вращения,
образованную вращением параболы вокруг
вертикальной оси, проходящей через
вершину и фокус данной параболы.
При сечении эллиптический параболоида плоскостью поверхность порождает эллипс.
При
сечении эллиптический параболоида
плоскостью ![]() или
или ![]() поверхность
порождает параболу.
поверхность
порождает параболу.
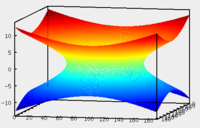
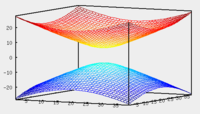
Гиперболический параболоид
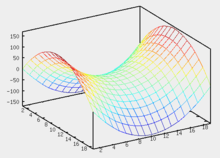 Гиперболический
параболоид.
Гиперболический
параболоид.
Уравнение гиперболического параболоида:
![]()
При сечении гиперболического параболоида плоскостью поверхность порождает гиперболу.
При сечении гиперболического параболоида плоскостью или поверхность порождает параболу.
Ввиду геометрической схожести гиперболический параболоид часто называют «седлом».
Центральные поверхности
Если
центр поверхности второго порядка
существует и единственен, то его
координаты ![]() можно
найти решив систему уравнений:
можно
найти решив систему уравнений:
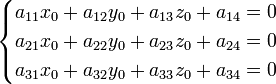
Наиболее употребляемые системы координат.
Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.
В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.
Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).
Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.
Прямоугольная система координат — прямолинейная система координат с взаимно перпендикулярными осями на плоскости или в пространстве. Наиболее простая и поэтому часто используемая система координат. Очень легко и прямо обобщается для пространств любой размерности, что также способствует ее широкому применению.
Декартовой обычно называют прямоугольную систему координат с одинаковыми масштабами по осям, а общей Декартовой системой координат называют аффинную систему координат (не прямоугольную).