Свойства функции arctg

• 

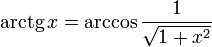• , при x > 0.

Получение функции arctg

Дана функция   На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие   функцией не является. Поэтому рассмотрим отрезок, на котором она строго возрастает и принимает все свои значения только один раз —   На этом отрезке   строго монотонно возрастает и принимает все свои значения только один раз, следовательно, на интервале   существует обратная  , график которой симметричен графику   на отрезке   относительно прямой 

Функция arcctg

График функции y=arcctg x

Арккотангенсом числа m называется такое значение угла x, для которого 

Функция   непрерывна и ограничена на всей своей числовой прямой. Функция  является строго убывающей.

•  при 

•  при 

• 

• 

Свойства функции arcctg

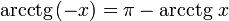•  (график функции центрально-симметричен относительно точки 

•  при любых 

• 

Получение функции arcctg

Дана функция  . На всей своей области определения она является кусочно-монотонной, и, значит, обратное соответствие   функцией не является. Поэтому рассмотрим отрезок, на котором она строго убывает и принимает все свои значения только один раз —  . На этом отрезке   строго убывает и принимает все свои значения только один раз, следовательно, на интервале   существует обратная функция  , график которой симметричен графику   на отрезке   относительно прямой   График симметричен к арктангенсу

Функция arcsec

Функция arccosec

17. Методы построения графиков функций.

18. Аналитическая геометрия плоскости, как двухмерное алгебраическое пространство. Уравнение прямой и окружности.

19. Линии второго порядка (конические сечения).

Конические сечения: окружность,эллипс, парабола (плоскость сечения параллельна образующей конуса),гипербола.

Три основных конических сечения

Коническое сечение или коника есть пересечение плоскости с круговым конусом. Существует три главных типа конических сечений: эллипс, парабола и гипербола, кроме того существуют вырожденные сечения: точка, прямая и пара прямых.Окружность можно рассматривать как частный случай эллипса.

Конические сечения могут быть получены как пересечение плоскости с двусторонним конусом

 (в Декартовой системе координат)

Здесь

 — угол между образующей конуса и его осью.

Если плоскость проходит через начало координат, то получается вырожденное сечение. В невырожденном случае,

• если секущая плоскость пересекает все образующие конуса в точках одной его полости, получаем эллипс,

• если секущая плоскость параллельна одной из касательных плоскостей конуса, получаем параболу,

• если секущая плоскость пересекает обе полости конуса, получаем гиперболу.

Уравнение кругового конуса квадратично, стало быть все конические сечения являютсяквадриками, также все квадрики плоскости являются коническими сечениями (хотя две параллельные прямые образуют вырожденную квадрику которая не может быть получена как сечение конуса, но всё же обычно считается «вырожденным коническим сечением»).

Свойства

• Через любые пять точек на плоскости, никакие три из которых не лежат на одной прямой, можно провести единственное коническое сечение.