1. Числа и множества. Числа и цифры. Римская буквенная нумерация. Позиционная система счисления (двоичная, десятичная).

Число— основное понятие математики, используемое для количественной характеристики, сравнения и нумерации объектов. Цифры — система знаков («буквы») для записи чисел («слов») (числовые знаки). Слово «цифра» без уточнения обычно означает один из следующих десяти («алфавит») знаков: 0 1 2 3 4 5 6 7 8 9 (т. н. «арабские цифры»). Сочетания этих цифр порождают дву-(и более)значные коды и числа. Существуют также много других вариантов («алфавитов»):

• римские цифры (I V X L C D M)

• шестнадцатеричные цифры (0 1 2 3 4 5 6 7 8 9 A B C D E F)

• цифры майя (от 0 до 19)

• в некоторых языках, например, в древнегреческом, в иврите, в церковнославянском, существует система записи чисел буквами и др.

Позиционная система счисления (позиционная нумерация) — система счисления, в которой значение каждого числового знака (цифры) в записи числа зависит от его позиции (разряда).

Двоичная система счисления — позиционная система счисления с основанием 2.

Двоичная система счисления является комбинацией двоичной системы кодирования и показательной весовой функции с основанием равным 2. Положительные целые числа (без знака) записываются в виде:

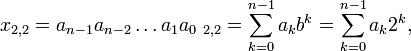
где:

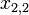•  — представляемое число, первый индекс — основание системы кодирования (размерность множества цифр a={0,1}), второй индекс — основание весовой показательной функции b (в двоично-десятичном кодировании b=10),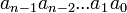

•  — запись числа, строка цифровых знаков,

•  — обозначение основания системы кодирования и основания системы счисления,

•  — количество цифр (знаков) в числе x_2,2,

•  — порядковый номер цифры,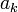

•  — цифры числа x_2,2 из множества a={0,1}, в двоичной системе счисления основание системы кодирования равно 2,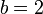

•  — основание показательной весовой функции, основание системы счисления,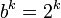

•  — весовая показательная функция, создающая весовые коэффициенты.

Десятичная система счисления — позиционная система счисления по целочисленному основанию 10. Одна из наиболее распространённых систем. В ней используются цифры 1, 2, 3,4, 5, 6, 7, 8, 9, 0, называемые арабскими цифрами. Предполагается, что основание 10 связано с количеством пальцев рук у человека.

Целое число x в десятичной системе счисления представляется в виде конечной линейной комбинации степеней числа 10:

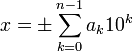, где   — это целые числа, называемые цифрами, удовлетворяющие неравенству 

Обычно для ненулевого числа x требуют, чтобы старшая цифра   в десятичном представлении x была также ненулевой.

Например, число сто три представляется в десятичной системе счисления в виде:

С помощью n позиций в десятичной системе счисления можно записать целые числа от 0 до  , то есть, всего   различных чисел.

Дробные числа записываются в виде строки цифр с разделителем десятичная запятая, называемой десятичной дробью:

где n — число разрядов целой части числа, m — число разрядов дробной части числа.