31) Муфты. Назначение. Классификация. Компенсирующие муфты.

Муфтой называют устройство для соединения концов валов или валов со свободно сидящими на них деталями (зубчатыми колесами, шкивами и т. д.). Основное назначение муфт — передача вращающего момента без изменения его значения и направления.

По управляемости муфты разделяют на:

нерасцепляемые (постоянные), осуществляющие постоянное соединение валов между собой (глухие, жесткие ком-

пенсирующие, упругие компенсирующие);

сцепные управляемые, допускающие во время работы сцепление и расцепление валов с помощью механизма управления (кулачковые, фрикционные); сцепные самоуправляемые, автоматически разъединяющие валы при изменении заданного режима работы машины

(обгонные, центробежные, предохранительные). По степени снижения динамических нагрузок муфты бывают:

жесткие, не сглаживающие при передаче вращающего момента вибрации, толчки и удары; упругие, сглаживающие вибрации, толчки и удары благодаря наличию упругих элементов — пружин, резиновых

втулок и др. Основной характеристикой муфт является передаваемый вращающий момент Т. Муфты подбирают по ГОСТам,

ведомственным нормам, каталогам или проектируют по расчетному моменту.

Жесткие компенсирующие муфты при соединении валов способны компенсировать незначительные радиальные, осевые и угловые смещения, обусловленные неточностями изготовления, монтажа,

особенностями конструкции узлов и деформациями валов при работе. Компенсация отклонений от соосности валов достигается за счет подвижности жестких деталей муфты. Наиболее распространены зубчатые и цепные муфты. Зубчатые муфты компенсируют радиальные, осевые и угловые смещения валов за счет боковых зазоров в зацеплении, обточки зубьев

в тулок по сфере, бочкообразного профиля зуба втулки.

8) Расчет прочности зубьев по напряжениям изгиба

Расчет выполняется при предположениях, что зуб нагружен силой F_H, в зацеплении находится одна пара зубьев, а также силы трения отсутствуют.

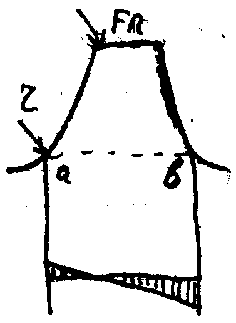
Наибольшее трение в точке b, однако растягивающий эффект в точке a, r – радиус выпуклости зуба,

^{ []}_F

Y_FS – коэффициент, учитывающий форму зуба и концентрацию напряжения

Y_ – коэффициент, учитывающий угол наклона

Y_ – коэффициент, учитывающий перекрытие зубьев. Y_= 1/_£ – для косозубой передачи, Y_ = 1 для прямозубой передачи. _£-коэ. перекр

m выбрать по возможности меньше, z соответственно больше. m=(0,01 ... 0,02)a_W. В случае открытой передачи

7) Расчет зубчатых передач на прочность по контактным напряжениям

Целью расчета является предотвращение усталостного выкрашивания.

z=9600 (8400) прямозубые(косозу)

K_H коэф. Нагрузки.

2 6)Болтовое ненапряжённое соединение нагруженное только осевой силой. ; зависит от свойств материала, режима работы, размера .

27) Болт затянут напряжённое резьбовое соединение (внешние силы не приложены например крышки люков герметичных отсеков). Стержень винта растягивается силой и скручивается силой . 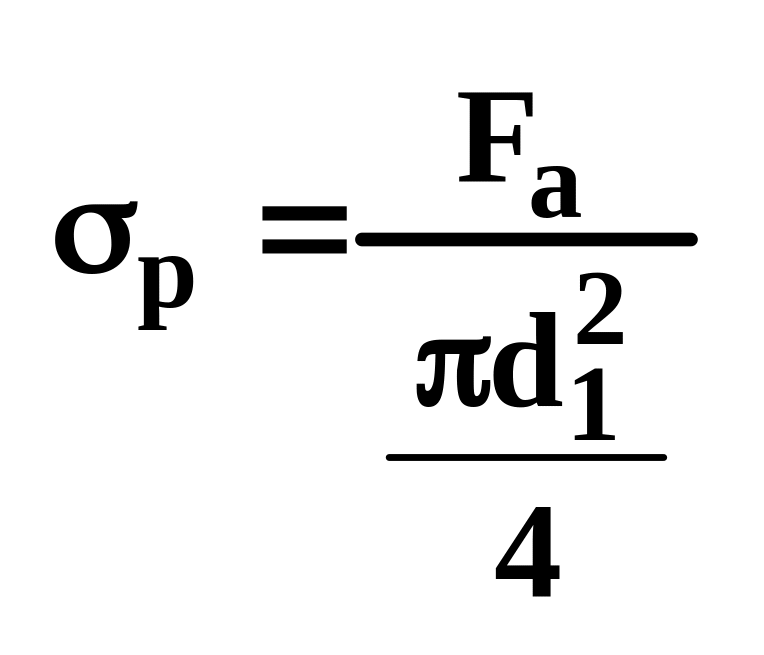; 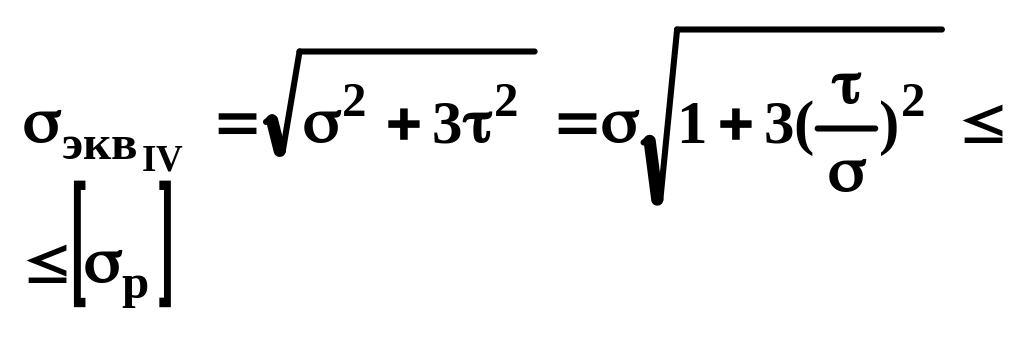по IV теории прочности

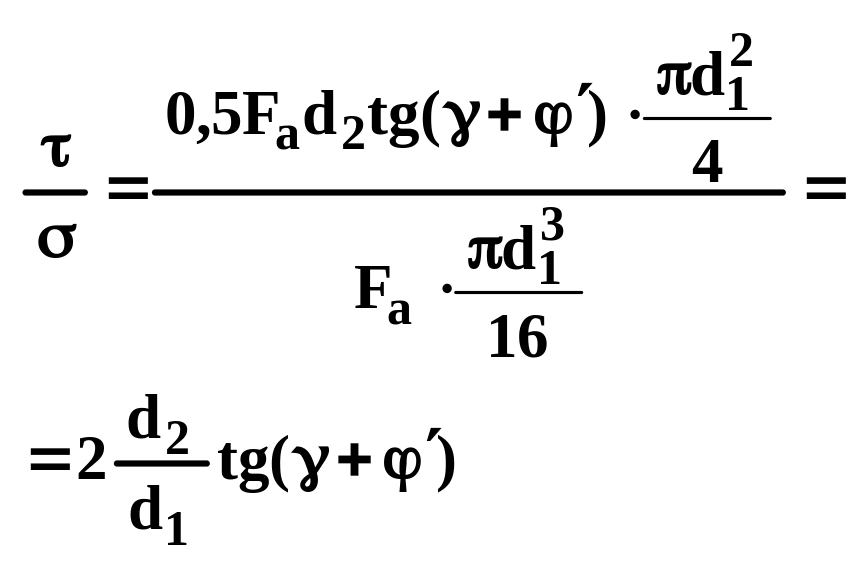
Для метрической резьбы ; ; ; . Для трапециидальной ‑ . Для прямоугольной ‑ . В практических расчётах 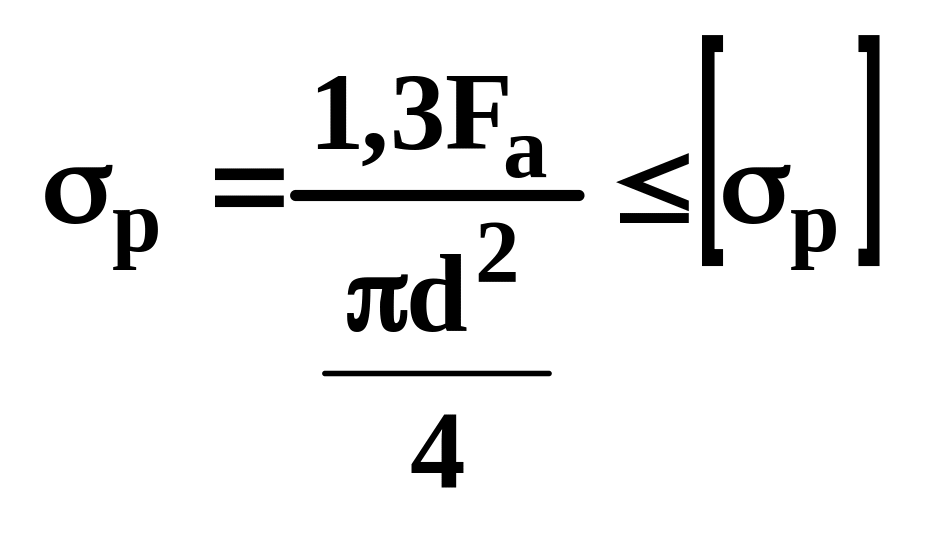с помощью коэффициента учитывают деформацию кручение для затянутого болта.

15) Силы в зубчатой паре

1. В прямозубой передаче действует нормальная сила F_n, которая состоит из следующих сил: (F_n= F_t/ cos )

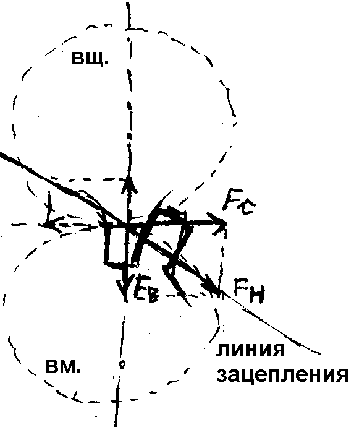
F_t – окружная сила (касательно к начальной окружности), F_R – радиальная сила (к центру окружности). F_t=2000T₁/d_W1, F_R=F_t  tg _W, где _W – угол зацепления.

2) В косозубых (шевронных) передачах действуют следующие силы:

радиальная сила F_R=F_ttg  / cos _W, где _W – угол наклона зуба,

осевая сила (вдоль оси) F_X = F_t  tg _W, окружная сила F_n=F_t / (cos  cos _W).

F_X=0 у шевронных.

15) Силы действующие в конической прямозубой передаче.

Усилия определяются по размерам средних размеров зубьев.

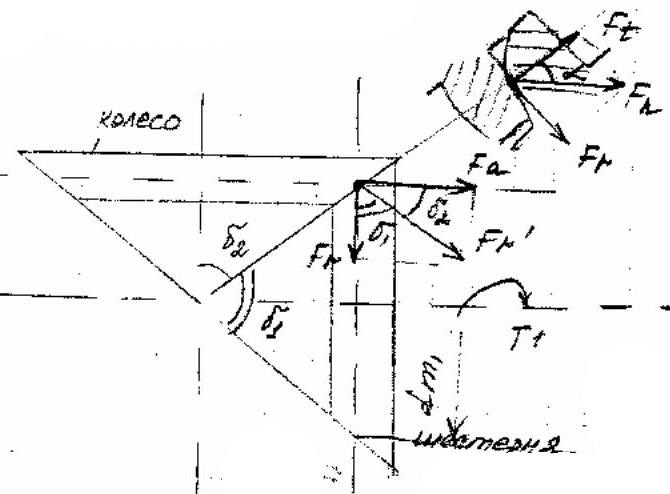
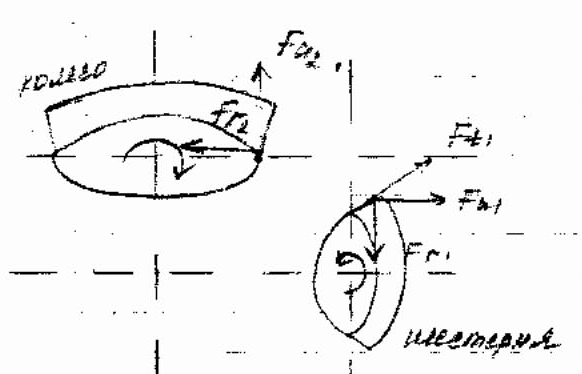
Fа - осевая, F_t – окружная, F_r’– радиальная на среднем диаметре, F_r– радиальная, F_n - нормальная

dm₁ – средний диаметр шестерни, Т – момент.

F_r’=F_ttg ; Fа= F_r’cosδ₂= F_t tg  cosδ₂;

F_r = F_r’cosδ₁= F_t tg  cosδ₁;

F_t – для шестерни против хода вращения, для колеса по ходу

F_r– по радиусу к центру окружности.

Fа= F_r1

Fа₁= F_r2

+(m_n*Z₂/cos)) *0,5= ((Z₁ +Z₂)* m_n)/ /2cos)

Силы червячном в зацеплении

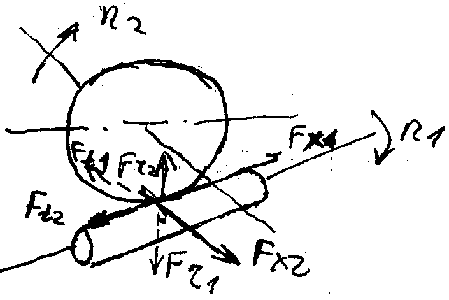
Окружная сила червяка (касательная к начальной окружности)

F_t1 = 2000T₁/d_W1

Осевая червяка (вдоль оси) F_X1= F_t2

Радиальная червяка (к центру окружности) F_R1=F_R2=F_t2tg _£,

_{Окружная колеса Ft2 = 2000T2/dW2}

_{Осевая колеса FX2=Ft1.}

7) Расчет зубчатых передач на сопротивление контактной усталости

Целью расчета является предотвращение усталостного выкрашивания.

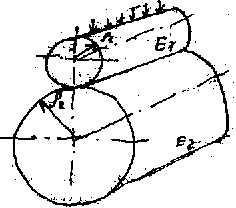
Расчет производится по формуле Герца-Беляева. Зависимость Герца-Беляева для нормальных напряжений в месте контакта двух сухих неподвижных цилиндров из изотропных материалов

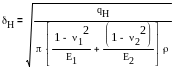q_H – удельная погонная сила по нормали к профилю; ₁, ₂ – коэффициент пуансона; E₁, E₂ – модуль упругости материала,  – радиусы кривизны каждого цилиндра. 1/=1/₁  1/₂, «+» для внешного зацепления, «–» для внутренного зацепления.

Формула Герца-Беляева для пары зубчатых колес

6) Виды разрушений зубьев и виды расчетов

1) Излом зуба (изгиб зуба)

а) мгновенный излом от нарушения статической прочности при значительных нагрузках

б) усталостный излом в результате многократного изгиба зуба.

2) разрушение рабочей поверхности в виде:

а) абразивный износ

б) заедание и волочение из-за отсутствия смазки или недостаточной вязкости

в) выкрашивание – появление и развитие усталостных трещин на поверхности. При этом повышаются контактные напряжения.

г) смятие поверхности.

Наиболее опасным является уставлостный излом и усталостное выкрашивание, другие виды разрушение можно избежать конструктивно.

Выводы: закрытая передача на заданный срок службы должна быть рассчитана на сопротивление контактной усталости _H и проверена на сопротивление по изгибу _F. Для открытых передача на заданный срок службы рассчитывается изгиб и проверяются на сопротивление контактной выносливости.

Расчет передач на сопротивление усталости при изгибе

Расчет выполняется при предположениях, что зуб нагружен силой F_H, в зацеплении находится одна пара зубьев, а также силы трения отсутствуют.

Наибольшее трение в точке b, однако растягивающий эффект в точке a, r – радиус выпуклости зуба,

^{ []}_F

Y_FS – коэффициент, учитывающий форму зуба и концентрацию напряжения

Y_ – коэффициент, учитывающий угол наклона

Y_ – коэффициент, учитывающий перекрытие зубьев. Y_= 1/_£ – для косозубой передачи, Y_ = 1 для прямозубой передачи.

m выбрать по возможности меньше, z соответственно больше. m=(0,01 ... 0,02)a_W. В случае открытой передачи

Расчет по модулю

Если прочность на изгиб является основным критерием работоспособности. Расчет ведется в форме определения модуля по заданным числам зубьев с последующей проверкой контактной прочности (или формула выше)

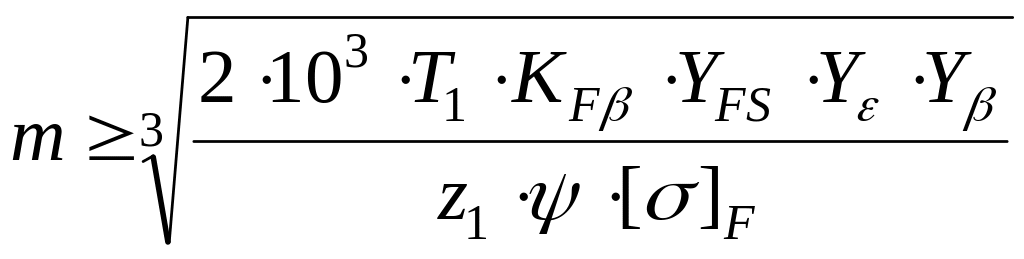
Допускаемые напряжения

Для расчета переменный режим заменяем эквивалентным.

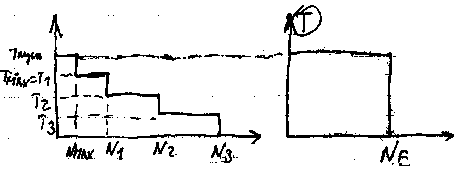
N_E = N_ _H , N_FE=N_ _F, N_ – суммарное число циклов = 60nn_ЗL_h, где

L_h – ресурс работы передачи,

n_З– число зубьев зацеплении,

n– частота вращения.

p = q_H/2, p = q_F. Допускаемые контактные и изгибные напряжения устанавливаются на основе кривых усталости

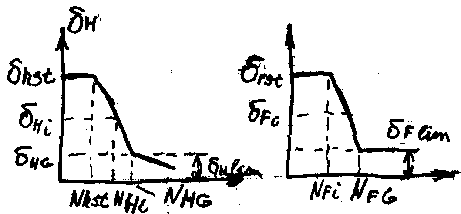
N_HG = 30HB^2,4, N_FG = 410⁶. Если N_HEN_HG, то q_H=6,если N_HE>N_HG, то q_H=20.

11) Особенности геометрии косозубых колес

Зубья косозубых колес располаг. не по образующей делительного цилинд., а составляют с ней угол бетта, оси ост. параллельно

Fа - осевая, F_t – окружная, d -дилительные диаметры, b – ширина колеса,  - наклон зуба, b_п – длина зуба, Pt – окружной шаг, Pn – шаг в нормальном сечении, m_n – нормальный модуль, m_t – окружной модуль, d_a – вершин, d_f - впадин

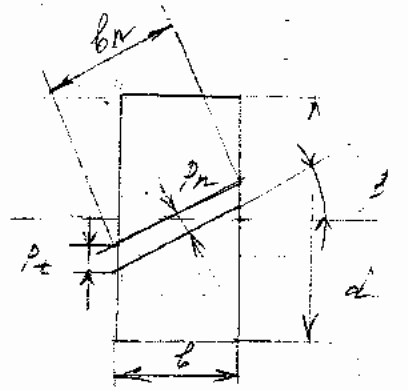
F_а = F_t  tg, Pt= Pn/ cos, m_t= m_n/cos,

h_a= m_n- в головке зуба, h_t= 1.25*m_n- в ножки зуба.

d_a=d+2* h_a= (m_n*Z/cos)+2m_n= =((Z/ cos)+2)*m_n,

*d= Pt*Z d= (Pt*Z)/= =m_t*Z=m_n*Z/cos;

d_f =d-2*1,25* m_n= (m_n*Z/cos)= =2,5* m_t *((Z/ cos)-2,5)*m_n,

d= (d₁+d₂)/2=((m_n*Z₁/cos)+

+(m_n*Z₂/cos)) *0,5= ((Z₁ +Z₂)* m_n)/ /2cos)