4Распределение непрерывных случайных в

. Случайная величина называется непрерывной, если множество ее возможных значений представляет собой не­который конечный или бесконечный промежуток числовой оси.

Под основными числовыми характеристиками непрерывной слу­чайной величины понимают, как и в случае дискретной случай­ной величины, математическое ожидание, дисперсию и среднее квадратическое отклонение.

Как и для дискретной величины, математическое ожидание представляет собой среднее значение этой величины, а дисперсия и среднее квадратическое отклонение являются усредненными характеристиками степени разброса возможных значений этой величины относительно ее математического ожидания.

Однако формулы, определяющие математическое ожидание М(Х) =μ и дисперсию D(Х)= σ ² непрерывной случайной величи­ны, отличаются от соответствующих формул для дискретной ве­личины и в общем случае имеют соответственно вид M(X)= μ= ∫x f(x)dx

D(X)= σ ² =∫(x- μ )² f(x)dx

Среднее квадратическое отклонение, как и для дискретной случайной величины, определяется формулой:

σ= √D(X) (8.27)

5) Непрерывные и дискретные случайные Бернуллим

Случайной величиной, величина принимающая значение в зависимости от стечения случайных обстоятельств. Случайная величина дискретной,а если она принимает счетное множество значений .Непрерывная случайная величина принимает любые значения внутри некоторого интервала: Биномиальный закон (распределение Бернулли)В общей форме биномиальный закон описывает осуществление признака в n испытаниях с возвратом. Наглядной схемой таких испытаний является последовательный выбор с возвращением шаров из урны, содержащей m₁ белых и m₂ чёрных шаров. Если X — число появления белых шаров в выборке из   шаров, то p=m₁\(m₁₊m₂) ; q=1-p

где p,q — вероятность появления при одном извлечении соответственно белого и чёрного,

Производящая функция биномиального распределения задаётся формулой

Основные характеристики биномиального распределения (математическое ожидание и дисперсия):M(X)=np; D[x]=npq

пример Пример 1. Вероятность получения бракованного изделия равна 0,01. Какова вероятность того, что среди 100 изделий окажется не более 3 бракованных?

Решение. Пусть  . Согласно биномиальному закону и закону сложения имеем

6) Закон распределения Пуассона

Непрерывные величины принимают бесконечное число возможных значений в конечном, или в бесконечном интервалах изменения..Дискретные величины могут принимать конечное, счетное число случайных значений..Распределению Пуассона удовлетворяют вероятности появления заданного кол-ва редко происходящих случайных событий, наблюдаемый в серии из большого числа независимых опытов. Это распределение описывает дискретные, целочисленные неотрицательные случайные величины, появляющиеся с вероятностью р, много меньшей 1.

P_n(m)= /m!)* ,

Где m-число ожидаемых событий, P_n(m)-вероятность появления m искомых событий в серии из n независимых испытаний, μ-параметр распределения, совпадающий с математическим ожиданием, е-основание натурального логарифма.

Формулы для вычисления математического ожидания случайной величины.

Для дискретных величин M=∑Xi * Pi

Для непрерывных величин M=

Формулы для вычисления дисперсии случайной величины, среднеквадратического отклонения

Для дискретных величин D=∑(Xi-Xср)² * Рi

Для непрерывных величин D= ² * f(x)dx

Среднеквадратическое отклонение δ=

7) Плотность вероятности. Нормальн

Случайная величина (далее СВ) – величина, которая принимает значение в зависимости от стечения случайных обстоятельств. СВ называется дискретной (далее – ДСВ), если она принимает счетное множество значений. СВ называется непрерывной (далее – НСВ), если она принимает любые значения внутри некоторого интервала. Вероятность- предел, к которому стремится частота события при неограниченном увеличении числа испытаний. (статистическое определение)

P(A)=lim_n→∞(m/n)

- отношение благоприятствующих случаев к общему числу равновозможных случаев к общему числу равновозможных несовместимых событий. (классическое опредедение) P(A)=(m/n)

Распределение вероятностей — закон, описывающий область значений СВ и вероятности их принятия.

1)Распределение ДСВ. Дискретная величина (Х) считается заданной, если указаны ее возможные значения (x_n) соответствующие им вероятности Р(х_n)=p_n. Совокупность Х и Р называется распределением ДСВ.

2.Распределение НСВ. dP=f(x)dx; dP – вероятность того, что НСВ Х принимает значения между х и х+dх. Вероятность dP прямо пропорциональна интервалу dx.

f(x) – плотность вероятности (функция распределения вероятностей). Показывает, как изменяется вероятность, отнесенная к интервалу dx случайной величины, в зависимости от самой этой величины. f(x)=dP/dx ; F(x)= - функция распределения НСВ. Равна вероятности того, что СВ

принимает значения, меньшие х.;F(x)=(-∞<X<x)Нормальный закон распределения (закон Гаусса). СВ распределена по этому закону, если плотность вероятности имеет вид

M(X) – мат.ожидание СВ, σ – среднее квадратическое отклонение, σ²- дисперсия СВ.

Дисперсия СВ – МО отклонения случайной величины от ее МО.

D(X)=M[X-M(X)]

Удобная формула: D(X)=M(X²)-[M(X)]²

Кривая закона носит колокообразную форму, симметричную относительно прямой х=а (центр рассеивания). В точке х=а функция достигает максимума.

8) Стандартное нормальное распределение

Для непрерывных случ.величин описывается законом Гаусса. Распределение вероятностей, которое задается функцией плотности распределения:

где μ —математическое ожидание

σ² — дисперсия.

σ – среднее квадратич. отклонение этой величины

График симметричен относительно вертик.прямой Хmax = μ.(снизу сигма)

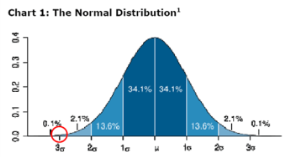
Стандартный интервал а</=х</=b

Вероятность попадания в него случайной величины

Р(а</=х</=b)= а

Доверительная вероятность α – некоторая заданная вероятность, с которой случ.величина попадает в определённый интервал.

Такой интервал – доверительный

Стандартные интервалы

(вместо < должно быть </=)

М- σ <х< М+ σ (α = 68%)

М- 2σ <х< М+ 2σ (α = 95%)

М- 3σ <х< М+ 3σ (α = 99,7%)