Числовые ряды.

Упорядоченный ряд чисел - числовая последовательность.

а1, а2, а3...аn – общий член последовательности

аn=f(n) – ф-я натурального аргумента

Числовой ряд а1+а2,+а3...+an+...=сигма an

Числовой ряд  называется сходящимся, если существует конечный предел последовательности частичных сумм  . Если предел последовательности частичных сумм числового ряда не существует или бесконечен, то ряд  называется расходящимся.

Виды рядов

-Знакоположительные ряды (ЗПР)

an>0

-Знакопеременные ряды

Частный случай –Знакочередующиеся ряды, -Степенные ряды.

Сумма n первых членов

q не равно 1

|q|>1 – Сумма  беск., |q|<1 qⁿ 0 Sn  b1/(1-q)

Обобщенный гармонический ряд.

Сумма вида  , где s – некоторое действительное число, называется обобщенно гармоническим числовым рядом.Частичные суммы членов ряда

S1=a1, S2=a1+a2, S3=a1+a2+a3, Sn=a1+a2+…an – энная частичная сумма

остаток ряда (Ряд, полученный отбрасыванием от исходного n первых членов)

Если существует предел частичных сумм, т.е. limSn=S (S const), то числовой ряд сходится, значение предела S наз-ют суммой ряда. Если же предел частичных сумм равен бесконечности или не существует, то ряд расходится

Обобщенно-гармонический

Сигма 1/n^s если S>1ряд сходится, S<1ряд расходится

Геометрический ряд.

Геометрический ряд

|q|>=1  ряд расходится, |q|<1 ряд сходится

сумма первых n членов геометрической прогрессии

Необходимый признак сходимости ЧР.

Если ряд (сигма) сходится, то lim an=0, но обратное утверждение не может быть верным.

Если lim an=0, то ряд (сигма) либо сходится, либо расходится.

-гармонический ряд, расходится хотя lim 1/n=0

Пример. Докажите сходимость числового ряда  . Решение. Запишем ряд в другом виде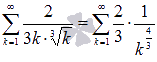 

Числовой ряд   сходится, так как обобщенно гармонический ряд   является сходящимся

при s > 1, а в силу второго свойства сходящихся числовых рядов будет сходится и ряд с числовым коэффициентом 

Признаки сравнения ЗПР

Пусть сигма Un –исследуемый ряд, сигма Vn эталонный ряд

1. Если эталонный ряд сходится и Un<,=Vn, то исходный ряд сходится.

2. Если эталонный ряд расходится и Un>,=Vn, то исходный ряд расходится

3. Если предел отношения Nого члена исходного ряда к Nому члену эталонного ряда существует, конечен и не равен нулю, т.е. lim Un/Vn=k (k-const), k не равно 0, то исходный ряд ведет себя так же, как и эталонный.

Признак сравнения в предельной форме целесообр исследовать, если Un равно отношению многочленов и/или корней из многочленов.

1.

2. Эталонный ряд сигма 1/n-расходится, применим предельный признак

 исходный ряд ведет себя так же, как и эталонный, расходится.

.

Признак Даламбера.

Пусть lim (Un+1)/Un=эль маленькая.

Если l>1, то ряд расходится

Если 0<,=l<1, то ряд сходится

Если l=1, то требуется подобрать другой метод исследования

Признак Даламбера целесообр использовать, если Un содержит показательную ф-ю an и/или n! Факториал всегда побеждает степень

Применяем признак Даламбера

,

0<1  ряд сходится.

Интегральный признак Коши.

Интегральный признак Коши

Пусть задан ЗПР, для Nого члена которого выполняются условия, члены ряда монотонно убывают

Сигма Un-ЗПР

Un=f(x) ф-я f(x) x пренадл [1;+беск]

f(x)>0, ф-ия непрерывна, убывает

Если инт сходится - ряд сходится, если инт расходится – ряд расходится

, ,

Интеграл сходится, ряд сходится.

Знакопеременный ряд. Теорема об абсолютной сходимости.

Абсолютная величина – величина по модулю.

Пусть дан знакопеременный ряд. Если ряд сходится из абсол величин, то данный знакопеременный ряд сходится абсолютно.

П ример. Докажите, что знакопеременный числовой ряд   абсолютно сходится. Решение. Соответствующих знакоположительный ряд будет иметь вид  . Для него выполняется необходимое условие сходимости ряда, так как  . Возьмем сходящийся знакоположительный ряд  и воспользуемся вторым признаком сравнения: .

Следовательно, ряд  сходящийся, поэтому, исходный ряд сходится абсолютно.