Бесконечно малая величина

Последовательность   называется бесконечно малой, если  . Например, последовательность чисел   — бесконечно малая.

Функция называется бесконечно малой в окрестности точки  , если  .

Функция называется бесконечно малой на бесконечности, если   либо  .

Также бесконечно малой является функция, представляющая собой разность функции и её предела, то есть если  , то  ,  .

[Править]Бесконечно большая величина

Во всех приведённых ниже формулах бесконечность справа от равенства подразумевается определённого знака (либо «плюс», либо «минус»). То есть, например, функция  , неограниченная с обеих сторон, не является бесконечно большой при  .

Последовательность   называется бесконечно большой, если  .

Функция называется бесконечно большой в окрестности точки  , если  .

Функция называется бесконечно большой на бесконечности, если   либо  .

[Править]Свойства бесконечно малых

• Сумма конечного числа бесконечно малых — бесконечно малая.

• Произведение бесконечно малых — бесконечно малая.

• Произведение бесконечно малой последовательности на ограниченную — бесконечно малая. Как следствие, произведение бесконечно малой на константу — бесконечно малая.

• Если   — бесконечно малая последовательность, сохраняющая знак, то 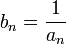  — бесконечно большая последовательность.

12) Рассмотрим теоремы о правилах предельного перехода. Т.1: Предел постоянной равен самой постоянной Доказательство следует из определения предела функции, так как если с = const.

Т.2: (о связи функции с ее пределом). Для того чтобы   необходимо и достаточно выполнение равенства где — б.м. при х а

— б.м., х а)

Запишем цепочку равносильных утверждений, следующих из определения предела функции и определения б.м.:

Т.3: Предел суммы конечного числа функций, имеющих пределы при х а, равен сумме их пределов

Пусть тогда по теореме 2 име-

ем где — б.м. при

х а, следовательно,  Используя лемму 1 о б.м., заключаем, что — б.м. при

 и по теореме 2 получаем равенство  b1 + b2

Т.4: Предел произведения конечного числа функций, имеющих пределы при х а, равен произведению пределов Методика доказательства аналогична доказательству Т.3. Следствие. Постоянный множитель можно выносить за знак предела.

Т.5: Предел отношения двух функций, имеющих пределы при х а, равен отношению их пределов (если предел знаменателя не нуль), т.е.

Пусть тогда, используя Т.2, аналогично доказательству Т.3 запишем

где  Числитель последней дроби по леммам о б.м. является б.м. Покажем, что является функцией ограниченной, тогда дробь по лемме 2 о б.м. является б.м., и по Т.2:

Имеем в некоторой окрестности т. а для любого > 0 вследствие справедливости

т.е. ограниченность доказана

13) Произво́дная (функции в точке) — основное понятие дифференциального исчисления, характеризующее скорость изменения функции (в данной точке). Определяется как предел отношения приращения функции к приращению ее аргумента при стремлении приращения аргумента к нулю, если такой предел существует. Функцию, имеющую конечную производную (в некоторой точке), называют дифференцируемой (в данной точке).

Процесс вычисления производной называется дифференци́рованием. Обратный процесс — нахождение первообразной — интегрирование.

Пусть в некоторой окрестности точки   определена функция   Производной функции называется такое число  , что функцию в окрестности  можно представить в виде

если   существует.