1)Система координат — комплекс определений, реализующий метод координат, то есть способ определять положение точки или тела с помощью чисел или других символов. Совокупность чисел, определяющих положение конкретной точки, называется координатами этой точки.

В математике координаты — совокупность чисел, сопоставленных точкам многообразия в некоторой карте определённого атласа.

В элементарной геометрии координаты — величины, определяющие положение точки на плоскости и в пространстве. На плоскости положение точки чаще всего определяется расстояниями от двух прямых (координатных осей), пересекающихся в одной точке (начале координат) под прямым углом; одна из координат называется ординатой, а другая — абсциссой. В пространстве по системе Декарта положение точки определяется расстояниями от трёх плоскостей координат, пересекающихся в одной точке под прямыми углами друг к другу, или сферическими координатами, где начало координат находится в центре сферы.

В географии координаты — широта, долгота и высота над известным общим уровнем (например, океана). См. географические координаты.

В астрономии координаты — величины, при помощи которых определяется положение звезды, например, прямое восхождение и склонение.

Небесные координаты — числа, с помощью которых определяют положение светил и вспомогательных точек на небесной сфере. В астрономии употребляют различные системы небесных координат. Каждая из них по существу представляет собой систему полярных координат на сфере с соответствующим образом выбранным полюсом. Систему небесных координат задают большим кругом небесной сферы (или его полюсом, отстоящим на 90° от любой точки этого круга) с указанием на нём начальной точки отсчёта одной из координат. В зависимости от выбора этого круга системы небесных координат называлась горизонтальной, экваториальной, эклиптической и галактической.

Наиболее используемая система координат — прямоугольная система координат (также известная как декартова система координат).

Координаты на плоскости и в пространстве можно вводить бесконечным числом разных способов. Решая ту или иную математическую или физическую задачу методом координат, можно использовать различные координатные системы, выбирая ту из них, в которой задача решается проще или удобнее в данном конкретном случае. Известным обобщением системы координат являются системы отсчёта и системы референции.

ДЕКА́РТОВА СИСТЕ́МА КООРДИНА́Т, прямолинейная система координат на плоскости или в пространстве (обычно с взаимно перпендикулярными осями и одинаковыми масштабами по осям). Названа по имени Р. Декарта.

Декарт впервые ввел координатную систему, которая существенно отличалась от общепринятой в наши дни. Он использовал косоугольную систему координат на плоскости, рассматривая кривую относительно некоторой прямой с фиксированной системой отсчета. Положение точек кривой задавалось с помощью системы параллельных отрезков, наклонных или перпендикулярных к исходной прямой. Декарт не вводил второй координатной оси, не фиксировал направления отсчета от начала координат. Только в 18 в. сформировалось современное понимание координатной системы, получившее имя Декарта

Полярная система координат — двумерная система координат, в которой каждая точка на плоскости определяется двумя числами — полярным углом и полярным радиусом.

Полярная система координат задаётся лучом, который называют нулевым или полярной осью. Точка, из которой выходит этот луч, называется началом координат или полюсом. Любая точка на плоскости определяется двумя полярными координатами: радиальной и угловой. Радиальная координата (обычно обозначается ) соответствует расстоянию от точки до начала координат. Угловая координата, также называется полярным углом или азимутом и обозначается , равна углу, на который нужно повернуть против часовой стрелки полярную ось для того, чтобы попасть в эту точку.^[1]

Определённая таким образом радиальная координата может принимать значения от нуля до бесконечности, а угловая координата изменяется в пределах от 0° до 360°. Однако, для удобства область значений полярной координаты можно расширить за пределы полного угла, а также разрешить ей принимать отрицательные значения, что отвечает повороту полярной оси по часовой стрелке.

Связь между декартовыми и полярными координатами

Пару полярных координат и можно перевести в Декартовы координаты и путём применения тригонометрических функций синуса и косинуса:

в то время как две декартовы координаты и могут быть переведены в полярную координату :

(по теореме Пифагора).

Для определения угловой координаты следует принять во внимание два следующие соображения:

• Для 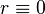, может быть произвольным действительным числом.

• Для 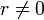, чтобы получить уникальное значение , следует ограничиться интервалом в 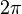. Обычно выбирают интервал 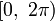или .

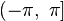Для вычисления в интервале , можно воспользоваться такими уравнениями ( обозначает обратную функцию к тангенсу):

Для вычисления в интервале , можно воспользоваться такими уравнениями:^[14]

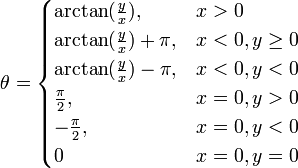
Учитывая, что для вычисления полярного угла не достаточно знать отношение к , а ещё нужны знаки одного из этих чисел, многие из современных языков программирования имеют среди своих функций помимо функции atan, определяющей арктангенс числа, ещё и дополнительную функцию atan2, которая имеет отдельные аргументы для числителя и знаменателя. В языках программирования, поддерживающих необязательные аргументы (например, в Common Lisp), функция atan может получать значение координаты .

2) Уравнение прямой на плоскости - определение.

Пусть на плоскости зафиксирована прямоугольная декартова система координат Oxy и в ней задана прямая линия.

Прямая, как и любая другая геометрическая фигура, состоит из точек. В фиксированной прямоугольной системе координат каждая точка прямой имеет свои координаты – абсциссу и ординату. Так вот зависимость между абсциссой и ординатой каждой точки прямой в фиксированной системе координат, может быть задана уравнением, которое называют уравнением прямой на плоскости.

Другими словами, уравнение прямой на плоскости в прямоугольной системе координат Oxy есть некоторое уравнение с двумя переменными x и y, которое обращается в тождество при подстановке в него координат любой точки этой прямой.

Осталось разобраться с вопросом, какой вид имеет уравнение прямой на плоскости. Ответ на него содержится в следующем пункте статьи. Забегая вперед, отметим, что существуют различные формы записи уравнения прямой, что объясняется спецификой решаемых задач и способом задания прямой линии на плоскости. Итак, приступим к обзору основных видов уравнения прямой линии на плоскости.

Всякое уравнение первой степени с двумя переменными x и y вида , где А, В и С – некоторые действительные числа, причем А и В одновременно не равны нулю, задает прямую линию в прямоугольной системе координат Oxy на плоскости, и всякая прямая на плоскости задается уравнением вида .

 Общее уравнение прямой Уравнение Ax+By+C=0 ( где A, B и C могут принимать любые значения, лишь бы коэффициенты A, B не были равны нулю оба сразу) представляет прямую линию. Всякую прямую можно представить уравнением этого вида. Поэтому его называют общим уравнением прямой .

 3. Ах+Ву+С=0 1) Если A =0, то уравнение представляет прямую, параллельную оси Ох (у = ). Пример 1. Графиком уравнения у=-10 является прямая, параллельная оси Ох и проходящая через точку (0;-10). О -10 х у

 4. Ах+Ву+С=0 2) Если В=0, то уравнение представляет прямую, параллельную оси Оу (х= ). Пример 2 . Графиком уравнения х=6 является прямая, параллельная оси Оу и проходящая через точку (6;0). О 6 у х

 5. Ах+Ву+С=0 3) Когда В=0, то у= Уравнение у=кх+ m , где к= , а m = называется уравнением прямой с угловым коэффициентом к. 4) Если С=0, то есть уравнение Ах+Ву+С=0 не содержит свободного члена, то оно представляет прямую, проходящую через начало координат.

 6. Ах+Ву+С=0 (у= , то есть у=кх – где к – угловой коэффициент прямой. Ясно, что к= , где Х 0 и У 0 координаты произвольной точки прямой, Х 0 =0). х у у 0 х 0 1 0 1

 7. Пример 3. Составить уравнение прямой, изображенной на рисунке. Решение. Так как прямая проходит через начало координат, то она задается уравнением у=кх. Определим угловой коэффициент этой прямой. Возьмем к примеру точку А этой прямой, тогда к= , то есть к= . Значит, к=-2 и уравнение данной прямой имеет вид: у=-2х. 0 у х -1 1 1 -1 А 2

 8. Пример 4. Составить уравнение прямой , изображенной на рисунке. Решение. Данная прямая получена из прямой у=кх смещением последней на 3 ед. отрезка вверх вдоль оси Оу. Прямые у=кх и данная параллельны, следовательно, их угловые коэффициенты равны. Определив угловой коэффициент прямой у=кх (к= ), получим, что угловой коэффициент данной прямой равен -2. А так как данная прямая пересекает ось Оу в точке с ординатой 3, то в уравнении данной прямой (у=кх+ m ), к=-2, m= 3. Искомое уравнение имеет вид у= =-2х+3. у=кх у х А

 9. Теоремы Уравнение изображенной прямой можно получить и иначе, если иметь ввиду следующие утверждения. Теорема 1. Если прямая отсекает на осях отрезки а и в (не равные нулю), то ее можно представить уравнением =1.

 10. Теорема 2. Уравнение =1 представляет прямую, отсекающую на осях (считая от начала координат) отрезки а и в. Уравнение =1 называется уравнением прямой в отрезках (ясно, что а=0, в=0).

 11. Вывод уравнения прямой в отрезках. Уравнение прямой в отрезках легко получается либо из общего уравнения прямой, либо из уравнения прямой с угловым коэффициентом. Пусть у=кх+ m – уравнение прямой с угловым коэффициентом. Приведем его к виду =1.

 12. у=кх+ m Для этого перенесем слагаемое кх в левую часть уравнения, изменив его знак на противоположный и разделим обе части полученного равенства на m . Получим следующее уравнение =1. Перепишем это уравнение в виде =1. Учтем, что = . Следовательно, = . Обозначив буквой «а», а m – буквой «в» получим искомое уравнение прямой в отрезках =1.

 13. Рассмотрим следующий пример Пример 5. Составить уравнение прямой, изображенной на рисунке. Решение. Прямая отсекает отрезки -2 на оси Оу и 3 – на оси Ох. Поэтому ее уравнение можно записать так:1) =1 или =1. Из последнего уравнения можно получить уравнение прямой в общем виде и уравнение прямой с угловым коэффициентом. у -1 х 1 1 -1 0 3 -2

 14. Пример 5. 2) =1 6. 2х-3у=6. 2х-3у-6=0. 3) =1. = 1 2. у= -2. В ответе можно записать любое из уравнений 1), 2) или 3). Кроме того, уравнение прямой в отрезках удобно использовать для построения этой прямой на чертеже.

 15. Уравнение прямой, проходящей через две точки. Теперь, допустим, нужно записать уравнение прямой проходящей через две точки А (1;-2) и В (-1;4). Очевидно, что для решения этой задачи надо составить и решить систему уравнений относительно к и m , где х 1 =1, у 1 =-2, х 2 =-1, у 2 =4. И, найдя значения к и m , подставить их в уравнение у=кх+ m . Всякий раз решать подобные задачи таким способом довольно-таки нерационально. у 2 =кх 2 + m . у 1 =кх 1 + m ,

 16. Решим эту задачу в общем виде. Пусть требуется составить уравнение прямой, проходящей через две различные точки (х 1 ;у 1 ) и (х 2 ;у 2 ) такие, что х 1 =х 2 , у 1 =у 2 . Так как прямая проходит через эти точки, то их координаты удовлетворяют уравнению прямой у=кх+ m .

 17. Решим эту задачу в общем виде. Решим систему уравнений относительно к и m . Найдя значения к и m , подставим их в уравнение у=кх+ m . Итак, Уравнение прямой примет вид: у= х+у 1 - х 1. у 2 =кх 2 + m . у 1 =кх 1 + m , m =у 1 -кх 1 , у 2 =кх 2 +у 1 -кх 1 . m =у 1 -кх 1 , у 2 =кх 2 + m . у 1 =кх 1 + m , к= . (у 2 -у 1 )=к (х 2 -х 1 ). m =у 1 -кх 1 , m =у 1 - х 1 , к= .

 18. Преобразуем его у-у 1 = х- х 1, у-у 1 = (х-х 1 ). (у-у 1 ) (х 2 -х 1 )=(у 2 -у 1 ) (х-х 1 ) (х 2 -х 1 ) (у 2 -у 1 ), Мы получили уравнение прямой, проходящей через две различные точки (х 1 ;у 1 ) и (х 2 ;у 2 ), причем х 1 =х 2, у 1 =у 2 . , ,

 19. (у-у 1 ) (х 2 -х 1 )=(у 2 -у 1 ) (х-х 1 ) А что если х 2 =х 1 (при условии, что у 2 =у 1 ) или у 2 =у 1 (при условии, что х 2 =х 1 )? В этом случае уравнение ( ) будет выглядеть так: (у 2 - у 1 ) (х-х 1 )=0 или (у-у 1 ) (х 2 -х 1 )=0. Откуда получим уравнения: х=х 1 или у=у 1 . То есть уравнения прямых, параллельных координатным осям .

3) Если уравнения прямой заданы в общем виде

A₁x + B₁y + C₁ = 0,         

A₂x + B₂y + C₂ = 0,     (6)

угол между ними определяется по формуле

     (7)

Условия параллельности двух прямых:

а) Если прямые заданы уравнениями (4) с угловым коэффициентом, то необходимое и достаточное условие их параллельности состоит в равенстве их угловых коэффициентов:

k₁ = k₂.     (8)

Для случая, когда прямые заданы уравнениями в общем виде (6), необходимое и достаточное условие их параллельности состоит в том, что коэффициенты при соответствующих текущих координатах в их уравнениях пропорциональны, т. е.

     (9)

Условия перпендикулярности двух прямых:

а) В случае, когда прямые заданы уравнениями (4) с угловым коэффициентом, необходимое и достаточное условие их перпендикулярности заключается в том, что их угловые коэффициенты обратны по величине и противоположны по знаку, т. е.

    

4)  Вектор – одно из основных геометрических понятий. Вектор характеризуется числом (длиной) и направлением. Наглядно его можно представить себе в виде направленного отрезка, хотя, говоря о векторе, правильнее иметь в виду целый класс направленных отрезков, которые все параллельны между собой, имеют одинаковую длину и одинаковое направление (рис. 1). Примерами физических величин, которые имеют векторный характер, могут служить скорость (поступательно движущегося тела), ускорение, сила и др. Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ох, Оу и Oz единичные векторы (орты), обозначаемые i , j , kсоответственно (см. рис. 12).

 

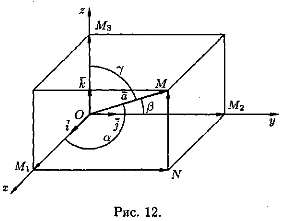
Выберем произвольный вектора пространства и совместим его начало с началом координат: а=ОМ.

Найдем проекции вектора ана координатные оси. Проведем через конец вектораОМ плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через М₁ , М₂ и Мз.Получим прямоугольный параллелепипед, одной из диагоналей которого является векторОМ. Тогда пр _ха=|OM ₁|, np_ya = |ОМ₂|, пр_zа=|ОМз|. По определению суммы нескольких векторов находим а = ОМ ₁ + M₁N + NM.

А так как M ₁N=OM ₂ , NM =ОМз, то

а=ОМ ₁ + ОМ ₂+ ОМ₃                                             (5.1)

 

Обозначим проекции вектораа=ОМ на оси Ох, Оу и Oz соответственно через а_х, а_у и a_z, т.е. |OM₁| = а_х,|ОМ₂| = а_у, |ОМ₃| = а_z. Тогда из равенств (5.1) и (5.2) получаем

a=a_xi+a_yj+a_zk            (5.3)

Эта формула является основной в векторном исчислении и называется разложением вектора по ортам координатных осей. Числа а_х, а_у, a_zназываются координатами вектора а, т. е. координаты вектора есть его проекции на соответствующие координатные оси.

Векторное равенство (5.3) часто записывают в символическом виде: a = (a_x ;a_y ;a_z).

Равенство b = (b_x ;b_y ; b_z ) означает, что b = b_х•i+b _у •j + b_z • k . Зная проекции вектора а, можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать

  

Отсюда

т. е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.

Пусть углы вектора а с осями Ох, Оу и Oz соответственно равны . По свойству проекции вектора на ось, имеем

Или, что то же самое,

Числа   называются направляющими косинусами вектора а.

Подставим выражения (5.5) в равенство (5.4), получаем

Сократив на получим соотношение

т. е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.

Легко заметить, что координатами единичного вектораe являются числа

Итак, задав координаты вектора, всегда можно определить его модуль и направление, т.е. сам вектор.

4) Пусть даны два вектора и , заданные своими проекциями:

или

или 

Укажем действия над этими векторами.

1.Сложение:

т.е. при сложении двух векторов одноимённые координаты складываются.

2.Вычитание:

т.е. при вычитании двух векторов одноимённые координаты вычитаются.

3.Умножение вектора на число:

т.е. при умножении вектора на число все координаты умножаются на это число.

4.Скалярное произведение:

Чтобы выразить скалярное произведение

                              (1)

в координатной форме, предварительно найдём скалярные произведение ортов. По определению,

Итак, скалярное произведение вектора на самого себя равно квадрату длины вектора. В частности,

Так как векторы

попарно перпендикулярны, то

Теперь выполним умножение векторных многочленов:

 

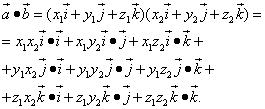
Подставляя в правую часть равенства значения соответствующих скалярных произведений ортов, получим

               (7)

Из соотношений (6) и (7) следует, что длина вектора выражается равенством

5.Угол между двумя векторами

Из (1), (4) и (7) получаем:

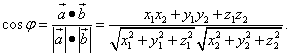
5) Линейные операции над векторами.

 

Определение 5.4. Суммой a + b векторов a и b называется вектор, идущий из начала вектора а в конец вектора b, если начало вектора b совпадает с концом вектора а.

b

a+b

a

 

Замечание. Такое правило сложения векторов называют правилом треугольника.

 

Свойства сложения:

Свойство 1. a + b = b + a.

Доказательство. Приложим векторы а и b к общему началу и рассмотрим параллелограмм

AOBC. Из определения 5.4 и треугольника ОВС следует, что ОС=b+a, а из треугольника

ОАС – ОС=а+b. Свойство 1 доказано.

В а С Замечание. При этом сформулировано еще одно правило

b b сложения векторов – правило параллелограмма: сумма

a+b= векторов a и b есть диагональ параллелограмма, построенно-

=b+a го на них как на сторонах, выходящая из их общего начала.

 

О А

а

Свойство 2. (a+b)+c=a+(b+c).

b Доказательство. Из рисунка видно, что

A a+b B (a+b)+c=(OA+AB)+BC=OB+BC=OC,

a a+(b+c)=OA+(AB+BC)=OA+AC=OC.

Свойство 2 доказано.

b+с

O c С

 

 

 

Свойство 3. Для любого вектора a существует нулевой вектор О такой, что a+О=а.

Доказательство этого свойства следует из определения 5.4.

 

Свойство 4. Для каждого вектора a существует противоположный ему вектор a^/ такой, что а+а^/=О.

Доказательство. Достаточно определить a^/ как вектор, коллинеарный вектору a, имеющий одинаковую с ним длину и противоположное направление.

 

Определение 5.5. Разностью а – b векторов а и b называется такой вектор с, который в сумме с вектором b дает вектор а.

 

a a-b

 

 

b

 

Определение 5.6. Произведением ka вектора а на число k называется вектор b, коллинеарный вектору а, имеющий модуль, равный |k||a|, и направление, совпадающее с направлением а при k>0 и противоположное а при k<0.

 

Свойства умножения вектора на число:

Свойство 1. k(a + b) = ka + kb.

Свойство 2. (k + m)a = ka + ma.

Свойство 3. k(ma) = (km)a.

 

Следствие. Если ненулевые векторы а и b коллинеарны, то существует такое число k, что b = ka.

6) Векторное произведение — это псевдовектор, перпендикулярный плоскости, построенной по двум сомножителям, являющийся результатом бинарной операции «векторное умножение» над векторами в трёхмерном Евклидовом пространстве. Произведение не является ни коммутативным, ни ассоциативным (оно является антикоммутативным) и отличается от скалярного произведения векторов. Во многих задачах инженерии и физики нужно иметь возможность строить вектор, перпендикулярный двум имеющимся — векторное произведение предоставляет эту возможность. Векторное произведение полезно для «измерения» перпендикулярности векторов — длина векторного произведения двух векторов равна произведению их длин, если они перпендикулярны, и уменьшается до нуля, если векторы параллельны либо антипараллельны.

Скаля́рное произведе́ние (в зарубежной литературе - scalar product, dot product, inner product ) — операция над двумя векторами, результатом которой является число (скаляр), не зависящее от системы координат и характеризующее длины векторов-сомножителей и угол между ними. Данной операции соответствует умножение длины вектора x на проекцию вектора y на вектор x. Эта операция обычно рассматривается как коммутативная и линейная по каждому сомножителю.

Нормированные векторы

     Вектор называется нормированным или единичным, если

     Если то соответствующими этому вектору нормированными векторами будут

7) Понятие функции одной переменной

Рассмотрим два числовых множества X и Y. Правило f, по которому каждому числу хI Х ставится в соответствие единственное число yI Y, называется числовой функцией, заданной на множестве Х и принимающей значения во множестве Y.

Таким образом, задать функцию, значит задать три объекта:

1) множество Х (область определения функции);

2) множество Y (область значений функции);

3) правило соответствия f (сама функция).

Например, поставим в соответствие каждому числу его куб. Математически это можно записать формулой y=x³. В этом случае правило f есть возведение числа х в третью степень. В общем случае, если каждому х по правилу f соответствует единственный y, пишут y = f(x). Здесь "х" называют независимой переменной или аргументом, а "y" -зависимой переменной (т.к. выражение типа x³ само по себе не имеет определенного числового значения пока не указано значение х) или функцией от х. О величинах х и y говорят, что они связаны функциональной зависимостью. Зная все значения х и правило f можно найти все значения у. Например, если х=2, то функция f(x) =x³ принимает значение у= f(2) =2³ =8.

Способы задания функции одной переменной

Существуют несколько способов задания функции.

Аналитический способ. Функция f задается в виде формулы y=f(x). Например, y=3cos(x)+2x². Этот способ является преобладающим в математических исследованиях и подробно рассматривается в классическом курсе математики. В географических исследованиях соответствие между переменными величинами x и y не всегда удается записать в виде формулы. Во многих случаях формула бывает неизвестна. Тогда для выражения функциональной зависимости используются другие способы.

 

Графический способ. На метеорологических станциях можно наблюдать работу приборов-самописцев, регистрирующих величины атмосферного давления, температуры воздуха, его влажности в любой момент времени суток. По полученному графику можно определить значения указанных величин в любой момент времени. Графиком функции y=f(x) называется множество всех точек плоскости с координатами (x, f(x)). График содержит всю информацию о функции. Имея перед собой график, мы как бы "видим функцию".

 

Табличный способ. Этот способ является наиболее простым. В одной строке таблицы записываются все значения аргумента (числа), а в другой – значения f(x), соответствующие каждому х. Например, зависимость температуры воздуха (Т) от времени суток (t) в определенный день можно представить таблицей.

 

t	0	1	2	3	4	5	6	7	8	9	10	11
T,0С	12	11	10	9	8	7	8	10	12	14	16	17

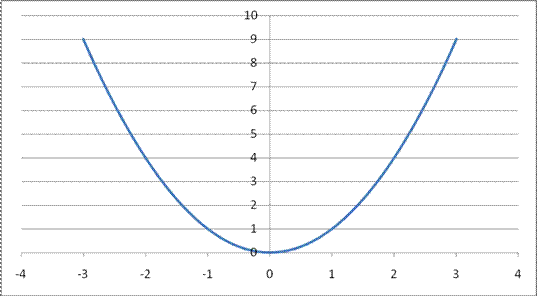
Степенные функции: Функция вида у(х)=хⁿ, где n – число Î R, называется степенной функцией. Число n может принимать раличные значения: как целые, так и дробные, как четные, так и нечетные. В зависимости от этого, степенная функция будет иметь разный вид. Рассмотрим частные случаи, которые являются степенными функциями и отражают основные свойства данного вида кривых в следующем порядке: степенная функция у=х² (функция с четным показателем степени – парабола), степенная функция у=х³ (функция с нечетным показателем степени – кубическая парабола) и функция у=√х (х в степени ½) (функция с дробным показателем степени), функция с отрицательным целым показателем (гипербола). Степенная функция у=х² 1.     D(x)=R – функция определена на все числовой оси; 2.     E(y)=[0;∞) - функция принимает положительные значения на всей области определения; 3.     При х=0 у=0 - функция проходит через начало координат O(0;0). 4.     Функция убывает на промежутке (-∞;0] и возрастает на промежутке [0;∞). 5.     Функция является четной (симметрична относительно оси Оу).

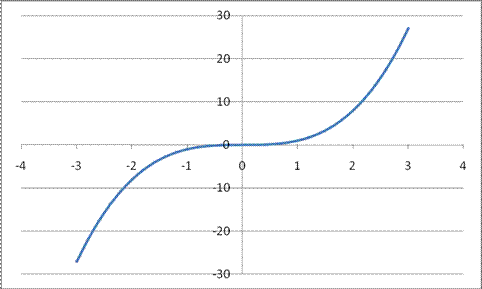
Степенная функция у=х³ 1.     График функции у=х³ называется кубической параболой. Степенная функция у=х³ обладает следующими свойствами: 2.     D(x)=R – функция определена на все числовой оси; 3.     E(y)=(-∞;∞) – функция принимает все значения на своей области определения; 4.     При х=0 у=0 – функция проходит через начало координат O(0;0). 5.     Функция возрастает на всей области определения. 6.     Функция является нечетной (симметрична относительно начала координат).

Степенная функция с целым отрицательным показателем: Если показатель степени n является нечетным, то график такой степенной функции называется гиперболой. Степенная функция с целым отрицательным показателем степени обладает следующими свойствами: 1.     D(x)=(-∞;0)U(0;∞) для любого n; 2.     E(y)=(-∞;0)U(0;∞), если n – нечетное число; E(y)=(0;∞), если n – четное число; 3.     Функция убывает на всей области определения, если n – нечетное число; функция возрастает на промежутке (-∞;0) и убывает на промежутке (0;∞), если n – четное число. 4.     Функция является нечетной (симметрична относительно начала координат), если n – нечетное число; функция является четной, если n – четное число. 5.     Функция проходит через точки (1;1) и (-1;-1), если n – нечетное число и через точки (1;1) и (-1;1), если n – четное число.

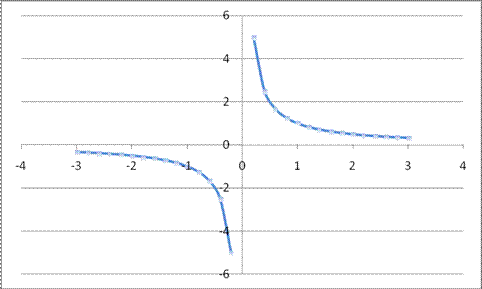
График функции , на интервале x Î [-3;3] Степенная функция с дробным показателем Степенная функция с дробным показателем вида (картинка) имеет график функции, изображенный на рисунке. Степенная функция с дробным показателем степени обладает следующими свойствами: (картинка) 1.     D(x) Î R, если n – нечетное число и D(x)=[0;∞), если n – четное число ; 2.     E(y) Î (-∞;0)U(0;∞), если n – нечетное число; E(y)=[0;∞), если n – четное число; 3.     Функция возрастает на всей области определения для любого числа n. 4.     Функция проходит через начало координат в любом случае.

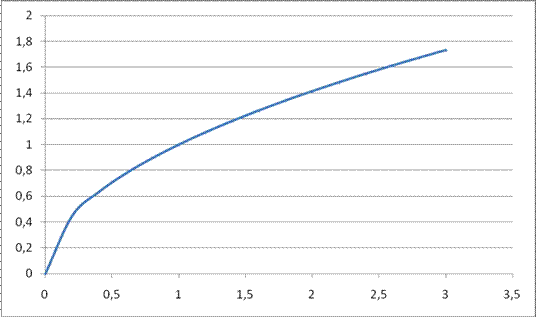
График функции , на интервале x Î [0;3]

График функции , на интервале x Î [0;5]

График функции , на интервале x Î [-3;3] Логарифмические функции: Логарифмическая функция у = log_a x обладает следующими свойствами : 1.     Область определения D(x) Î (0; + ∞). 2.     Область значений E(y) Î ( - ∞; + ∞) 3.     Функция ни четная, ни нечетная (общего вида). 4.     Функция возрастает на промежутке (0; + ∞) при a > 1, убывает на (0; + ∞) при 0 < а < 1. График функции у = log_a x может быть получен из графика функции у = а^х с помощью преобразования симметрии относительно прямой у = х. На рисунке 9 построен график логарифмической функции для а > 1, а на рисунке 10 - для 0 < a < 1.

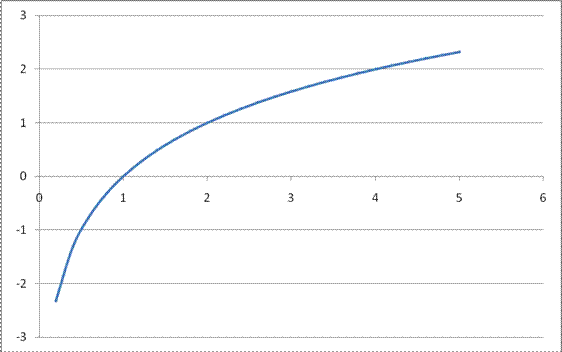
График функции  ; на интервале x Î [0;5]

График функции  ; на интервале x Î [0;5] Тригонометрические функции: Функции y = sin х, у = cos х, у = tg х, у = ctg х называют тригонометрическими функциями. Функции у = sin х, у = tg х, у = ctg х нечетные, а функция у = соs х четная. Функция y = sin (х). 1.     Область определения D(x) Î R. 2.     Область значений  E(y) Î [ - 1; 1]. 3.     Функция периодическая; основной период равен 2π. 4.     Функция нечетная . 5.     Функция возрастает на промежутках [ -π/2 + 2πn; π/2 + 2πn] и убывает на промежутках [ π/2 + 2πn; 3π/2 + 2πn], n Î Z.

График функции у = sin (х)

График функции  ; на интервале x Î [-2 ;2 ] Функция y = cos(х). 1.     Область определения D(x) Î R. 2.     Область значений E(y) Î [ - 1; 1]. 3.     Функция периодическая с основным периодом 2π. 4.     Функция четная. 5.     Функция убывает на промежутках [2πn; π+ 2πn] и возрастает на промежутках [-π+ 2πn; 2πn], nπZ. График функции у = соs (х)

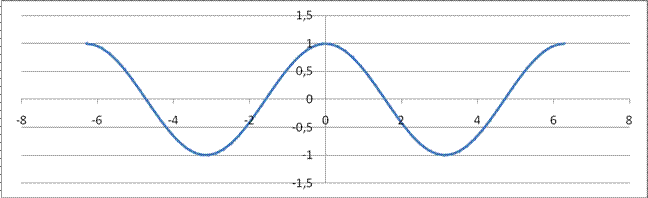
График функции  ; на интервале x Î [-2 ;2 ] Функция y = tg х. 1.     Область определения: D(x) Ï π/2 + πk, kÎZ. 2.     Область значений E(y) Î (- ∞; + ∞) 3.     π- основной период функции. 4.     Функция нечетная. 5.     Функция возрастает на промежутках ( -π/2 +πn;π/2 +πn). График функции у = tg х

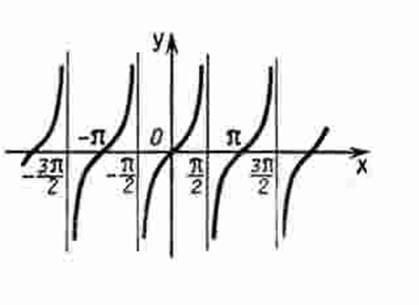
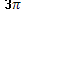График функции  ; на интервале x Î (- ; ) Функция y = ctg х. 1.     Область определения функции: D(x) Ï  xπ/2 +πk, kÎZ. 2.     Область значений функции E(y) Î (- ∞; + ∞). 3.     Функция периодическая с основным периодом π. 4.     Функция нечетная. 5.     Функция у = ctg х убывает на промежутках (πn;π+πn). График функции у = ctg х

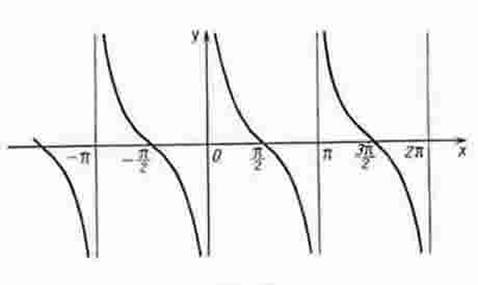
График функции  ; на интервале x Î (-𝜋;) Обратные тригонометрические функции: Функции y = arcsin (х), у = arccos (х), у = arctg (х), у = arcctg (х) называют обратными тригонометрическими функциями. Функция y = arcsin ( x ): Свойства функции y = arcsin (x): 1. Область определения D(x)Î[−1;1] 2. Область значения  E(y)Î [−π/2;π/2] 3. y=arcsin(x)- непрерывная строговозрастающая функция на D 5. График y = arcsin(x) симметричен графику y = sin(x) относительно линии y=x 6. y=arcsin(x) нечетная функция т.е. ∀x∈[−1;1] arcsin(−x)=−arcsin(х) График функции y = arcsin (x)

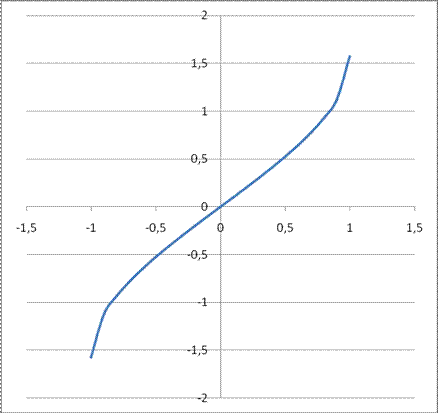
График функции  ; на интервале x Î [- ;] Функция y = arccos ( x ): Свойства функции y = arccos (x): 1. Область определения D(x)Î[−1;1] 2. Область значения  E(y)Î [0;π] 3. y=arccos(x)- непрерывная строговозрастающая функция на D 5. График y = arccos(x) симметричен графику y = cos(x) относительно линии y=x 6. y=arccos(x) функция общего вида График функции y = arccos (x) 

8) Числовая последовательность — это последовательность элементов числового пространства.

Числовые последовательности являются одним из основных объектов рассмотрения в математическом анализе.

Пусть множество — это либо множество вещественных чисел , либо множество комплексных чисел . Тогда последовательность элементов множества называется числовой последовательностью.