15.Метод Зёйделя

Метод Зейделя (иногда называемый методом Гаусса-Зейделя) является модификацией метода простой итерации, заключающейся в том, что при вычислении очередного приближения x(k+1) (см. формулы (1.13),(1.14)) его уже полученные компоненты x(k+1)(k+1) сразу же используются для вычисления x(i+1)(k+1).

В координатной форме записи метод Зейделя имеет вид:

x1(k+1) = c11x1(k) + c12x2(k) + c1n-1xn-1(k) +... + c1nxn(k) + d1

x2(k+1) = c21x1(k+1) + c22x2(k) + c2n-1xn-1(k) + ... + c2nxn(k) + d2

...

xn(k+1) = cn1x1(k+1) + cn2x2(k+1) + cnn-1xn-1(k+1) + ... + cnnxn(k) + dn

где x(0) - некоторое начальное приближение к решению.

Таким образом i-тая компонента (k+1)-го приближения вычисляется по формуле

xi(k+1) = åj=1i-1 cijxj(k+1) + å nj=i cijxj(k) + di , i = 1, ..., n (1.20)

Условие окончания итерационного процесса Зейделя при достижении точности e в упрощенной форме имеет вид:

|| x (k+1) - x (k) || ≤ e.

Существует более точное условие окончания итерационного процесса, которое более сложно и требует дополнительных вычислений

15.Метод прогонки

Для решения систем A x = b с трехдиагональной матрицей наиболее часто применяется метод прогонки, являющийся адаптацией метода Гаусса к этому случаю.

Запишем систему уравнений

d1x1 + e1x2 = b1

c2x1 + d2x2 + e2x3 = b2

c3x2 + d3x3 + e3x4 = b3

... ... ...

cn-1xn-2 + dn-1xn-1+en-1xn= bn-1

cnxn-1 + dnxn = bn

в матричном виде: A x = b где

A=

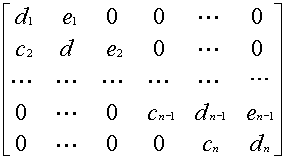
Выпишем формулы метода прогонки в порядке их применения.

Прямой ход метода прогонки (вычисление вспомогательных величин): a2 = -e1 / d1

b2 = b1 / d1

ai+1 = -ei / [di + ciai], i=2, ..., n-1

bi+1 = [-cibi + bi] / [di + ciai], i=2, ..., n-1 (1.9)

Обратный ход метода прогонки (нахождение решения): xn = [-cn bn + bn] / [dn + cnan]

xi = ai+1 xi+1 + bi+1, i = n-1, ..., 1 (1.10)

Метод прогонки можно применять, если нигде в формулах знаменатели не равны нулю. В [2, стр.134] доказано следующее

УТВЕРЖДЕНИЕ 1.1 Для применимости формул метода прогонки достаточно выполнения условий диагонального преобладания у матрицы A, то есть

| di | ≥ | c i | + | ei |

причем хотя бы одно неравенство должно быть строгим.

16.Метод обратной итерации.

Рассмотрим квадратную матрицу A. Для простоты считаем ее самосопряженной невырожденной матрицей, среди собственных значений которой нет кратных. Выбираем действительный параметр b. Матрицы A и A – bE имеют общую систему собственных векторов. Если xk — собственный вектор матрицы A, то верно равенство

Введем обозначение Рассмотрим последовательность равенств Применим степенной алгоритм для нахождения максимального по абсолютной величине собственного числа матрицы B. Мы уже знаем, что он сойдется. Таким образом, мы можем найти собственное число матрицы A, наиболее близкое к b.

Схема метода, таким образом, есть.

1. Фиксируем параметр b (для определения нижней границы спектра, очевидно, необходимо положить b = 0).

2. Фиксируем произвольный ненулевой вектор

3. Решаем систему линейных уравнений

Это и есть обратная итерация.

После того, как найдена последовательность векторов, считаем

Таким образом, мы можем найти собственное число матрицы, ближайшее к b.

Очевидно, что проблема поиска собственного числа матрицы, ближайшего к данному, является вычислительно гораздо более «дорогой» задачей, чем вычисление максимального по абсолютной величине собственного числа.