Критерий Найквиста-Михайлова.
Этот критерий позволяет судить об устойчивости замкнутой системы по АФХ разомкнутой системы.
Представим АФХ разомкнутой системы в виде: W(p)=A(p)/D(p), тогда замкнутая система
Ф(р)=1+А(р)/D(p)=A(p)/Д(р).
В частотном плане имеем D(jw) и Д(jw) – годографы хар-го ур-ия разомкнутой и замкнутой систем соответственно. Для док-ва критерия введем вспом. частотную ф-цию f(jw)=1+w(jw)=Д(jw)/D(jw). Рассмотримдок-во для статических систем, при условии, что разомкнутая системаустойчива, т.е. состоит из уст-х звеньев. В этом сл-е согласно критерию Михайлова, кот-ый справедлив и для разомкнутых систем. Приращение годографа разомкнут системы, так же, как и приращение замкн.системы , т.к степень Д(jw) совпадает со степенью D(jw)=> суммарное приращение арг.частотной кривой f(jw) равно разности приращения аргументов числителя и знаменателя т.е. равно нулю=>чтобы кривая f(jw) не имело пол-ых корней, должна охватывать начало координат, от вспомог-ой кривой f(jw) легко перейти к w(jw) очевидно, что для того чтобы не было пол-ых действительных корней, кривая w(jw) не должна охватывать т. с координатами (-1;j0).
Использование критерия Н-М для астатических систем затрудняется тем, что АФХ начинаются из бесконечности, т.к. каждый интегратор добавляет отрицат. фазовый сдвиг –pi/2. След-но замкнуть АФХ можно дугой бесконечно большого радиуса, причем замыкают АФХ на полож-ую действ.ось с углом ν*pi/2, где ν – порядок астатизма.
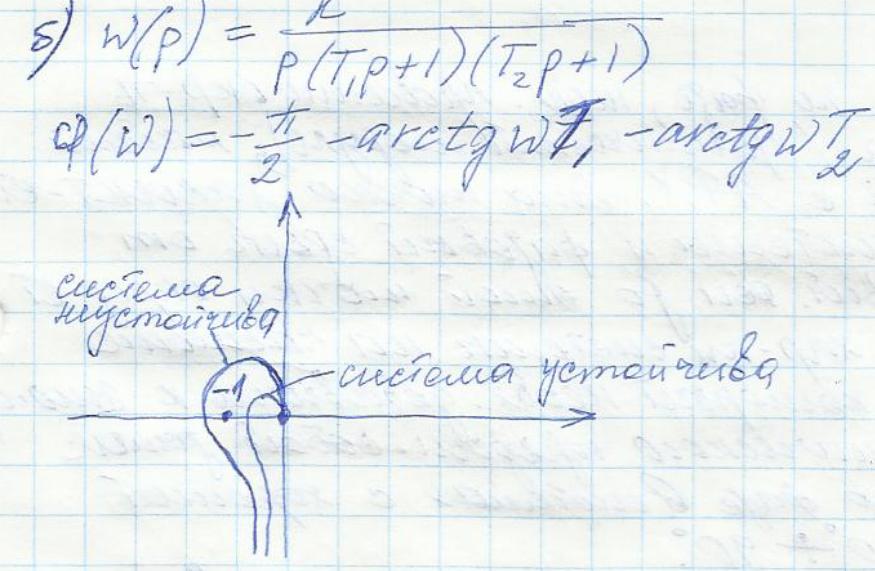
25.Понятие запаса по фазе и амплитуде
Д
ля
устойчивости системы достаточно чтобы
годограф не охватывал критическую точку
с координатами(-1,0).Однако для нормального
функционирования системы годограф
должен быть удален на определенное
расстояние от критической точки. Поэтому
в ТАУ введены понятия запаса системы
по фазе и амплитуде. Запас по фазе
определяется по критической амплитуде.
А запас по амплитуде определяет запас
при критической фазе системы –π. Покажем
на АФХ способ определения этих запасов.
Чтобы найти запас по фазе необходимо провести окружность единичного радиуса (критический модуль), найти точку пересечения с АФХ. Эта точка характеризует частоту среза системы, и фазовый сдвиг от положительной действительной оси до этой точки определяет значение фазовой характеристики системы на частоте среза. Тогда угол, который необходимо добавить к этому значению до критического –π представляет собой запас по фазе. Запас по фазе в системах с хорошей динамикой γ=30÷90°. Чем выше запас по фазе, тем меньше величина перерегулирования переходной характеристики замкнутой системы.
Запас по амплитуде определяется как величина от точки пересечения АФХ отрицательной действительной оси до значения -1(критическая точка). Запас по амплитуде всегда выполняется в линейной непрерывной системе.
26.Логарифмический критерий устойчивости
О
н
по сути дела является переносом критерия
Найквиста-Михайлова на логарифмические
характеристики разомкнутой системы.
Как известно в МЧХ рассматривается
отдельно модуль АФХ и ее аргумент. Причем
частоты явно присутствуют в графике и
если расположить ЛФЧХ непосредственно
под ЛАЧХ под тем масштабом частот, то
запас по фазе можно определить, опуская
перпендикуляр из частоты
, т.е. точке пересечения этого перпендикуляра
с фазовой характеристикой будет найдена
собственная фаза системы и не составляет
труда определиться с запасом по фазе.
Определиться с запасом по амплитуде
можно, восстановив перпендикуляр из
точки пересечения фазовой характеристики
и критического значения. Пересечение
этого перпендикуляра даст участок до
оси частот, представляющий собой запас
по амплитуде. Рассмотрим в общем виде
примеры устойчивой и неустойчивой
системы. Отметим, что в устойчивой
системе всегда
<
