4.Уравнения типовых звеньев автоматики.

Уравнение элемента – дифференциальное или алгебраическое уравнение, связывающее между собой выходную(y(t)) и входную(x(t)) величину элемента. Для основных элементов такое описание имеется и сводится к типовым линейным уравнениям 1 порядка. При записи уравнений слева от равно записывается выходная величина со всеми преобразованиями, справа – входная.

1.Алгебраическое уравнение Y(t)=kX(t)

Описывает маломощный электрический усилитель, датчики, механические передачи. Типовое звено – безъинерционное, К – статический коэффициент передачи.

2. Дифференциальное уравнение 1 порядка.

Это уравнение может иметь производную по входной или выходной величинам, рассм. Наличие по выходной величине: a Стандартная запись в ТАУ осуществляется таким образом, что коэффициент при y(t)<1. В результате получим уравнение:

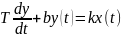,Т – постоянная времени. Такое уравнение имеет типовое инерционное звено 1 порядка. Частные случаи:А). Т=0 – безъинерционное звено.Б). Коэффициент при Y(t)=0 , - идеальный интегратор, таким звеном можно описать интегрирующий операционный усилитель или двигатель, работающий с постоянным вращающим моментом. Если присутствует производная входного сигнала

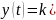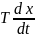+ ) – форсирующее звено. Частные случаи:Б1).Т=0 – безъинерционное звено.Б2).Коэффициент при x(t)=0 , – идеальный дифференциатор. Если в уравнении присутствует производная входного сигнала, то звено обладает форсирующими свойствами. В). Производная на двух сигналах + 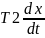) – инерционно – форсирующее звено. Возможно 2 случая:Т1>T2 В этом случае в звене преобладают дифференционные свойства, если наоборот – форсирующие.Если коэффициент при Y(t)=0 – изодромное звено. Если коэффициент при х(t)=0 – реальный дифференциатор.

3. Дифференциальное уравнение 2 порядка.

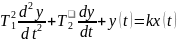1.)Если Т2>T1 – корни характерестического уравнения отрицательные и действительные, описывает типовое инерционное звено 2ого порядка. Такими звеньями описываются все мощные инерционные устройства эл-магн типа, когда учитывается эл-магн постоянная времени. Если Y(t)=0 – уравнение интегратора с инерционностью. 2).Если 2Т1>T2 – корни уравнения комплексно сопряженные с отрицательной вещественной частью. 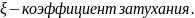, 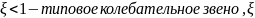=0 – типовое консервативное звено.

4. В отдельных системах автоматики(передача топлива по трубам, звука по длинным линиям) возникают задержки – звено чистого запаздывания. Т

5.Передаточные функции типовых звеньев.

Для описания динамических свойств в ТАУ используют понятие передаточных функций. Для их получения используют преобразование Лапласа, для чего преобразуют линейное уравнение элемента таким образом , что функция времени преобразуется в функцию f(p) комплексного оператора Р. L{f(t)}=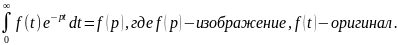 Также существует обратное преобразование, чтобы по изображению можно получить оригинал. Передаточная функция – отношение изображения выходной величины к изображению входной величины при нулевых начальных условиях W(p)=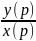

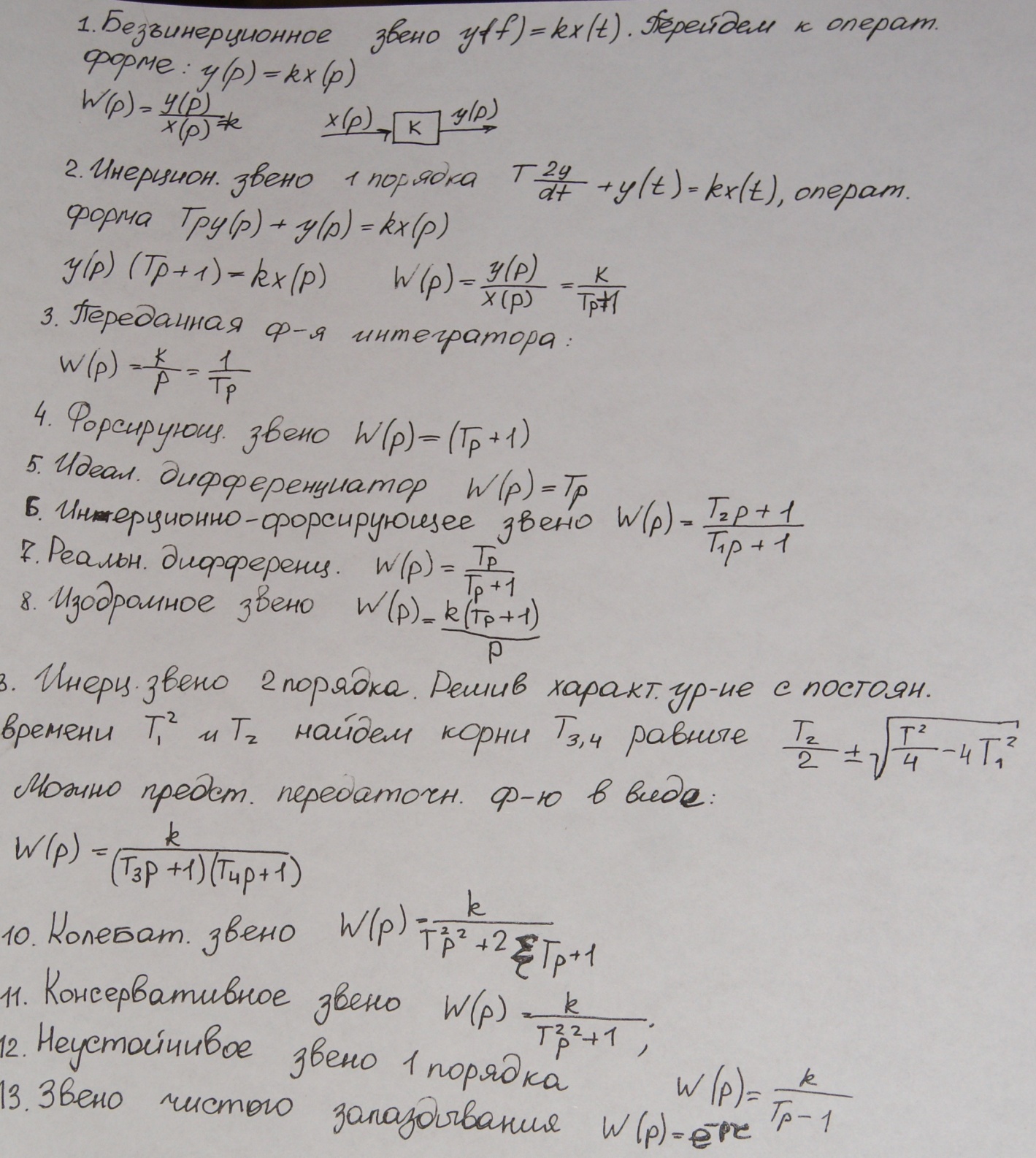
6. Функциональные и структурные схемы.

Функциональная схема – схема в которой каждому функциональному элементу соответствует определенное звено. Структурная – схема, в которой математическим описаниям каждого функционального блока соответствует определенное звено, т.е. в структурной схеме каждое звено может содержать уравнение связывающее входную и выходную величину или передаточную функцию.

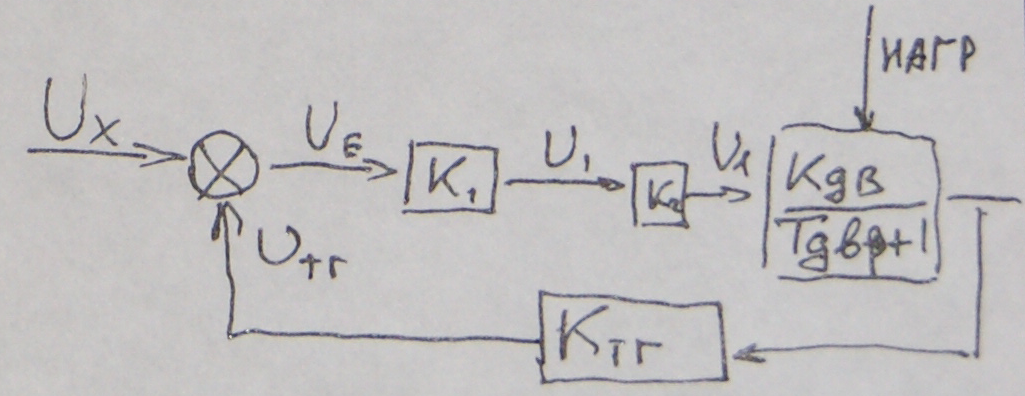
Схема стабилизации частоты вращения двигателя.

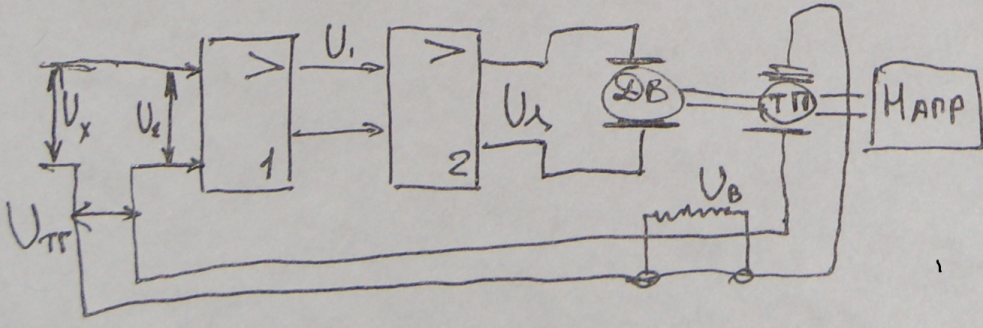
Система содержит предварительный усилитель 1, усилитель мощности 2, на выходе которого напряжение для управления двигателем на обмотке якоря U_я двигатель Дв, на валу которого закреплена нагрузка Нагр. В качестве датчика обратной связи используется тахагенератор, закрепленный на валу двигателя, на выходе которого напряжение U_тг пропорционально частоте вращения двигателя. На вход подается сигнал U_х из которого вычитается U_тг, образуя сигнал рассогласования U_λ .Устройство, которое производит вычисление ε(t) – измеритель рассогласования. Если известна величина нагрузки, по ней можно выбрать по мощности двигатель. По механическим характеристикам двигателя можно найти U_λ0 которое гарантирует частоту ω₀ на выходе двигателя. По статическому коэффициенту передачи усилителя мощности можно найти напряжение U₁ и величину U_ε0,гарантирующего ω₀. По заданной частоте вращения подбираем тахагенератор и по его характеристикам ищем U_тг0.Из уравнения измерителя рассогласования

U_ε= U_х- U_тг, при известных U_ε0 и U_тг0 найдем U_х0., такой входной сигнал необходимо подать на систему чтобы обеспечить частоту ω₀.Пусть выбран двигатель небольшой мощности, усилитель мощности, предварительный усилитель, все датчики – безъинерционные. Запишем уравнения выбранных элементов:1).Измеритель рассогласования U_ε= U_х- U_тг 2).Предварительный усилитель 1 U₁= U_εК₁ 3).Усилитель мощности U_λ= U₁К₂

4).Двигателя Т_дв K_дв U_λ 5). Тахагенератор U_тг = ωК_тг

Переходя к операторной форме можно получить передаточные функции

1). U_ε(р)= U_х(р)- U_тг(р) 2).W₁(р)=K₁ 3).W₂(р)=K₂ 4).W_дв(р)=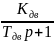 5).W_тг(р)=K_тг