23.Особенности угловых измерений в триангуляции.

На качество угловых измерений в триангуляции на территории городов и строительных площадок влияют следующие факторы:

1)наличие своеобразного микроклимата: транспортные средства, промышленные и энергетические предприятия выделяют в атмосферу тепло, дым, пыль; происходит изменение режима теплопроводности, испарения, конденсации водяного пара от поверхности дорог (с асфальтированным и другим покрытием), железобетонных и металлических конструкций;

2. наличие препятствий для визирного луча теодолита;

3. короткие стороны и резкий перепад уровней высоты;

2. вибрация промышленных зданий, на которых располагаются пункты триангуляции;

5)боковая рефракция.

Местные поля рефракции изменяются во времени и в пространстве, кроме этого, суточные и сезонные изменения боковой рефракции различные. Чтобы уменьшить влияние боковой рефракции на результаты угловых измерений, рекомендуется производить измерения ранней весной или поздней осенью, а в пределах суток - в утреннюю и вечернюю видимость.

В связи с короткими длинами сторон необходимо особое внимание уделять центрированию теодолита и визирных целей.

Поправка за центрировку с" в измеренное направление равна

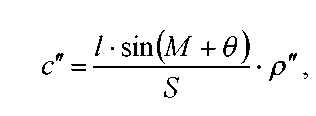
где l - величина линейной редукции; θ - угловой элемент редукции; S-длина стороны; М- измеренное направление.

Поправка за центрировку в измеренный угол с₀'' будет равна

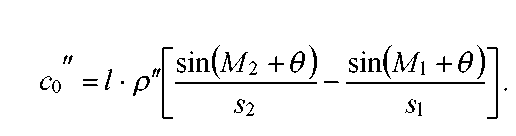
Для трех направлений при равных между собой длинах линий, получим

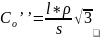
Отсюда найдем линейную редукцию

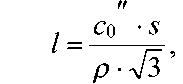
продифференцируем полученное выражение и перейдем к средней квадратической погрешности линейной редукции

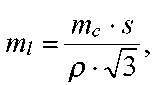
приняв во внимание условие m_c=0.1m_β, получим

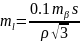
Для определения элементов центрирования и редуцирования в инженерных сетях используют только аналитический метод.

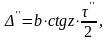
где b - наклон горизонтальной оси в полуделениях уровня, z - зенитное расстояние, 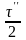- цена полуделений уровня.

При больших углах наклона используют накладной уровень по концам пузырька которого берут отсчёты, рассчитывают и вводят поправки в измеренное горизонтальное направление.

24.Трилатерационные сети. Типовые схемы сетей.

Метод трилатерации применяют для построения инженерно-геодезических сетей 3 и 4 класса, а также сетей сгущения 1 и 2 разрядов различного назначения. Сети трилатерации для решения инженерно-геодезических задач строят в виде свободных сетей, состоящих из отдельных фигур: геодезиче­ских четырехугольников, центральных систем или их комбинаций с треугольниками.

Типовой фигурой трилатерации является треугольник с измеренными сторонам

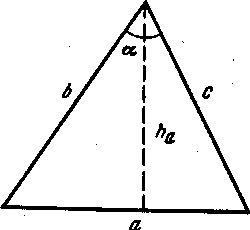
Средняя квадратическая погрешность вычисленного угла может быть определена по формуле

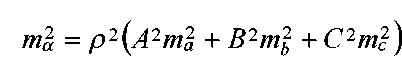(38)

где - средние квадратические погрешности измерения сторон;

а коэффициенты А, В и С находят так:

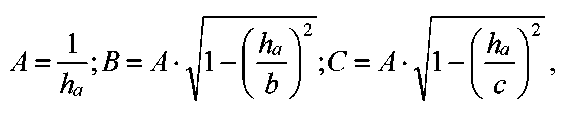
где - высота треугольника, опущенная из вершины на сторону а.

Для линейно протяженных объектов сеть трилатерации создают из цепочки треугольников. Недостатки такого построения состоят в следую­щем:

1. поперечный сдвиг ряда существенно превышает продольный;

1. отсутствие полевого контроля качества измерений для каждой фигуры (при любых погрешностях измерений длин сторон сумма вычисленных углов всегда равна 180°).

При оценке ожидаемой точности ряда равносторонних треугольни­ков трилатерации используют формулы:

а) для продольного сдвига

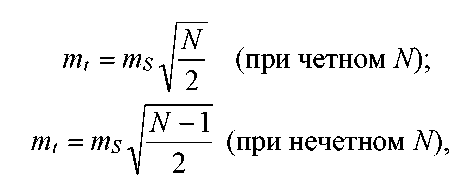
т₈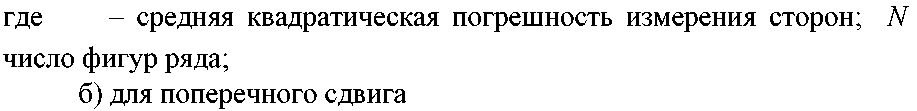

где - порядковый номер связующей стороны;

в) для дирекционного угла связующей стороны

(41)

где - длина сторон треугольников.

Чтобы исключить второй недостаток, сети трилатерации на практике развивают в виде геодезических четырехугольников. В каждом геодезиче­ском четырехугольнике измеряется шесть сторон, причем одна из них (лю­бая) является избыточной и может быть вычислена, используя результаты измерений других сторон. Это может служить полевым контролем качест­ва измерений длин линий. Кроме того, геодезический четырехугольник яв­ляется более жесткой фигурой, чем ряд составленный из таких фигур, и обладает более высокой точностью.

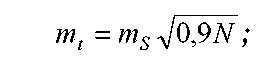
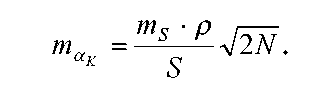
Оценка точности ряда геодезических четырехугольников, состояще­го из квадратов и уравненного за условия фигур, может быть выполнена по следующим формулам: