47. Действие магнитного поля на проводники с током и движущиеся заряды.

Закон, определяющий магнитную часть силы Лоренца, действующую на движущийся точечный заряд в магнитном поле, получен обобщением опытных фактов. Он выражается формулой , где вектор не зависит от величины заряда и его движения, — угол между векторами и . Он характеризует только магнитное поле и называется магнитной индукцией. Вектор силы перпендикулярен как вектору , так и вектору . Эта формула указывает принципиальный способ измерения магнитного поля .

Умножая это соотношение векторно на и принимая во внимание, что , получим . Отсюда вектор определяется однозначно. В системе СИ магнитная индукция измеряется в Тл (тесла).

Так как на заряд действует также электрическое поле, то две силы можно объединить: .

Опыты по действию магнитного поля на движущиеся заряды проще производить не с отдельными зарядами, а с электрическими токами. Допустим, что ток создается движением одинаковых частиц с зарядом и концентрацией . Тогда . Число частиц в объеме будет , а сила, действующая в магнитном поле этот объем равна: 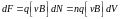, или .

Это выражение верно и в общем случае, когда носителями являются разные заряды.

Пусть теперь ток течет вдоль тонкого провода с площадью сечения . Выделим теперь бесконечно короткий участок провода 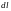и вычислим действующую на него силу. Так как , то , или , причем направление вектора совпадает с направлением тока. Вектор называется объемным, а — линейным элементом тока. Получаем окончательно .

Эта формула определяет силу, действующую в магнитном поле на линейный элемент тока и называется законом Ампера. Сила, действующая на провод конечной длины, получается интегрированием по всей длине провода:

.

48-49. Магнитное поле равномерно движущегося заряда. Закон Био—Савара. Поле длинного прямого провода, кругового витка.

Токи и движущиеся точечные заряды сами создают магнитное поле.

Начнем с движущегося точечного заряда , ограничиваясь при этом равномерными движениями с малыми скоростями. Такой закон является обобщением опытных фактов и выражается формулой , где — радиус-вектор, проведенный от заряда к точке наблюдения, — скорость движения частицы, — магнитная пост.

К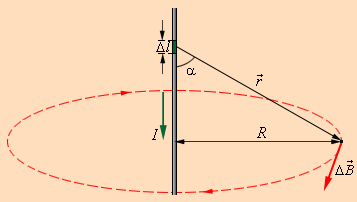 ак и в случае закона Ампера, можно перейти от одного движущегося заряда к току. Вычисления приводят к формуле .

Эта формула выражает закон Био—Савара. Полное поле получается интегрированием этой формулы по всем токам . Эти выражения применимы только для постоянных токов.

С помощью этого закона можно получить конечные формулы для некоторых проводников.

1. Бесконечный прямолинейный провод, по которому течет ток . Интегрирование формулы приводит к результату , где — расстояние от точки наблюдения до проводника с током.

Если расположить рядом два параллельных тока, то один ток создает в месте, где находится другой, то можно вычислить силу, с которой первый ток действует на участок второго тока длиной : , где — расстояние между токами. Токи, текущие в одном направлении, притягиваются, а в противоположных — отталкиваются. Эта формула позволяет ввести единицу тока ампер. Если токи по 1 А, , то сила должна быть .

2. Индукция магнитного поля кругового тока в центре приводит к формуле , где — радиус кругового тока. Кроме вектора магнитной индукции вектор напряженности магнитного поля . В вакууме оба вектора связаны простой формулой .

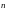Для витка с током можно также ввести понятия ие магнитного момента, по аналогии с электрическим дипольным моментов. Вектор магнитного момента произвольного контура с током равен , где — площадь витка, — единичный вектор нормали к плоскости витка. Если вращать ток в направлении его движения, то вектор нормали показывает направление вкручивания правого винта. Для круглого витка можно записать .